Разряд конденсатора на цепь с резистором и катушкой

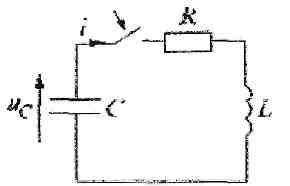
Рис. 12.1

Пусть в цепи, изображенной на рис. 12.1, конденсатор был заряжен до напряжения u_C (0-) = Uo. Исследуем процессы в контуре, образованном резистором, конденсатором и катушкой после замыкания в момент t = 0 ключа. Так как источники в цепи отсутствуют, то установившиеся составляющие решений равны нулю. Решение будет состоять из одной свободной составляющей.

Составление характеристического уравнения. Определение собственных частот цепи.

По второму закону Кирхгофа t ≥ 0 имеем:

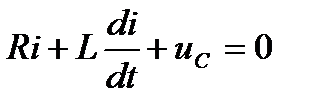
Учитывая, что 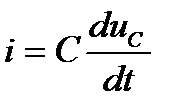, получаем дифференциальное уравнение второго порядка для свободной составляющей напряжения.

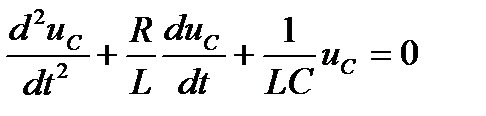
Характеристическое уравнение при этом имеет вид:

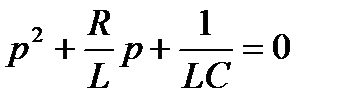
Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения

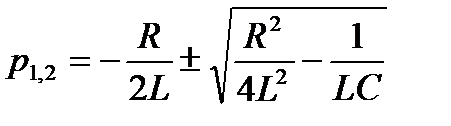
В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений.