СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ И МИКРОПРОГРАММ

Наиболее наглядно изображать микропрограммы и алгоритмы в виде ориентированного графа, т.н. граф схемы алгоритма (ГСА). Кроме наглядности это дает возможность использовать для анализа и преобразования микропрограмм эффективные методы теории графов. При графическом описании отдельные функции алгоритмов (микрооперации) отображаются в виде условных графических изображений, т.н. вершин. В ГСА обычно используют вершины следующих типов:

- вершина «начало» имеет один выход, входов не имеет. Обозначает начало микропрограммы.

- вершина «конец» имеет любое число входов, выходов не имеет. Обозначает конец микропрограммы.

- операторная вершина имеет любое число входов, один выход. Внутри операторной вершины записывается одна микрокоманда - совокупность микроопераций, допускающих совместное (т.е. одновременное) выполнение.

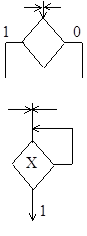
- условная вершина имеет любое число входов и 2 выхода. Внутри условной вершины записывается булевое выражение, в зависимости от значения которого осуществляется выбор направления дальнейшего выполнения микропрограммы.

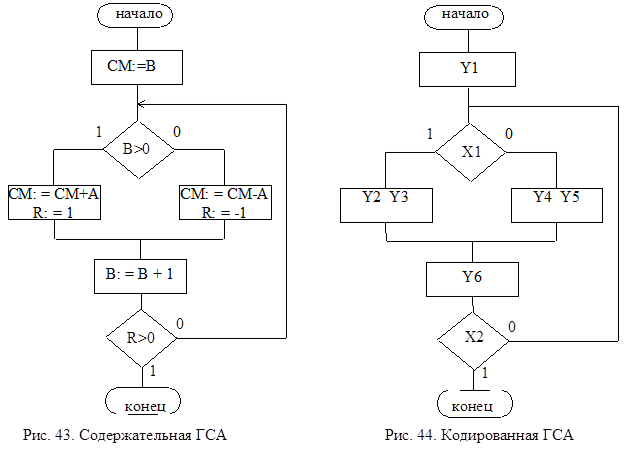
- особый вид условной вершины - ждущая - имеет множество входов, 2 выхода, 1 из которых заведен на вход. При попадании в ждущую вершину выход из нее возможен только при выполнении условия Х.

Граф микропрограммы состоит из совокупности перечисленных вершин и дуг, соединяющих выходы одних вершин с входами других. Соединение вершин и направление дуг графа определяют исходя из алгоритма операции, описываемого графом, и структуры операционного автомата.

Сама микропрограмма и ее граф должны быть корректны, т.е. отвечать следующим условиям:

1. В графе должна быть только одна начальная и одна конечная вершина.

2. В любую вершину графа должен вести по крайней мере один путь из начальной вершины.

3. Из каждого выхода любой вершины графа должен существовать по

крайней мере один путь в конечную вершину.

4. При всех возможных значениях логических условий и используемых слов должен существовать путь из начальной вершины в конечную.

Пример ГСА представлен на рисунке:

ГСА на рис.43 называется содержательной, т.к. внутри вершин записаны в явном виде микрооперации и логические условия. Если же каждую микрооперацию обозначить символами Yi, a логические условия через Xi, то получится так называемая кодированная ГСА (рис.44 ). Для правильного восприятия микропрограммы, заданной в виде кодированной ГСА, необходимо знать соответствия между Yi, Xi и содержанием соответствующих микроопераций и логических условий.

Для записи микроопераций внутри вершин используется так называемый Ф-язык. Подробно с зтим языком можно ознакомиться в последующих курсах «Схемотехника ЭВМ», «Теория и проектирование ЭВМ». Здесь же мы рассмотрим только основные положения этого языка.

В этом языке существуют двоичные константы и переменные: 0010 - константа, A(1:4) - четырехразрядное слово - четырехразрядная двоичная переменная. Например, A(1:4)=1010 означает, что в первом разряде слова A будет 1, во втором - 0 и т.д. A(2:3) - часть слова A, размещенная во втором и третьем разрядах.

Наиболее употребительные операции Ф-языка:

присваивание - A( 0:3 ): = 1000, B( 1:4 ): = A( 5:8 ) и т.д.

инвертирование - A( 0:3 ): = ^ B( 1:4 )

конкатенации - С( 0:6 ): = A( 0:3 ). B( 1:3 )

Пример 1. A( 0:3 ): = 1100 B( 1:4 ): = A( 0:3 ) ® B( 1:4 ): = 1100

2. B( 1:4 ): = 0101 A( 0:3 ): = ^B( 1:4 ) ® A( 0:3 ): = 1010

3. A( 0:3 ): = 1101 B( 1:3 ): = 110 C( 0:6 ): = A( 0:3 ). B( 1:3 ) ® C(0:6):=1101110

Запись вида A(2) означает, что здесь рассматривается второй разряд слова A, т.е. это бит, записанный во втором разряде слова A.

При выполнении операций присваивания необходимо соблюдать равенство разрядов в словах слева и справа от знака присваивания. Операции сложения, логического сложения и т.д. в Ф-языке записываются обычным способом через оператор присваивания:

C(0:n):=A(0:n)+B(0:n)

D(0:n):=A(0:n)vB(0:n) и т.д.