Недостаток рассматриваемого способа в том, что в цепь распространения сигнала вносится дополнительная задержка, что не всегда допустимо.
Схема с использованием дублирования перегружаемого элемента представлена на рис.7.в. Количество p дополнительных элементов, выполняющих ту же функцию, что и К-тый элемент, определяется по формуле:
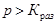
При таком способе обеспечения 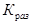 дополнительная задержка не вносится, но увеличивается нагрузка на элементы, формирующие сигналы
дополнительная задержка не вносится, но увеличивается нагрузка на элементы, формирующие сигналы 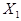 и
и 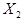 , что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного Краз.
, что может привести к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного Краз.
1.5. СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЯ НА 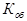 .
.
Представлению функции в виде ДНФ соответствует двухуровневая КС (если считать, что на ее вход могут поступать как прямые так и инверсные входные сигналы), на первом уровне которой элементы И , а их выходы объединяются на втором уровне элементом ИЛИ . Такое построение КС обеспечивает ее максимальное быстродействие, так как ранг схемы минимален. Однако, не всегда возможно на первом уровне и, особенно, на втором выбрать логические элементы с требуемым 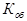 , т.к. может оказаться, что ЛЭ с таким
, т.к. может оказаться, что ЛЭ с таким 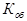 не выпускаются промышленностью. В этом случае необходимо с помощью нескольких элементов с меньшим
не выпускаются промышленностью. В этом случае необходимо с помощью нескольких элементов с меньшим 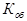 получить эквивалент с большим
получить эквивалент с большим 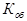 либо, что предпочтительней, преобразовать БФ, перейдя от ДНФ к скобочной форме. Этот переход сопровождается уменьшением
либо, что предпочтительней, преобразовать БФ, перейдя от ДНФ к скобочной форме. Этот переход сопровождается уменьшением 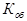 логических элементов, требуемого для построения схемы. Осуществить такой переход можно с помощью факторного алгоритма, суть которого рассмотрим на примере.
логических элементов, требуемого для построения схемы. Осуществить такой переход можно с помощью факторного алгоритма, суть которого рассмотрим на примере.
Пусть задана некоторая булева функция в виде
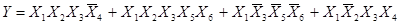
Для реализации этой функции по приведенному выражению необходимо использовать 3 логических элемента 4И, один логический элемент 5И, один логический элемент 4ИЛИ.
С помощью факторного алгоритма получим скобочную форму для заданной функции. Для этого обозначим все конъюнкции буквами:
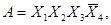
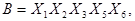
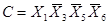
и будем рассматривать их как некоторые множества. Находим попарные пересечения множеств:
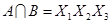 ,
, 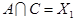 ,
, 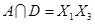 ,
, 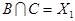 ,
, 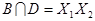 ,
, 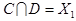 .
.
Полученные пересечения показывают общие части отдельных конъюнкций. Выбираем пересечение, которое имеет наибольшую длину (если такое отсутствует, то выбирают то, которое чаще всего встречается). В данном случае это 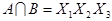 . Поэтому из конъюнкций А и В выносим общую часть
. Поэтому из конъюнкций А и В выносим общую часть 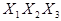 . Тогда имеем:
. Тогда имеем:
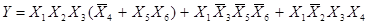 .
.
Обозначим F = 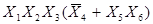 и находим пересечения:
и находим пересечения:
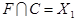 ,
, 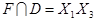 ,
, 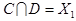 .
.
Следовательно, для исходной функции имеем:
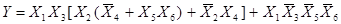 .
.
Обозначим 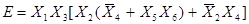 ,
,
Пересечение 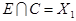 . Следовательно, окончательно имеем:
. Следовательно, окончательно имеем:
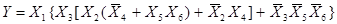
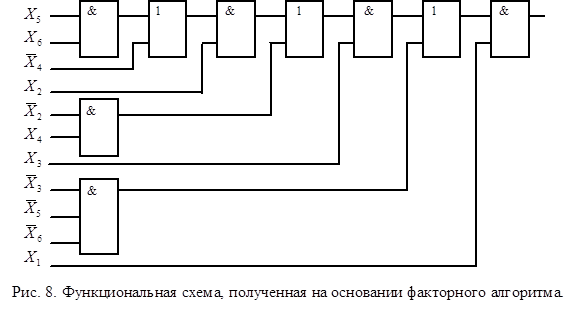
|
Для реализации функции по последнему выражению необходимо 5 элементов 2И, 1 элемент 3И, 3 элемента 2ИЛИ ( рис.8 ).
Как видно из полученной схемы для ее реализации необходимы элементы с 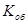 = 2 или 3 (в отличие от исходной с
= 2 или 3 (в отличие от исходной с 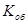 = 4 или 5). Однако ранг схемы увеличился до 7, что приводит к увеличению задержки срабатывания схемы.
= 4 или 5). Однако ранг схемы увеличился до 7, что приводит к увеличению задержки срабатывания схемы.
1.6. Анализ комбинационных схем.
Задачи анализа КС возникают при необходимости проверить правильность синтеза (на этапе проектирования) или определить БФ, реализуемую КС (при анализе или ремонте схем). Все существующие методы анализа делятся на прямые и косвенные.
В результате анализа КС прямым методом получается множество наборов входных переменных, обеспечивающих заданное значение на выходе, что позволяет записать в алгебраическом виде БФ, реализуемую схемой. К прямым методам относится метод p- алгоритма.
Применение косвенныхметодов дает возможность определить реакцию схемы на заданный набор входных переменных в статике или проанализировать переходный процесс смены одного входного набора на другой. Примерами косвенных методов анализа, являются методы синхронного и асинхронного моделирования.
Все упомянутые методы анализа являются машинoориентированными, что позволяет выполнить анализ схемы на ЭВМ.
Для всех методов анализа необходимо описать схему в виде схемного списка, в который включается в общем случае следующие данные: номер ЛЭ в схеме; логическая функция, реализуемая ЛЭ; входные переменные для данного ЛЭ. Например, схема представленная на рис.9, может быть описана следующим списком:
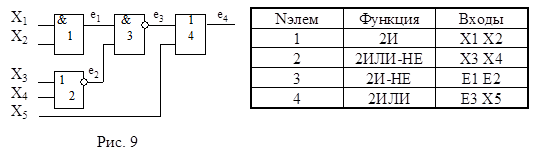
|
Дата добавления: 2020-06-09; просмотров: 769;











