Канонический метод синтеза комбинационных схем.
Как отмечалось выше, комбинационная схема (КС) может иметь несколько выходов. При каноническом методе предполагается, что каждая выходная функция реализуется своей схемой, совокупность которых и даёт требуемую КС. Поэтому синтез сложной КС с n выходами заменяется синтезом n схем с одним выходом.
Согласно каноническому методу синтез КС включает в себя ряд этапов.
1. Подлежащая реализации булева функция (или её отрицание) представляется в виде СДНФ.
2. С использованием методов минимизации определяется минимальная ДНФ (МДНФ) или минимальная КНФ (МКНФ). Из полученных двух минимальных форм выбирается более простая.
3. Булеву функцию в минимальной форме согласно п.2 представляют в заданном (или выбранном разработчиком) базисе .
4. По представлению функции в заданном базисе строят комбинационную схему.
Необходимо отметить, что подлежащая реализации булева функция F(X1,X2,...,Xm) может быть задана не на всех возможных наборах аргументов X1, X2, ..., Xm. На тех наборах, где функция неопределенна, её доопределяют так, чтобы в результате минимизации получить более простую МДНФ или МКНФ. При этом упростится и сама КС. Кроме того, довольно часто с целью получения ещё более простого представления функции МДНФ, полученная в п.2, представляется в так называемой скобочной форме, т.е. выносятся за скобки общие части импликант МДНФ.
Рассмотрим канонический метод синтеза на примере построения схемы полного одноразрядного двоичного сумматора.
Как известно из курса машинной арифметики, полный одноразрядный сумматор - это устройство, которое осуществляет сложение по mod 2 соответствующих разрядов (X1,X2) двоичных чисел с учётом переноса (Рm) в данный разряд из соседнего младшего разряда суммы. Сумматор вырабатывает цифру результата (S) в данном разряде и перенос (Рс) в соседний старший разряд суммы. Таблица истинности такого сумматора (т.е. представление булевой функции, которую он реализует, в виде СДНФ) представлена ниже.
| X1 | ||||||||||
| X2 | ||||||||||
| ||||||||||
| S | ||||||||||
| Pc |
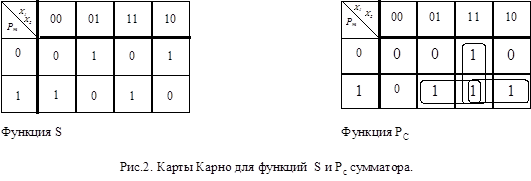
|
Необходимо получить булевы функции S=F1(X1,X2,Рm) и Рс=F2(X1,X2,Рm). Карты Карно для этих функций приведены ниже (рис.2).
Как следует из приведённых карт, МДНФ соответствующих функций имеет вид:
|
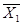
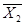 Pm+
Pm+ 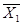 X2
X2 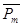 +X1
+X1 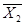
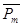 + X1 X2 Pm
+ X1 X2 Pm
Pc= X1 X2+X1 Pm+X2 Pm
Полученная система булевых функций представлена в базисе И, ИЛИ, НЕ. Соответствующая ей КС приведена на рисунке 4.
Полученную комбинационную схему можно упростить, вынеся за скобки общие части в выражениях для S и Рc, однако существенного результата это не даст (желательно самостоятельно в этом убедиться).
Значительно упростить схему можно, если воспользоваться другим базисом, например логическим элементом "ИСКЛЮЧАЮЩЕЕ ИЛИ". В этом случае выражение для S можно записать S = (X1+X2+ Рm)mod2= X1Å X2Å Рm. Тогда схема для S будет иметь вид (рис.3).
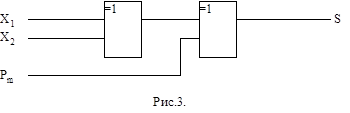
|
Иногда для синтеза КС с несколькими выходами может использоваться следующий приём. Будем считать, что при синтезе схемы сумматора функция S является функцией четырёх переменных: S=f(X1,X2,Рm,Рс). Таблица истинности для этого случая принимает вид изображенный в таблице 2.
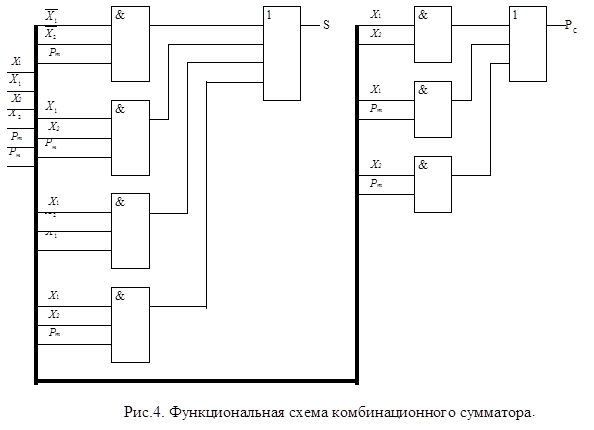
|
| X1 | ||||||||||||||||
| X2 | ||||||||||||||||
| Pm | ||||||||||||||||
| Pc | ||||||||||||||||
| S | X | X | X | X | X | X | X | X |
|
Неопределённые значения для S соответствуют наборам, которые никогда не могут быть в реальной схеме. Карта Карно для функции S=f(X1,X2,Pm,Pc) представлена на рис.5.
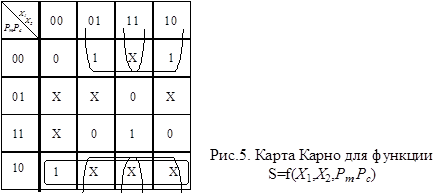
|
В результате минимизации, получается :
|
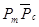 +X2
+X2 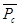 +X1
+X1 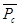 + X1 X2 Pm = (Pm+X2+X1)
+ X1 X2 Pm = (Pm+X2+X1) 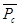 + X1 X2 Pm
+ X1 X2 Pm
Сравнивая выражения (2) и (3), отмечаем, что функция S=f(X1,X2,Pm,Pc) проще, чем функция S=f1(X1,X2,Pm). Схему, соответствующую (3), предлагается построить самостоятельно.
Т.о. задача синтеза имеет обычно несколько решений. Для сравнения различных вариантов комбинационных схем используют их основные характеристики: сложность и быстродействие.
Дата добавления: 2020-06-09; просмотров: 624;











