Все (некоторые) S есть (не есть) P

При выполнении логических операций удобно использовать круговые схемы Эйлера. Графическое изображение соотношений между понятиями по объему одинаково для одних и тех же видов суждений, но у большинства из них допускается более одного варианта. Желательно их знать и хорошо помнить.

Общеутвердительное суждение. Всем предметам приписывается какое-то свойство. Оно, следовательно, является общим по количеству и утвердительным по качеству. Структура такого суждения - "Все S есть P". Например, 1) "Все планеты - небесные тела" или 2) “Квадрат - прямоугольник с равными сторонами”; а так как единичные суждения тоже относятся к общим, то и высказывания 3) "Уральские горы протянулись с севера на юг" и 4) “Данное преступление совершено вчера” тоже относятся к общеутвердительным суждениям. Их принято обозначать буквой A (a) - первой гласной латинского affirmo (утверждаю). Тогда ту же структуру можно изобразить так: S a P; читается: все S есть P.

Если изобразить соотношение понятий, входящих в это суждение, круговыми схемами, то общеутвердительному суждению, как правило, соответствует нижняя часть рисунка 4. В нем все S входят в объем понятия P (отношение подчинения).

Так, все планеты, естественно, должны входить в круг тел, относимых нами к небесным телам, Уральские горы, согласно суждению (3), входят в число всего того, что можно отнести к протянувшемуся с севера на юг, а преступление, о котором речь в суждении (4), обязательно должно охватываться кругом событий, произошедших вчера. И только для суждения (2) надо брать верхнюю часть этого рисунка, так как данные понятия равнозначны и потому изображающие их круги сливаются.

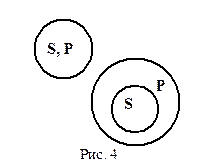
Рис. 4

Следует помнить, что кругами надо изображать то, что сказано в суждении, а не то, что есть в действительности. Расхождение между тем и другим возникает в случае ложных высказываний. Например, суждению “Птица - летающее позвоночное” соответствует нижняя часть рисунка 4, хотя не все птицы входят в число летающих позвоночных. Но это говорит только о том, что данное суждение (относящее всех птиц к летающим животным) ложно.

Общеотрицательное суждение. Этот вид суждения является общим по количеству и отрицательным по качеству - у всех предметов отрицается какое-либо свойство: все (никакое) S не есть P. 1) "Никакая параллель не пересекает экватор", 2) "Дельфин не рыба", 3) “Всякая война не обходится без жертв” - примеры таких суждений. Их обозначают первой гласной из латинского nego (отрицаю) - E (e). Краткая запись: S e P. Читается: все (никакое) S не есть P.

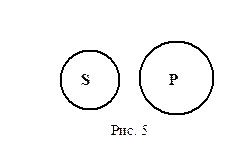
Рис. 5

Общеотрицательное суждение "Ни одно S не есть P" изображается двумя кругами вне друг друга, как для несравнимых понятий (рис. 5).

Частноутвердительное суждение образуется тогда, когда берется высказывание, частное по количеству и утвердительное по качеству, стало быть, части предметов приписывается какое-то свойство. Например, 1) "Некоторые студенты изучают китайский язык", 2) "Большинство учебников не являются задачниками”, 3) “Преступники порой избегают наказания”. Символическим обозначением ему служит вторая гласная из того же слова affirmo - I (i), так что записывается оно так: S i P; читается: некоторые S есть P.

Частноутвердительным суждениям соответствуют две круговые схемы (рис. 6). Чаще всего S и P являются перекрещивающимися понятиями поэтому круги, отображающие объемы субъекта и предиката пересекаются. Так, круг лиц, называемых студентами, лишь частично накладывется на круг лиц, которые изучают китайский язык; и в первой и второй категории людей есть такие, кто принадлежит только к одной из них и не прирадлежит к другой. Учебники же и задачники находятся в отношении подчинения (хотя лишь некоторые учебники - задачники, но все задачники являются учебниками, поэтому круг для P полностью входит в круг для S).

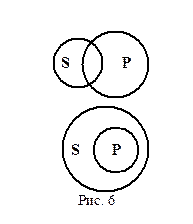
Рис. 6

Используя круговые схемы, надо помнить, что, строго говоря, содержание понятий задается только определением, а оно чаще всего лишь подразумевается и иногда может быть истолковано неодинаково. Так, в суждении о преступниках под избегающими наказания можно иметь в виду вообще всех, кто сумел уйти от него: нерадивых работников, прошрафившихся учеников и т.п. Тогда между S и P отношение перекрещивания. Но если сюда отоносить только преступников, которым удалось избегнуть кары, то тогда те же понятия окажутся в отношении подчинения.

Частноотрицательное суждение, как легко понять по аналогии с предыдущими, является частным по количеству и отрицательным по качеству. Для обозначения берется вторая гласная из слова nego - O (o). Тогда структура суждения - S o P; читается: некоторые S не есть P. 1) "Некоторые законы не имеют обратной силы", 2) “Большинство музыкантов не скрипачи”, 3) “Иные из бабочек не являются однодневками”, 4) “По меньшей мере часть грибов не относят к высшим растениям”.

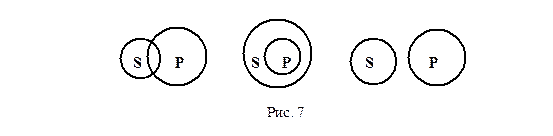
Рис. 7

Соотношение по объему может изображаться тремя вариантами, показанными на рисунке 7. Закон, с одной стороны, и все то, что можно назвать имеющим обратную силу, с другой стороны (о которых идет речь в первом суждении), образуют, очевидно, отношение пересечения. Легко также понять, что в суждении (2) понятия “музыкант” и “скрипач” образуют отношение подчинения. В суждении (3), однако, такой однозначности уже нет. Если под “однодневками” иметь в виду только однодневных бабочек, то тогда между понятиями, стоящими на месте субъекта и предиката, отношение подчинения. Но, строго говоря, под "однодневным” можно понимать и все, что длится не более одного дня, - от грозы до курса ценных бумаг; в таком случае те же понятия образуют отношение пересечения. В суждении (4) речь идет о несовместимых понятиях, поскольку все грибы - низшие растения (поэтому не только некоторые из них, но и все они не относятся к высшим). Тем не менее данное суждение является истинным, так как в нем дается осторожное ручательство всего лишь за часть грибов. Напомним еще раз, что в традиционной логике квантор “некоторые” имеет (когда не сделано специальных оговорок) именно такой смысл - “некоторые, но, может быть, и все”.

Следует твердо помнить, что, определяя вид суждения по объединенной классификации, мы должны принимать во внимание только то, что в нем говорится, а не отображаемую в нем действительность. Между ними может не быть совпадения, поскольку встречаются высказывания также и ложные. Например, суждение “Утка - домашняя птица” является, очевидно, общеутвердительным и ему соответствует круговая схема рис. 4 (все утки входят в круг домашних птиц). В действительности же их следовало бы изображать, как легко понять, пересекающимися, ведь некоторые из уток являются дикими и, следовательно, не входят в число домашних птиц. Тем не менее в дальнейшем анализе данное суждение все равно должно остаться для нас общеутвердительным по своим логическим свойствам и его надо будет изображать кругами для подчиненных понятий, но только при этом придется помнить, что мысль, содержащаяся в этом суждении, является ложной.

Логический квадрат

Благодаря количественным и качественным характеристикам даже суждения с одними и теми же субъектами и предикатами могут различаться между собой. Их называют суждениями с одинаковой материей, потому что в них речь идет об одних и тех же предметах и об одних и тех же их свойствах, только в утвердительных суждениях эти свойства приписываются, а в отрицательных - отрицаются, в частных говорится о некоторых из предметов, в то время как в общих речь идет обо всех. Между суждениями этого рода устанавливаются определенные твердые соотношения по их истинностным значениям. Так, если мы возьмем общеотрицательное суждение "Ни один из киосков в этом квартале не торгует цветами" и если оно истинно, то тогда ни в коем случае не может быть истинным частноутвердительное суждение о том же - "Некоторые из киосков в этом квартале торгуют цветами". Точно так же, если бы второе было истинным, то в таком случае обязательно ложным было бы первое. Отношения между другими парами суждений с тем же субъектом и таким же предикатом выглядят иначе, но главное, что они существуют и их можно выявить.

Всю систему взаимообусловленности истинностных значений суждений с одинаковой материей удобно изобразить графически с помощью так называемого логического квадрата[Для надлежащего освоения этого трудного параграфа желательно сначала выполнить упражнения 1-3 в конце раздела, затем 4-12 (в процессе изучения параграфа), потом все остальные задачи и упражнения.].

Буквы на его углах символизируют различные виды суждений - A, E, I, O (см. рисунок 8). А его стороны и диагонали выражают всю совокупность возможных отношений между ними. Линия AE образует отношение противоположности или, иначе, контрарности. Пары этих суждений никогда не могут быть одновременно истинными; в нашем примере истинность того и другого означала бы, что верно как утверждение о том, что все киоски в этом квартале торгуют цветами, так и о том, что ни один из них ими не торгует. Очевидно, такое невозможно. Другие же сочетания значений для пары A и E допустимы: могут быть оба ложны и может одно быть истинным, а другое ложным. Отсюда получается правило: когда одно из противоположных суждений (A или E) истинно, то можно уверенно делать вывод, что противоположное ему истинным не является, когда же одно ложно, то никаких выводов о противоположном делать нельзя, оно может быть и тем, и другим.

Две расположенные по диагонали пары AO и EI составляют отношение противоречия или контрадикторности. Правило для них легче всего запомнить, потому что их истинностные значения регулируются законом исключенного третьего: когда одно истинно, другое обязательно ложно и наоборот. Это значит, установив истинностное значение одного из членов пары, каким бы оно ни было, мы тем самым однозначно установили значение лежащего против него по диагонали.

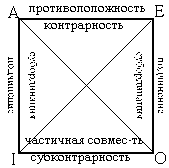
Рис. 8

Нижняя сторона квадрата выражает отношениечастичной совместимости,или, иначе, субконтрарности. В отличие от противоположных суждений эта пара никогда не бывает одновременно ложной. В принципе можно рассматривать данное обстоятельство как следствие, обусловленное первыми двумя отношениями. В самом деле, попробуем воспользоваться теми соображениями, которые были высказаны о противоположных и противоречащих суждениях, предположив сначала, что I ложно, и определив значение O в таком случае, затем проделаем то же самое, отправляясь от того, что ложно O. Итак, допустим, что I ложно. Тогда противоречащее ему суждение E истинно (ибо лежащие по диагонали пары не могут быть вместе ни истинными, ни ложными); отсюда следует, что противоположное E суждение A должно быть ложным (так как из противоположных пар суждений истинным может быть только одно); но, установив ложность A, мы обязаны признать истинным противоречащее ему суждение O. Совершенно аналогично, допустив ложность O, мы обратным порядком придем к утверждению, что I в таком случае должно быть истинно. Однако при других истинностных значениях их взаимообусловленность отсутствует. Предположив, что I (O) истинно, мы сможем, правда, прийти к выводу о ложности противоречащего ему суждения E (A), но дальше рассуждение оборвется, так как при ложности одного из противоположных понятий другое может иметь любое из двух возможных значений, а значит и лежащее против него по диагонали противоречащее (и одновременно субконтрарное относительно I) суждение O может быть как истинным, так и ложным. Таким образом, получается правило в отношении субконтрарных суждений: когда одно из них ложно, другое обязательно истинно, но когда одно из них истинно, то о другом ничего сказать нельзя.

Стороны квадрата AI и EO выражают отношение подчиненияили субординации. В какой-то мере его можно было бы уподобить отношению части и целого: истинность общего суждения (и утвердительного A, и отрицательного E) означает одновременно истинность частного (I и соответственно O). Если мы знаем, что все металлы электропроводны, то тем более верно говорить это о некоторых из них. Однако когда общее суждение ложно, то о частном сказать ничего нельзя; к примеру, отрицание того, что все представители данной философской школы - идеалисты, может означать как то, что их там только часть, так и то, что их там вообще нет. При движении же от частного к общему все обстоит наоборот. Лишь когда частные суждения ложны, можно делать вывод о том, что подчиняющее его суждение тоже ложно (если неверно, что часть предметов обладает (не обладает) каким-то свойством, то тогда тем более неверно сказать то же самое про все). Но если частное суждение истинно, то это оставляет нас в неведении относительно истинности или ложности общего суждения. Мы можем, например, узнать, что некоторые медведи в данной географической зоне бурые; это обстоятельство, однако, не позволит нам узнать, есть ли там еще и другие медведи или они все там бурые. Итак, основываясь на выводах об истинности общего суждения A и E, можно прийти к заключению об истинности подчиненных им суждений I и соответственно O, а от ложности частного суждения I и O можно прийти к утверждению о ложности соответствующих подчиняющих суждений A и E. При ложности же общих и истинности частных суждений никакие выводы по линии подчинения невозможны.

И это правило тоже можно получить в качестве следствия из отношений противоречия и противоположности. Так, если общее суждение A (E) истинно, то тогда обязательно ложно противоположное ему суждение E (A), а отсюда по линии противоречия получим, что истинно подчиненное по отношению к A (E) суждение I (O). И таким же путем, предположив ложность частных суждений, мы придем к выводу о ложности подчиняющих их общих. При других исходных значениях рассуждения не получатся из-за того, что при ложности общих суждений не допускаются выводы по линии противоположности.

Необходимо помнить о том, что теория логического квадрата построена только для неопределенно-частных суждений, когда под словом "некоторые" подразумевается "как минимум некоторые, а может быть и все". На определенно-частные, или выделяющие суждения с квантором "только некоторые" она не распространяется. Система отношений истинностных значений для этого случая не укладывается в квадрат, но зато она выглядит проще. 1) Когда истинно одно из общих суждений, то все остальные обязательно ложны; обратное тоже верно. 2) Частные суждения либо оба вместе истинны, либо оба вместе ложны. 3) Когда частные суждения истинны, то оба общих обязательно ложны.

Законы логического квадрата, как и остальные логические законы, не зависят от содержания высказываний. О чем бы ни шла речь, все отмеченные правила действуют неукоснительно. Даже если нам непонятно содержание, то все равно, опираясь на одну только логическую форму, можно сделать правильные выводы или проверить, верно или нет построено то или иное рассуждение с использованием суждений одинаковой материи.

Допустим, перед нами такой текст: "Неправильно говорить, что (1) некоторые целлы представляют собой наосы, и еще более ошибочно считать, будто (2) никакие целлы не являются наосами". Чтобы разобраться с содержанием этих мало кому известных понятий, надо сначала решить, в каком из двух смыслов употребляется слово "некоторые". Неопределенно-частным оно быть не может, поскольку с таким квантором противоречащие друг другу суждения (1) и (2) не могли бы быть одновременно ложными. Получается, "некоторые" означает "только некоторые", и перед нами определенно-частное суждение (1) "Только некоторые целлы есть наосы", которое объявляется ложным вместе с общеотрицательным суждением (2). Из истинностных соотношений для суждений с таким квантором следует, что частные суждения бывают ложными лишь одновременно. Тогда значит и суждение частноотрицательное тоже надо признать ложным. Истинным остается только общеутвердительное суждение A: "Все целлы - наосы" (то и другое представляет собой название главного помещения в древнегреческом храме).

Овладение правилами логического квадрата требует обязательной проработки всех относящихся к нему упражнений и задач. Его простые по-отдельности истинностные соотношения в своей совокупности образуют довольно громоздкую и сложную систему.