Методы описания цифровых автоматов
Чтобы задать цифровой автомат S, необходимо описать все элементы множества S = { A, X ,Y, d, l, a1}, то есть входной и выходной алфавиты и алфавит состояний, а также функции переходов и выходов. Из множества способов описания обычно используются практически равноценные табличный и графический (с помощью ориентированных графов) [4].
Пример общего описания автоматов Мили таблицами переходов и выходов дан в таблице 14 и таблице 15.
Таблица 14 Таблица15
Общий вид таблицы переходовОбщий вид таблицы выходов
автомата Милиавтомата Мили
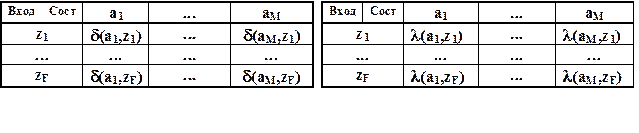 Строки этих таблиц соответствуют входным сигналам множества X, а столбцы - состояниям A, причём крайний левый столбец обозначен как начальное состояние инициального цифрового автомата a1.
Строки этих таблиц соответствуют входным сигналам множества X, а столбцы - состояниям A, причём крайний левый столбец обозначен как начальное состояние инициального цифрового автомата a1.
На пересечении столбца am и строки zf в таблице переходов ставится состояние as=d(am, zf), в которое автомат переходит из состояния am под действием сигнала zf. В таблице выходов - соответствующий этому переходу выходной сигнал wg=l(am, zf).
Пример табличного описания полностью определённого цифрового автомата Мили S1 с тремя состояниями, двумя входными и двумя выходными сигналами приведён в таблице 16 и таблице 17.
Таблица 16 Таблица 17
Таблица переходов а. Мили S1 Таблица выходов а. Мили S1
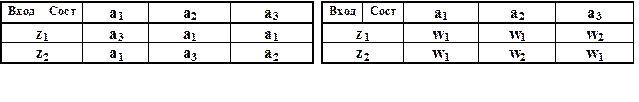
Заголовочная строка и столбец обозначены одинаково для обеих таблиц, поэтому для экономии времени можно производить описание автомата Мили одной совмещённой таблицей переходов и выходов, например, таблицей 18.
Таблица 18
Совмещённая таблица переходов и выходов автомата Мили S1
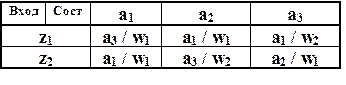
Для частичных автоматов, у которых функции d и l определёны не для всех пар (am, zf) Í A´X , на месте неопределённых состояний и неопределённых выходных сигналов ставится какой либо специальный символ, например, прочерк. Пример табличного описания частичного автомата приведён в совмещённой таблице 19.
Таблица 19
Совмещённая таблица для частичного а. Мили S2
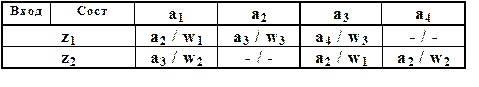
Так как в автомате Мура выходной сигнал зависит только от состояния, то автомат Мура описывается одной - отмеченной - таблицей переходов (общая форма - таблица 20, пример - таблица 21), в которой каждому её столбцу приписан, кроме состояния am, ещё и соответствующий выходной сигнал wg=l(am).
Таблица 20
Общий вид отмеченной таблицы переходов автомата Мура
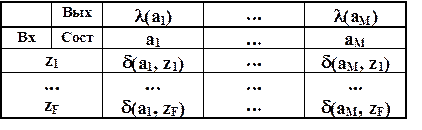
Таблица 21
Отмеченная таблица переходов автомата Мура S3
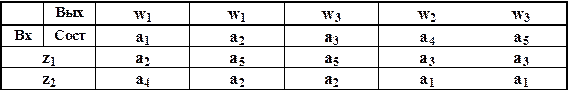
Граф автомата - ориентированный связный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними.
Две вершины графа автомата am и as (исходное состояние и состояние перехода) соединяются дугой, направленной от am к as , если в автомате имеется переход из am в as , то есть если as = d(am, zf) при некотором zf ÎX. Дуге (am, as) графа автомата приписывается входной сигнал zf и выходной сигнал wg = l(am, zf), если он определён, и ставится прочерк в противном случае. Если переход автомата из состояния am в состояние as происходит под действием нескольких входных сигналов, то дуге (am, as) приписываются все эти входные и соответствующие выходные сигналы.
При описании автомата Мура в виде графа выходной сигнал wg = l(am) записывается внутри вершины am или рядом с ней.
На рис.22, рис.23 и рис.24 приведены графы цифровых автоматов S1, S2 и S3, описанные ранее в таблице 18, таблице 19 и таблице 21
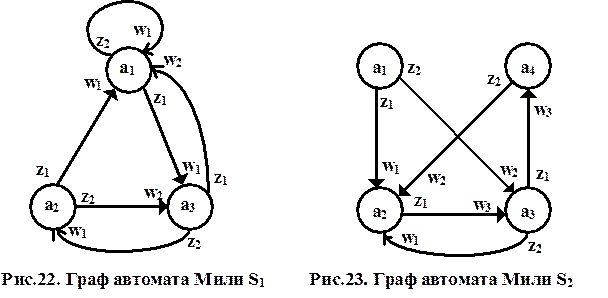

В технических целях используются только детерминированные цифровые автоматы, в которых выполнено условие однозначности переходов: - автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более, чем в одно состояние. Применительно к табличному способу задания описания автоматов это означает, что в клетках переходов/выходов указывается только по одному состоянию/выходному сигналу. Применительно к графическому способу задания описания автоматов это означает, что в графе автомата из любой вершины не могут выходить две или более дуги, отмеченные одним и тем же входным сигналом.
Дата добавления: 2020-06-09; просмотров: 631;











