И различным расстоянием повернутой секции
дозвуковой части от минимального сечения 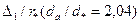
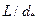
| А при 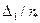
| ||
| 0,32 | 0,45 | ||
2,82
4,07
4,78
0 
| 0,034 0,159 0,049 -0,12 | 0,018 0,028 - - | 0,008 0,014 - - |
_________________
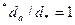 .
.
Наличие асимметричных возмущений при перерасширенном течении в сверхзвуковой части сопла приводит к несимметричному отрыву потока от стенки и к существенному изменению поперечной силы.
Эксцентриситет реактивной силы вследствие нарушений симметрии выходного среза рассчитывают по результирующей сил давления на неуравновешенную часть сопла. В случае косого среза, плоскость которого наклонена под малым углом 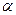 к плоскости поперечного сечения, приближенно имеем (рн=0)
к плоскости поперечного сечения, приближенно имеем (рн=0)
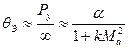 .
.
Наиболее универсальным подходом является решение задачи пространственного течения рабочего тела в сопле и интегрирование по контуру рассчитанного распределения давления по стенке.
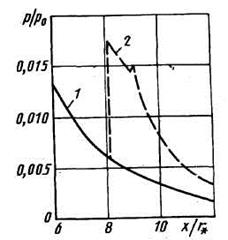
Для исследования безотрывных сверхзвуковых пространственных течений газа в соплах применяются различные численные методы (метод малых возмущений, послойный метод характеристик, метод сквозного счета, разностный метод второго порядка точности, стационарный аналог схемы С.К. Годунова), а также экспериментальные методы (например, с использованием дифференциальной установки). Для случая поворота оси конического сопла (в сечении, соответствующем у 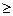 1,1) все методы дают одинаковые результаты (рис. 4.7,
1,1) все методы дают одинаковые результаты (рис. 4.7, 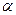 =6°) [23].
=6°) [23].
Относительная поперечная сила в направлении, параллельном плоскости выходного среза сопла( 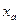 =12),в начальном сечении поворотного колена (х=0,63) равна Ру=sin
=12),в начальном сечении поворотного колена (х=0,63) равна Ру=sin 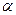 =0,104, а в его выходном сечении, одновременно являющемся начальным сечением осесимметричного раструба (0,65
=0,104, а в его выходном сечении, одновременно являющемся начальным сечением осесимметричного раструба (0,65 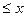 <12),
<12),
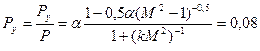 .
.
В выходном сечения сопла (ха=12) Ру=-0,007. Такое же искажение потока возникает и при работе поворотной секции сопла. Коэффициент усиления поворотной секции сопла Ку=Ру/(Р 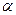 )=0,8…1,2; причем большие значения Ку соответствуют меньшим расстояниям между сечениями критическим и разъема (1,1
)=0,8…1,2; причем большие значения Ку соответствуют меньшим расстояниям между сечениями критическим и разъема (1,1 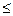 у
у 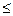 2; у
2; у 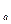 =4,5;
=4,5; 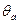 =10°). Шарнирный момент в этом случае возрастает с ростом у:М
=10°). Шарнирный момент в этом случае возрастает с ростом у:М 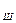 =М
=М 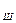 /(Ро
/(Ро 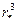 )=1,2; 2,3; 3 при у=1,1; 1,2; 1,4 соответственно. Если в месте разъема имеются уступы, то необходимо учитывать возможность образования отрывных зон.
)=1,2; 2,3; 3 при у=1,1; 1,2; 1,4 соответственно. Если в месте разъема имеются уступы, то необходимо учитывать возможность образования отрывных зон.
При несимметричном выходном срезе сопла распределение давления на боковых стенках не изменяется, если линии Маха, отходящие от выходных кромок, попадают на свободные границы истекающей струи.
Даже если угол Маха немного больше, чем угол косого среза, то осесимметричная модель по-прежнему является достаточно точной.
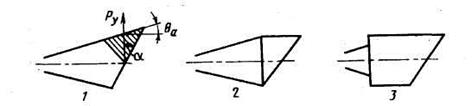
Если воспользоваться моделью одномерного течения в сопле с косым срезом (рис. 4.8), то для относительной боковой силы в пустоте получим
В случае рн>0 боковая сила зависит от разности р-рн, и могут понадобиться более точные методы расчета распределения давления на неуравновешенную часть сопла.
К осесимметричной части сопла может быть пристыкован кососрезанный насадок, угол наклона контура которого меньше угла наклона осесимметричной части (см. поз. 2 на рис. 4.8) . Тогда в месте стыковки возникает косой скачок, давление существенно возрастет, что приведет к увеличению Ру. При известном донном давлении рд в ступенчатом сопле (см. поз. 3 на рис. 4.8) распределение давления в цилиндрическом насадке рассчитывается, например, с помощью стационарного аналога метода С.К. Годунова. Возникающая при этом поперечная сила принимает наибольшее значение, если присоединение границ струи, истекающей из узкой части, происходит в области неуравновешенной части кососрезанного насадка. Максимальное давление в области присоединения в 1,9 и более раз превышает донное давление и зависит от числа Маха на границе струи:

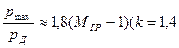 ;
; 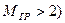 .
.
|
|
|
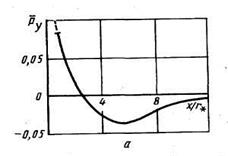
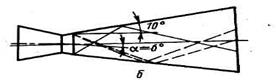
Рис. 4.7. Распределение поперечной силы (а) в коническом сопле с поворотом оси (б)
|
Рис, 4.8 Распределение давления на стенке различных сопел с косым срезом:
1 - коническое сопло; 2 - коническое с цилиндрической приставкой; 3 –коническо-цилиндрическое.
Дата добавления: 2016-06-29; просмотров: 1967;











