Перемешивание жидких и сыпучих смесей

Перемешивание широко применяется в пищевой промышленности для образования эмульсий и суспензий, однородных смесей сыпучих материалов и других сплошных сред, а также для интенсификации процессов тепло- и массообмена. Перемешивание заключается в измельчении элементов жидких, твердых или сыпучих сред и их равномерном перераспределении в пространстве с целью выравнивания состава смеси во все более и более малых объемах.

Из процессов перемешивания в самостоятельную группу выделены процессы гомогенизации.

Полнота и завершенность процесса перемешивания (или, в других терминах, эффективность перемешивания, достигнутая однородность смеси и др.) может оцениваться величиной (β называемой коэффициентом неоднородности смеси:

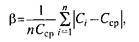
где С С_ср — концентрация рассматриваемого ингредиента в смеси: текущая (в точке i) и средняя (ее математическое ожидание); n —число точек измерения текущей концентрации; i= 1, 2,...,n

Перемешивание идеально, если max β = 0.

Соответственно характеристику однородности смеси логично выразить величиной R = 1 — β

Введенную характеристику неоднородности в смеси β можно назвать относительным средним отклонением концентрации рассматриваемого ингредиента смеси от среднего ее значения или от математического ожидания концентрации.

В выражении для коэффициента неоднородности смеси используют концентрации одного из ингредиентов, которые можно измерить только в некотором объеме. Такой объем мы называем мерным, а его характерные размеры — масштабом оценки неравномерности состава смеси. В зависимости от масштаба оценки в мерный объем может попадать разное количество ингредиентов и соответственно может меняться результат оценки. В общем случае результат оценки зависит также от ориентации мерного объема в пространстве. Изменяя его ориентацию, можно найти такую, при которой неравномерность состава смеси в целом будет максимальной.

В практических измерениях неоднородности смеси поступают следующим образом. В ряде точек ί перемешиваемого объема по заранее намеченной схеме одновременно отбирают пробы концентрации рассматриваемого компонента Сί и вычисляют среднюю величину называемую математическим ожиданием, и коэффициент неоднородности смеси β по приведенной выше формуле. При необходимости находят максимальное ее значение.

Обратим внимание на важнейшую роль масштаба оценки в измерении неоднородности смеси и проиллюстрируем это следующим примером.

Пусть в кубическом объеме, равном 1 м³, с ребром куба, равным 1 м, находится 0,5 м3 одного и столько же второго сыпучего материала с равными насыпными плотностями. Пусть материалы не перемешаны между собой и занимают объемы параллелепипедов с ребрами 1 х 1 х 0,5 м, как это показано на рисунке 16.1, а в проекции на плоскость чертежа.

Если, оценивая неоднородность смеси этих материалов, в качестве мерного объема взять исходный куб с ребром 1 м, то в соответствии с выражением для коэффициента неоднородности смеси β максимальное его значение получим равным β= 0. Это определяется тем, что массоваяконцентрация (в долях единицы), вычисляемая для определенности по первому продукту,

Если уменьшить размеры мерного объема, взяв в качестве него объем параллелепипеда с размерами в плане 1 х 0,5м, то максимальное значение оценки неоднородности смеси получим при условии, что вначале весь первый, а потом весь второй материал разместим в мерном объеме. Тогда для двух измерений с индексами 1 и 2 получим

С_ср = 0,5; С₁ = 1; С₂ = 0; max β = 1.

Иными словами, перемешивание при таком мерном объеме предельно плохое (отсутствует вовсе). Оценка не изменится, если продолжать уменьшать мерный объем.

Характерный размер мерного объема m в данном случае должен быть принят равным 0,5 м, т. е. равным минимальному размеру мерного параллелепипеда.

Изобразив на рисунке 16.1, б, значения max β в зависимости от характерного размера мерного объема m, получим, что при переходе через граничное значение характерного размера мерного объема (масштаба оценок m), равное 0,5 м, происходит скачкообразное изменение результата оценок.

Если в этом же примере объемы, занимаемые каждым материалом, уменьшить в два раза и половину из них переместить в пространстве на предельно возможную величину, равную 0,5 м, как это показано на рисунке 16.1 в, оценка неоднородности смеси изменяется. Это показано на рисунке 16.1, г. Граничное значение характерного размера масштаба оценок сместится к 0,25 м.

Зависимости на рисунке 16.1 носят скачкообразный (разрывной) характер. Это связано с использованием в оценках максималь­ного значения коэффициента неравномерности перемешивания. Если принять равновероятное по всем направлениям ориентирование мерного объема, эти зависимости преобразуются в средневзвешенные, изображенные на рисунке 16.1 жирными линиями.

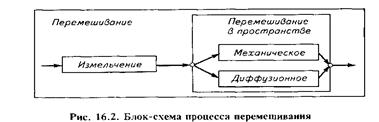
Блок-схема процесса перемешивания (рис. 16.2) может быть представлена состоящей из двух последовательно протекающих процессов: измельчения и перемещения в пространстве.

В общем случае возможны два механизма перемещения частиц в пространстве:

в результате механического перемещения рабочими органами смесителя;

вследствие диффузионного перемещения силами молекулярного взаимодействия в эмульсиях, суспензиях и золях.

В сыпучих смесях диффузионного перемещения ингредиентов не наблюдается.

Механическое перемещение раздробленных частиц происходит одновременно с измельчением, когда частицы разрушаются при попадании между подвижным смесительным органом (ножом) и неподвижной декой. При этом одна из разрушенных частиц увлекается подвижным органом и переносится в пространстве на некоторое расстояние. Это расстояние случайным образом изменяется в зависимости от ориентации разрушаемой частицы. Однако даже если в результате механического перемещения частиц не достигнуто идеального их распределения в пространстве, в эмульсиях, суспензиях и золях оно будет достигнуто через некоторое время за счет диффузии. Твердые и жидкие частицы дисперсной фазы в этих системах диффундируют, подчиняясь феноменологическому закону Фика.

В связи с отсутствием диффузионного перемещения твердых сыпучих частиц дисперсной фазы, распределенных в твердой же дисперсионной среде, их перемещение в пространстве определяется только механическим переносом. Механический перенос может сопровождаться или не сопровождаться измельчением частиц или конгломератов частиц системы.

Как во всяких последовательно протекающих процессах, суммарная скорость сложного процесса определяется скоростью самого медленного из них. Остальные процессы протекают как бы квазистационарно. В процессе перемешивания на разных его стадиях то один, то другой из составляющих процессов может опережать другой по массовой скорости. Обычно в начале перемешивания измельчение частиц дисперсной фазы определяет скорость суммарного процесса, а в конце — наоборот. Поэтому точный вывод расчетных зависимостей для массовой скорости перемешивания затруднителен. Задача облегчается тем, что оба процесса, составляющих сложный процесс перемешивания, описываются функционально одинаковыми зависимостями.