Потребления электрической энергии

Мощность, потребляемая источником,

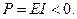
(ЭДС Е и ток I имеют разные знаки).

Мощность потерь на внутреннем сопротивлении источника

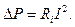
Мощность, потребляемая из сети,

Баланс мощностей

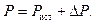
Полезной мощностью во втором режиме работы является мощность, потребляемая источником, а затрачиваемой – мощность, потребляемая из сети. Поэтому КПД равен

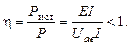
Схемы рис. 53, 54 и энергетические соотношения, приведенные выше, хорошо иллюстрируют обратимость электрических машин постоянного тока и режимы разрядки – зарядки аккумуляторных батарей. Электрическая машина может работать в режиме генератора, отдавая энергию во внешнюю цепь, или в режиме электродвигателя, потребляя энергию из сети. Аккумуляторная батарея в режиме разрядки отдает электрическую энергию во внешнюю цепь, а в режиме зарядки потребляет ее из сети.

Из схем рис. 53, 54 и соотношений, приведенных в настоящем параграфе, следует, что приемник электрической энергии может быть как пассивным элементом (или схемой, составленной из пассивных элементов), так и активным элементом – реальным источником ЭДС, работающим в режиме потребления. Любой из этих приемников или оба вместе потребляют электрическую энергию от источника-генератора.

В общем случае, если в цепи содержится q источников ЭДС, то часть из них (не более (q – 1) источников) могут работать в режиме энергопотребления, а оставшиеся (как минимум один источник) должны работать в режиме генерирования электрической энергии.

Из условия эквивалентности реальных источников напряжения и тока следует, что источник тока также может работать как в режиме генерирования электрической энергии, так и в режиме энергопотребления. Учет этих режимов работы источника тока при составлении уравнения баланса мощностей рассмотрен в следующем параграфе.

Пример 6. Рассчитать КПД источников для схемы рис. 31 (пример 3).

Решение

В схеме два источника в четвертой и шестой ветвях. КПД источника в четвертой ветви равен:

.

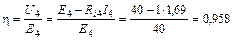Аналогичным образом определяем КПД источника в шестой ветви:

.

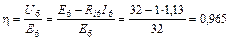Баланс мощностей

В соответствии с законом сохранения энергии в любой электрической цепи энергия, вырабатываемая всеми источниками в единицу времени, равна энергии, потребляемой приемниками электрической энергии в единицу времени. Т.е. в электрических цепях энергетический баланс можно свести к балансу мощностей.

Рассмотрим обобщенную электрическую цепь постоянного тока произвольной конфигурации, с произвольным числом источников электрической энергии и произвольным числом приемников электрической энергии. Если все источники являются источниками ЭДС, то уравнение баланса мощностей для такой цепи можно записать в виде:

.

Левая часть уравнения баланса мощностей представляет собой арифметическую сумму мощностей, обусловленных выделением тепла на сопротивлениях R при протекании через них тока I в соответствии с законом Джоуля-Ленца. Эта сумма охватывает все сопротивления R электрической цепи, в том числе и внутренние сопротивления источников R_i.

Правая часть уравнения баланса мощностей представляет собой алгебраическую сумму мощностей источников ЭДС. Выбор знака очередного члена алгебраической суммы производится в соответствии с энергетическими соотношениями, характерными для режимов генерирования и потребления электрической энергии реальным источником ЭДС, которые были рассмотрены в предыдущем параграфе. А именно: если знаки E и I одинаковы, то мощность источника EI положительна, и он работает в режиме генерирования электрической энергии; если знаки E и I различны, то мощность источника EI отрицательна, и он работает в режиме потребления электрической энергии.

При наличии в схеме источников тока их мощность также необходимо учесть в правой части уравнения баланса мощностей. Предположим, что источник тока включен между узлами a и b схемы: в узел a втекает ток I_k источника тока, а из узла b он вытекает. Тогда на выводных зажимах источника тока будет напряжение U_ab. Если знаки I_k и U_ab одинаковы, то мощность источника тока U_abI_k положительна, и он работает в режиме генерирования электрической энергии. Если знаки I_k и U_ab различны, то мощность источника тока U_abI_k отрицательна, и он работает в режиме потребления электрической энергии.

С учетом изложенного уравнение баланса мощностей для цепи, содержащей как источники ЭДС, так и источники тока, можно записать в следующем виде:

.

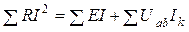Уравнения баланса мощностей удобно использовать для проверки правильности расчета токов в ветвях электрической цепи.

Пример 7. Проверить правильность расчета токов в примере 3 для схемы рис. 31 путем составления баланса мощностей.

Решение

Составляем уравнение баланса мощностей для схемы рис. 31:

R₁ I₁² + R₂ I₂² + R₃ I₃² + R₄ I₄² + R_i4 I₄² + R₅ I₅² + R₆ I₆² + R_i6 I₆² = E₄I₄ + E₆I₆.

Подставляем численные значения:

6∙2,82² + 10∙0,96² + 2∙1,86² + 7∙1,69² + 1∙1,69² + 8∙0,73² + 9∙1,13² + 1∙1,13² =

= 40∙1,69 + 32∙1,13.

Производя вычисления, получаем:

103,7 = 103,7 Вт.

Баланс мощностей сошелся. Токи рассчитаны правильно.