Параметры плазменных источников нагрева

При плазменном нагреве источник теплоты может быть представлен как двумерный круговой с нормальным законом распределения плотности теплового потока. Как правило, эти источники являются быстродвижущимися.

Вид источника показан на рисунке 7.3.

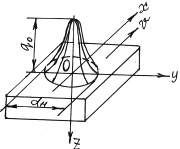
Рис. 7.3 – Схема плазменного источника нагрева.

Электрическая мощность, подводимая к плазмотрону

W = IU (Вт), (7.1)

где I – сила тока, А

U – напряжение, В.

Тепловая мощность источника

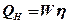, (7.2)

где η – тепловой кпд процесса (η = 0,8…0,5)

Диаметр пятна нагрева d_Н принимается равным диаметру сопла плазмотрона d_С, т.е.d_Н = d_С.

В соответствии с законом распределения плотности теплового потока (таблица 2.2) для нормального закона

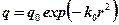, (7.3)

где q₀ – максимальная плотность теплового потока (в центре пятна нагрева О);

k₀ – коэффициент сосредоточенности кривой распределения, 1/м²;

r – расстояние рассматриваемой точки от центра пятна нагрева, м.

Коэффициент сосредоточенности зависит от диаметра пятна нагрева d_Н(м).

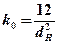(1/м²) (7.4)

Распределение температур в нагреваемом теле показано на рисунке 7.4.

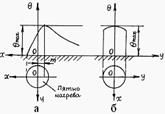
Рис. 7.4 – Распределение температур

а – в продольном сечении, б – в поперечном сечении.

При движении источника максимальная температура на пятне контакта возникает не в центре пятна (точка О), хотя в этом месте действует максимальная плотность теплового потока, а на некотором расстоянии m за ее центром в направлении, противоположном движению источника.

Если максимальная температура нагрева Θ_max выше температуры плавления Θ_пл металла, то на поверхности заготовки будет проплавление металла. Зона термического воздействия плазменного источника в поперечном сечении имеет форму сегмента (рис. 7.5).

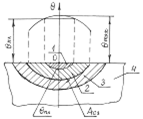
Рис. 7.5 – Зона термического воздействия плазменного источника

В слое металла, где температура нагрева превышает температуру плавления, возникает зона проплавления метала (зона 1). В слое металла, где температура превышает температуру А_С3 (зона 2) будут происходить фазовые превращения, которые можно использовать для улучшения структуры металла, уменьшения размеров зерна и др. Зона 3 – переходная к исходному металлу 4.

Для осуществления необходимого термического цикла "нагрев-охлаждение" рассчитывают соответствующий технологический режим – мощность W, скорость движения v и другие параметры.

Возможно решение и обратной задачи, когда задана максимальная температура на определенной глубине слоя металла и необходимо определить технологический режим нагрева.

В общем случае при плазменном нагреве массивных заготовок (можно принять их как полупространства) уравнение, описывающее температурное поле быстродвижущегося источника, имеет вид:

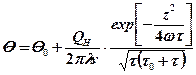, (7.5)

где Θ – температура нагрева, °С;

Θ₀ – начальная температура,°С;

Q_Н – тепловая мощность источника, Вт;

v – скорость движения источника, м/с;

λ – коэффициент теплопроводности,Вт/м⁰С;

ω – коэффициент температуропроводности, м²/с;

z – расстояние от поверхности нагрева до рассматриваемой точки, м;

τ – время, отсчитываемое от момента прохождения центра источника над рассматриваемой точкой, с;

τ₀ – постоянная времени нагрева, с, определяемая по формуле

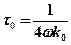
(7.6)

Рассмотрим задачу. Рассчитать максимальную температуру в массивном инструменте из быстрорежущей стали Р6М5 при нагреве плазменной струей в точке на глубине 2мм. Исходные данные: электрический режим I = 300 А; U = 60 В; тепловой кпд способа η = 0,5. Диаметр сопла плазмотрона d_c = 6 мм = 0,006 м; скорость движения источника v = 40 м/час = 0,01 м/с; теплофизические характеристики быстрорежущей стали λ = 27,2 Вт/м°С; ω = 0,057·10 ^–4 м²/с. Глубина расположения точки z = 2 мм = 0,002 м.

Принимаем инструмент как полупространство. Диаметр пятна нагрева d_Н = d_С = 0,006м.

Определяем электрическую мощность источника (формула 7.1)

W = UI = 60·300 = 18000 Вт.

Определяем тепловую мощность (формула 7.2)

Q_H = Wη = 18000·0,5 = 9000 Вт.

Определяем коэффициент сосредоточенности (формула 7.4)

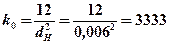1/м²;

Определяем критерий Пекле (формула 2.11)

.

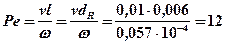Можно принять, что источник быстродвижущийся.

Принимаем начальную температуру Θ₀ =20°C.

Определяем постоянную времени при нагреве (формула 7.6)

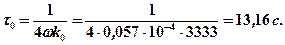
Подставляем полученные данные в формулу 7.5

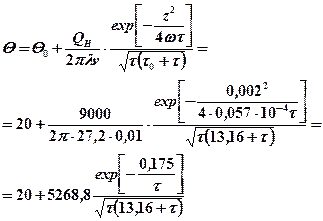
Параметр время τ входит в числитель и знаменатель. Для определения максимума температуры необходимо взять первую производную по времени и приравнять ее нулю.

Но можно решить эту задачу постепенным приближением с определенным шагом к максимуму. Для этого необходимо найти максимум правого сомножителя.

Таблица 7.1 – Расчет температуры нагрева

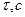
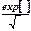
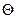
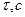
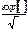
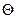
0,1	0,151		0,5	0,270
0,2	0,255		0,6	0,260
0,3	0,278		0,8	0,240
0,4	0,277		1,0	0,224

Изобразим результаты расчета графически (рис. 7.6)

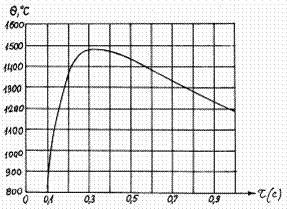
Рис. 7.6. Результаты расчета максимальной температуры.

Максимальную температуру можно принять Θ_max = 1485°С. Сечение, где находится точка с максимальной температурой, можно определить, зная скорость перемещения источника, и время, прошедшее с момента прохождения центра пятна нагрева над точкой с максимальной температурой. По графику это время τ_max ≈ 0,3 c.

Тогда m = v = 0,01·0,3 = 0,003 = 3мм. Полученное значение температуры соответствует точке на глубине z = 2 мм. Аналогично можно определить температуры и других точек по глубине тела.