Особенности использования инженерной методики расчета температур в условиях конвективного теплообмена
При решении задач теплообмена с использованием охлаждающих сред имеют место граничные условия 3-го рода. Инженерная методика расчета температур составлена для граничных условий 2-го рода. Для возможности использования инженерной методики в условиях конвективного теплообмена влияние охлаждающей среды можно представить как дополнительный сток теплоты и учесть его в структурной схеме задачи.
Рассмотрим типичную задачу конвективного теплообмена (Рис.5.2)
На полупространстве действуют одновременно круговой источник теплоты I с диаметром пятна нагрева d и круговой сток теплоты I1 в охлаждающую среду с диаметром D0. Если учесть, что распределение плотности тепловыделения источника I описывается нормальным круговым законом, то и закон распределения теплоотдачи стока I1 на поверхности пятна охлаждения также будет нормальным круговым.
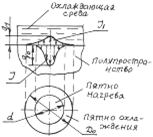
Рис. 5.2 – Влияние охлаждающей среды на температуру тела
Распределение плотности тепловых потоков в этом случае определяется специальной функцией (см. таблицу 2.2)
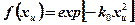 ,
,
где k0 – коэффициент сосредоточенности кривой закона распределения,
xu – координата, представляющая собой текущий радиус площадки пятна.
Расчеты показывают, что с достаточной для практики точностью коэффициент сосредоточенности k0 может быть определен по формуле
k0 = 2,8(1 – ξ), (5.15)
где 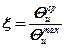 , (5.16)
, (5.16)
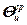 и
и 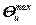 – соответственно средняя и максимальная температуры площадки диаметром d , где действует источник I, без учета охлаждающего действия среды.
– соответственно средняя и максимальная температуры площадки диаметром d , где действует источник I, без учета охлаждающего действия среды.
Диаметр пятна охлаждения D0, на котором происходит теплообмен со средой, определяется зависимостью
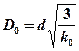 (5.17)
(5.17)
Наибольшая плотность стока теплоты I1 определяется в соответствии с формулой (5.2), если в нее подставить максимальную температуру:
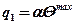 , (5.18)
, (5.18)
где α – коэффициент теплоотдачи,
Θmax – наибольшая температура на площадке теплообмена при совместном действии источника I и стока I1.
Эта температура может быть определена как
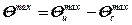 , (5.19)
, (5.19)
где 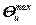 – максимальная температура, возникающая на площадке теплообмена под действием источника I, если охлаждение не применяется,
– максимальная температура, возникающая на площадке теплообмена под действием источника I, если охлаждение не применяется,
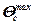 – снижение температуры за счет стока части теплоты в среду.
– снижение температуры за счет стока части теплоты в среду.
Максимальные величины температур можно определить, используя инженерную методику.
Температуру 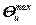 рассчитываем в соответствии с методикой, т.е.
рассчитываем в соответствии с методикой, т.е. 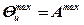 ,
,
где Аmax – произведение сомножителей в формуле (4.1) при известном коде задачи. При расчете 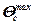 величина максимальной плотности теплоотдачи q1 принимается по формуле (5.18), т.е.
величина максимальной плотности теплоотдачи q1 принимается по формуле (5.18), т.е.
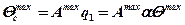 .
.
Таким образом, подставляя в формулу (5.19), имеем
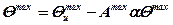 .
.
Откуда 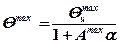 (5.20)
(5.20)
Аналогична и формула для расчета средних температур
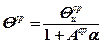 (5.21)
(5.21)
При расчете максимальных и средних температур по формулам (5.20) и (5.21) следует иметь в виду, что определение сомножителей для источника I и стока I1 должно производиться в соответствии с кодами их тепловой задачи и их характерными размерами.
Приведенные формулы могут быть использованы при решении балансовых задач. Для иллюстрации методики расчета рассмотрим предыдущую задачу, несколько видоизменив ее условие.
Задача.
Наружную поверхность заготовки из стали 20ХН3А упрочняют выглаживанием сферическим индентором из стали ШХ15 радиусом R=10мм (рис. 5.3). Скорость движения заготовки v = 1м/с; сила прижима индентора к заготовке P = 1000 Н. Коэффициент трения между заготовкой и индентором f = 0,12; диаметр пятна контакта d = 1мм. В зону обработки подается струя технологической жидкости на водной основе с расходом Qж = 10 л/мин и температурой 20°С из сопла диаметром dc = 5 мм. Рассчитать среднюю температуру на поверхности контакта.
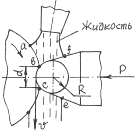
Рис. 5.3 – Процесс выглаживания поверхности с охлаждением жидкостью.
Чем отличается задача от рассмотренной ранее? В структурной схеме должен быть показан сток теплоты в жидкость с поверхности индентора. На поверхности заготовки сток теплоты в жидкость незначителен, поскольку теплообмен с заготовкой ниже точки с не влияет непосредственно на температуру контактной площадки, а на участке ав теплообмен незначителен вследствие малого различия между температурой жидкости и заготовки. Сток теплоты в жидкость с поверхности индентора на участке fe можно принять распределенным по нормальному закону. Структурная схема имеет вид (рис. 5.4).
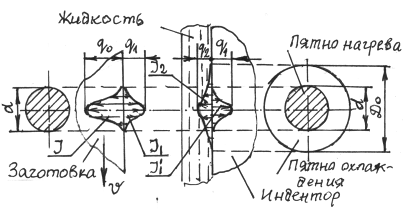
Рис. 5.4 – Структурная схема теплообмена с учетом охлаждения струей жидкости.
По сравнению с задачей, рассмотренной ранее, на структурной схеме показан сток теплоты с индентора I2 в охлаждающую жидкость на круге диаметром D0. Остальные допущения остаются теми же.
Код тепловой задачи для заготовки остается таким же, т.е.
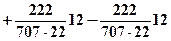 .
.
Код тепловой задачи для индентора включает кроме кода источника I11 также код стока теплоты I2, составленный аналогично
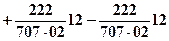 .
.
Решение.
1. Выписываем из предыдущего решения задачи рассчитанные зависимости температуры для заготовки и индентора (без учета охлаждения):
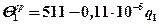 ;
; 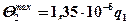 ;
; 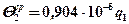 .
.
2. По формуле (5.16) определяем параметр
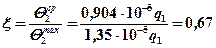
3. По формуле (5.15) определяем коэффициент сосредоточенности
к0 = 2,8(1 – ξ) = 2,8(1 – 0,67) = 0,924
4. По формуле (5.17) определяем диаметр пятна охлаждения
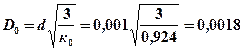 м.
м.
5. Определяем коэффициент теплоотдачи при вынужденной конвекции из критериального уравнения (5.12)
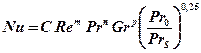
5.1 Принимаем сомножитель 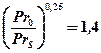
5.2 Определяем скорость потока жидкости, вытекающей из сопла
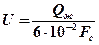 (м/с),
(м/с),
где Qж – расход жидкости, л/мин;
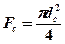 -площадь сечения сопла, мм2
-площадь сечения сопла, мм2
dc – диаметр сопла, мм.
Тогда 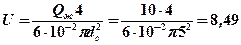 м/с.
м/с.
5.3 Приняв диаметр пятна охлаждения D0 за характерный размер и температуру Θ0 = 20°C как определяющую для жидкости, определяем критерий Рейнольдса по формуле (5.6)
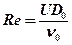
Справочные данные: принимаем для жидкости на водной основе и при температуре 20°С (приложение)
ν0 = 1,006·10 –6 м2/с 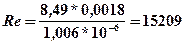 .
.
5.4 По формуле (5.7) определяем критерий Прандтля
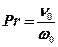
Справочные данные для принятых условий:
ω0 = 14,3·10 –8 м2/с 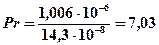
5.5 По формуле (5.8) определяем критерий Грасгофа 
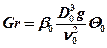
Справочные данные для принятых условий: β0 = 1,81·10 –4 1/°С
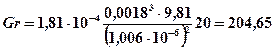
5.6. По формуле (5.12) определяем критерий Нуссельта
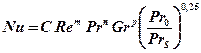
По таблице (5.2) выбираем при поперечном обтекании
Re > 1000 – C = 0,28, m = 0,6; n = 0,36; p = 0.
Nu = 0,28·152090,6·7,030,36·204,650·1,4 = 255
5.7. Из формулы (5.5) определяем коэффициент теплоотдачи
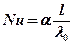 , откуда
, откуда 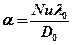 .
.
Справочные данные для принятых условий: λ0 = 59,9·10 –2 Вт/м°С.
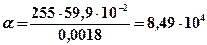 Вт/м2°С.
Вт/м2°С.
6. Используя инженерную методику, ведем расчет средней температуры на контактной площадке индентора от совместного действия источника I11 и стока I2. Значение средней температуры от действия источника I11 получено в предыдущем решении задачи
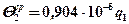
Определяем среднюю температуру от действия стока I2
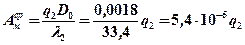 ,
,
(λ2 – коэффициент теплопроводности материала индентора)
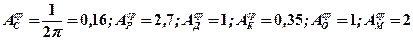
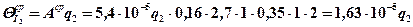 .
.
7. Определяем среднюю температуру на площадке контакта индентора по формуле (5.21)
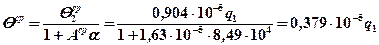
8. Решаем балансовую задачу распределения теплоты между деталью и индентором. Из предыдущего решения
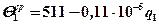
Принимаем условие 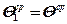 тогда 511 – 0,11·10 –5q1 = 0,379·10 –5q1
тогда 511 – 0,11·10 –5q1 = 0,379·10 –5q1
откуда 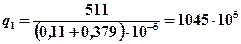 Вт/м2.
Вт/м2.
9. Рассчитываем среднюю температуру на площадке контакта
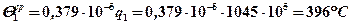 .
.
В предыдущем решении задачи средняя температура контакта без подачи охлаждающей жидкости составила 455°С, т.е. на 60° больше. Следует отметить, что рассчитанные температуры, как указывалось ранее, являются избыточными, т.е. они должны отсчитываться от температуры окружающей среды.
Вопросы для самопроверки
1. Перечислите основные уравнения, входящие в систему, решение которой позволяет определить коэффициент теплоотдачи.
2. Что такое характерный размер твердого тела и как его выбирают?
3. Что такое определяющая температура? Почему следует знать, для какой определяющей температуры написано критериальное уравнение?
4. В чем различие процессов теплообмена при естественной и вынужденной конвекции?
5. В каком случае коэффициент теплоотдачи от поверхности нагретой плиты в спокойный воздух больше: если она поставлена на короткое ребро или на длинное?
Задачи
1.  Шпиндельная бабка станка имеет размеры, показанные на рисунке. При длительной работе средняя температура поверхностей равна ΘS = 32°С. Пользуясь методикой ЭНИМС, определить суммарную мощность теплоотдачи поверхности бабки в атмосферу.
Шпиндельная бабка станка имеет размеры, показанные на рисунке. При длительной работе средняя температура поверхностей равна ΘS = 32°С. Пользуясь методикой ЭНИМС, определить суммарную мощность теплоотдачи поверхности бабки в атмосферу.
Рис. 5.5 – Схема шпиндельной бабки
Справочные данные для воздуха при температуре 20 °С:
β0 = 34,1·10 –4 1/°C; ν0 = 15,06·10 –6 м2/с; λ0 = 2,59·10 –2 Вт/м°С.
2. Рабочий орган станка перемещается двумягоризонтальными винтами наружным диаметром d0 = 63 мм и внутренним диаметром резьбы dP = 53 мм длиной 2000 мм. Средняя температура винтов 40 °С, температура воздуха 20 °С. Пользуясь методикой ЭНИМС, определить количество теплоты, отведенной с поверхности винтов при естественной конвекции за время 10 минут.
Справочные данные для воздуха при температуре 20°С:
β0 = 34,1·l0 –41/°C; ν0 = 15,06·10 –6 м2/с; λ0 = 2,59·10 –2 Вт/м°С.
3. Гидравлический бак гидропривода имеет размеры, показанные на рисунке. Средняя температура стенок бака ΘS = 55°С. Температура окружающей среды Θ0 = 20°С. Размеры бака – а = 400 мм, b = 600 мм., h = 400 мм. Пользуясь методикой ЭНИМС, определить суммарную мощность теплоотдачи с поверхности вертикальных стенок бака в атмосферу. Конвекцию считать естественной.

Для воздуха:
β0 = 34,1·l0 –41/°C; ν0 = 15,06·10 –6 м2/с; λ0 = 2,59·10 –2 Вт/м°С.
Рис. 5.6 – Схема гидравлического бака
4. Сливной трубопровод гидропривода имеет длину 1,5 м и диаметр d = 30 мм и расположен вертикально. Средняя температура стенок трубопровода 60°С. Температура окружающего воздуха 20°С. Пользуясь методикой ЭНИМС, определить мощность теплоотдачи с поверхности трубопровода в атмосферу при естественной конвекции (трубопровод можно принять как вал).
Для воздуха:
β0 = 34,1·l0 –41/°C; ν0 = 15,06·10 –6 м2/с; λ0 = 2,59·10 –2 Вт/м°С.
Дата добавления: 2020-06-09; просмотров: 540;











