Окружной к.п.д. осевой турбины

Окружной к.п.д. есть отношение окружной работы 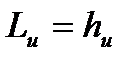, совершаемой рабочим телом на лопаточном венце, к располагаемой энергии L₀, приходящейся на данную ступень и характеризуемую величиной теплоперепада h_а, срабатываемого на ступени

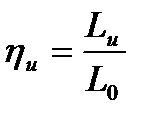
Как известно, по уравнению Эйлера секундная работа 1 кг. массы пара на рабочем венце турбинной ступени, т.е. окружная работа равна

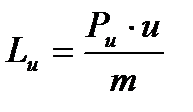
где, окружное усилие на среднем диаметре рабочего колеса Р_u может быть найдено через проекции относительных скоростей по уравнению

Тогда

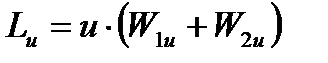
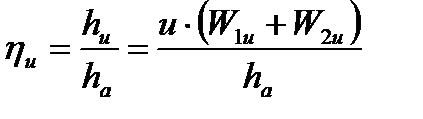
Для турбины с любой степенью реактивности

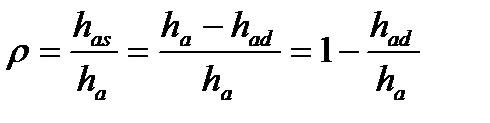имеем, что

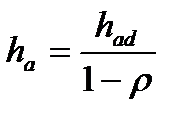или, учитывая 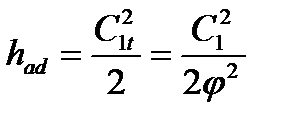найдем

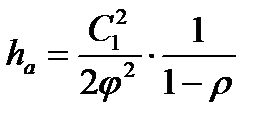
Тогда

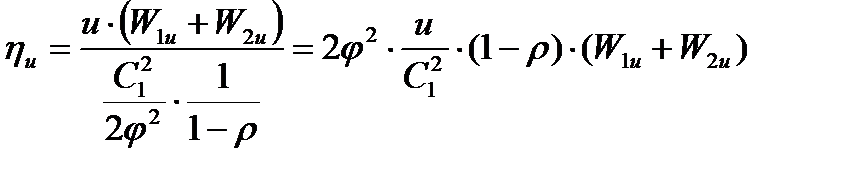
Учитывая, что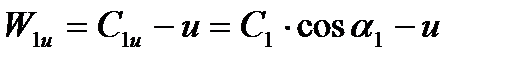

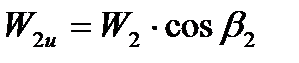
Получим

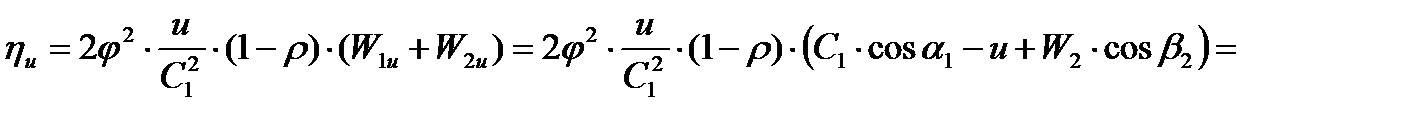
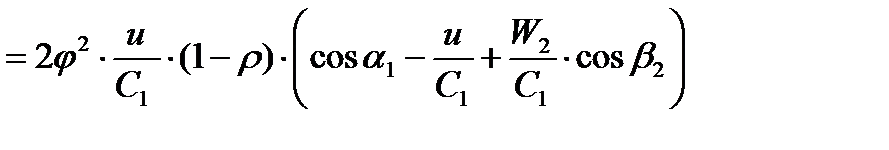(1)

Из уравнения (1) для активной ступени ρ = 0 следует

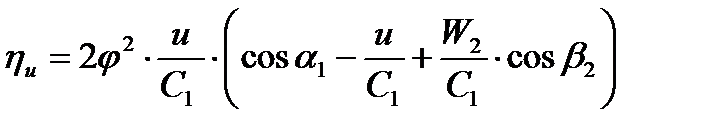
но 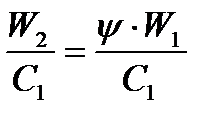или умножая на 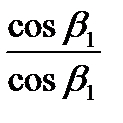найдем

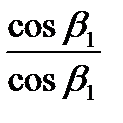
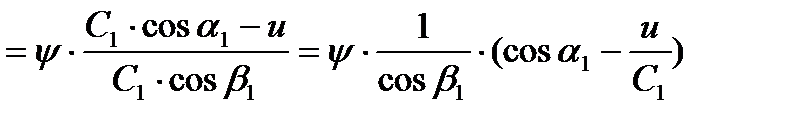
И тогда

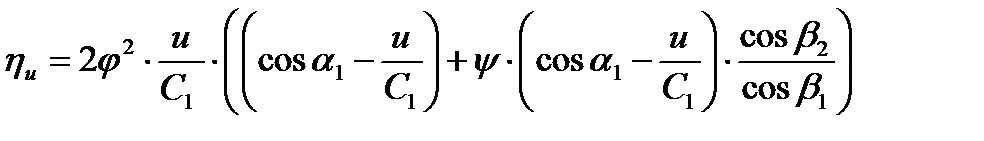или

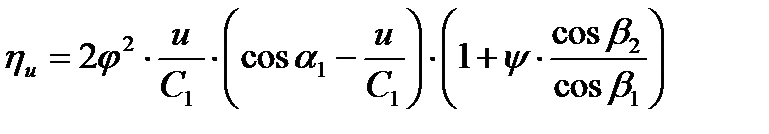- формула Банки

Из рассмотренной формулы видно, что η_u зависит:

от угла α₁, чем меньше угол α₁, тем больше к.п.д. Но уменьшение α₁, при заданной окружной скорости, вызывает уменьшение угла β₁, а, следовательно возрастание потерь от кривизны потока, т.е. уменьшение коэффициента ψ. Наивыгоднейший угол α₁ ≈ 14-20°

от угла β₂ – чем меньше угол, тем больше η_u. Но с уменьшением β₂ уменьшается коэффициент ψ, поэтому обычно β₂ = β₁ – (3° ÷ 10°) и как максимум делают β₂ = β₁

от отношения u/С₁. Это отношение имеет самое существенное влияние на η_u и носит название «характеристики активных турбин».

При заданных профилях сопел и лопаток, т.е. при φ - const, ψ - const, β₁ и β₂ – const, η_u будет зависеть только от выражения

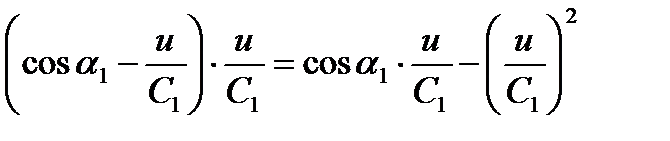
Беря от этого выражения первую производную и приравнивая ее к нулю, найдем величину наивыгоднейшего отношения u/С₁, при которой η_u будет максимальным

;

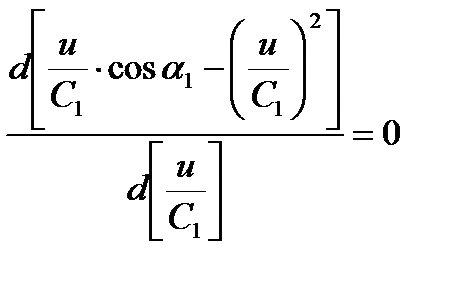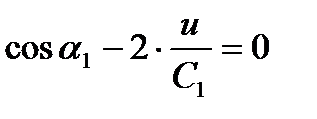
Откуда

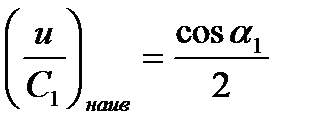
При .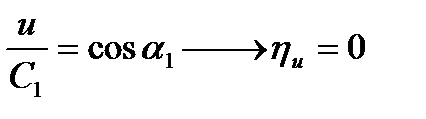

Здесь 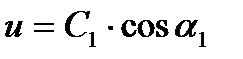и входной треугольник имеет вид

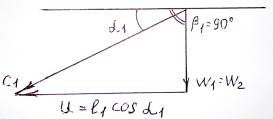
Но при выводе уравнения Банки, мы заменили условие, что 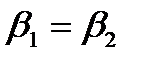и 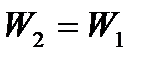и тогда получили, что скорость 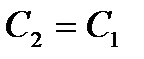и направление векторов скорости и 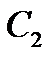совпадают, т.е. абсолютная скорость потока не претерпевает изменений как по величине, так и по направлению. Работа такой ступени равна нулю. В то же время из треугольников скорости видно, что при заданном угле α₁ и заданной величине скорости при изменении отношения u/С₁ будет изменяться и величина угла 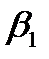, т.е. направление вектора 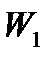, и форма профиля (при заданных вначале условиях 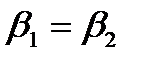) будет различной для каждого отношения u/С₁.

В действительности форма профиля выбирается для 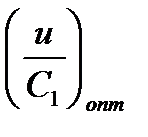и при изменения отношения u/С₁ остается неизменной.

Если подставить отношение 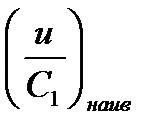в уравнение Банки и положив 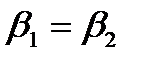получим

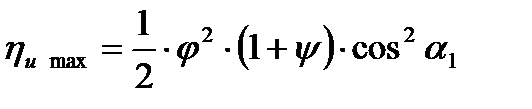
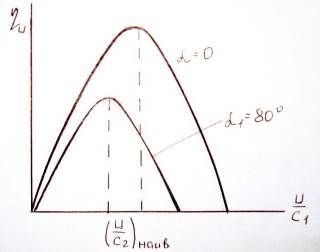
На основании уравнения Банки можно построить кривые зависимости η_u от отношения u/С₁.

Из уравнения имеем, что

при u/С₁ = 0 → η_u = 0

при u/С₁ = cosα₁ → η_u = 0

при u/С₁ = cosα₁/2 → η_u = η_max