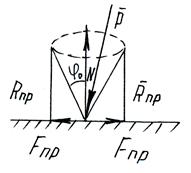
Равновесие при наличии трения.
Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наибольшего значения 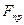 .
.
Реакция 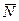 и
и 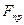
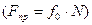 .
.
Составляют обычные уравнения равновесия и решают их.
Расчет ферм.
Фермой называется геометрически неизменяемая шарнирно-стержневая конструкция.
Если оси всех стержней лежат в одной плоскости, то такую ферму называют плоской.
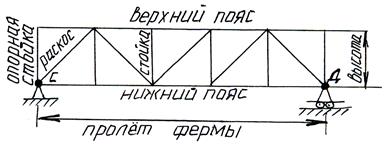 А,В-узлы фермы
А,В-узлы фермы
С,D-опорные узлы
Все шарниры, соединяющие стержни фермы предполагаются идеальными, т.е. без трения, а все внешние силы – приложенными в узлах фермы, т.е. все стержни испытывают лишь растяжение или сжатие (вес стержней не учитывают).
1 способ расчета ферм – (определение опорных реакций и усилий - способ вырезания узлов в стержнях).
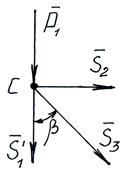
Этот способ сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние реакции и реакции стержней и составляют уравнения равновесия сил, приложенных к каждому узлу. Условно предполагают, что все стержни растянуты (реакции стержней направлены от узлов).
Если в вычислениях получается знак «–», то соответствующий стержень сжат.
Найденные реакции стержней равны по модулям внутренним усилиям в стержнях.
Последовательность рассмотрения узлов определяется обычно условием, что число неизвестных сил, приложенных к узлу не должно превышать число уравнений равновесия.
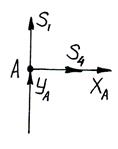
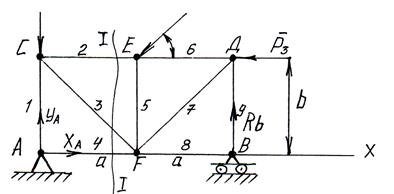 Пример:
Пример:
Определим реакции опор:
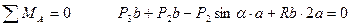
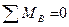
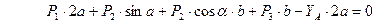
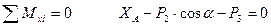
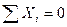
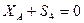
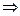
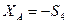
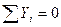
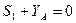
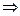
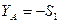
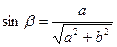
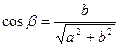
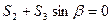
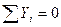
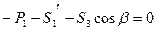
2 способ расчета ферм: метод Риттера (метод сечений).
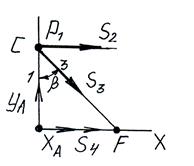 Ферму мысленно разделяют на 2 части сечением и рассматривают равновесие одной из частей (сечение проводят так, чтобы число неизвестных не превышало трех). Действие отброшенной части заменяют силами – реакциями соответствующих стержней, направляя их вдоль стержней от узла, т.е. считая стержни растянутыми.
Ферму мысленно разделяют на 2 части сечением и рассматривают равновесие одной из частей (сечение проводят так, чтобы число неизвестных не превышало трех). Действие отброшенной части заменяют силами – реакциями соответствующих стержней, направляя их вдоль стержней от узла, т.е. считая стержни растянутыми.
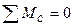
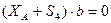
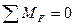
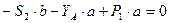
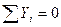
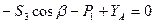
Метод Риттера удобно использовать для проверочных расчетов.
Лекция 9.
Дата добавления: 2016-06-29; просмотров: 1689;











