Критическая частота вращения невесомого вала с одним диском

Рассмотрим действие центробежной силы на вал с одним диском (вал располагается вертикально для того, чтобы исключить прогиб под действием собственной массы диска, а действие центробежной силы рассмотреть в чистом виде).

Центр тяжести 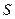неподвижного вала с диском 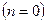расположен на расстоянии 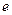от его оси (рис. 5.5. а). Появляющаяся при вращении ротора центробежная сила 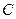вызывает прогиб у вала, величина которого зависит от силы 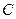, размеров и материала вала, а также от расположения диска относительно опор. Центробежная сила, увеличивающаяся с повышением частоты вращения, является периодической силой, приложенной к упругой балке (валу) и вызывающей гармонические колебания системы. Она уравновешивается упругой силой 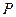, которая пропорциональна прогибу .

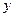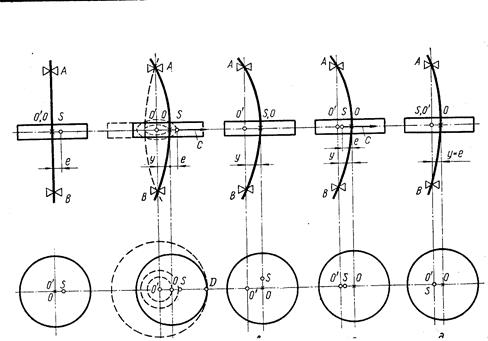
5.5 Положение центра тяжести диска при различной частоте вращения

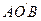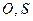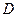Вращение вала происходит вокруг вертикальной оси (рис. 5.5. б), где показаны траектории точек и вокруг центра вращения (точки ).

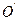Уравнение равновесия упругой системы имеет вид

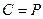. (5.6)

Центробежная сила

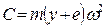, (5.7)

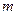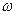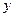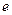где - масса диска, кг; - угловая скорость, рад/с; и , м.

Упругая сила

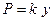, (5.8)

где 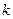- сила упругости, равная силе, вызывающей прогиб вала в 1 см, но противоположно ей направленная.

Подставляя значение величин 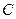и 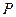в (5.6), получим

,

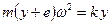откуда

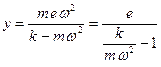. (5.9)

Следовательно, с увеличением угловой скорости 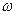(круговой частоты вынужденных колебаний ротора) прогиб 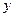(амплитуда вынужденных колебаний вала) возрастает и при некотором значении 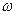величина .

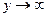Из теории колебаний упругих систем известно, что при резонансе (совпадении частот собственных и вынужденных колебаний упругой системы) амплитуда колебаний теоретически равна бесконечности 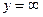, то есть вал должен сломаться.

Из (5.9) следует, что

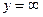при .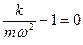

Отсюда резонансная круговая частота, или, как ее иначе называют, критическая угловая скорость вращения

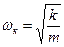, (5.10)

а критическая частота вращения ( )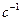

.

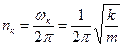Подставляя значение массы 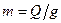, получим

, (5.11)

где 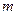, кг; 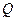- сила тяжести диска; 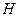; 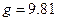м/с².

В действительности при критической частоте вращения возникают резонансные колебания, но вал сразу не ломается вследствие действия сил сопротивления. К ним относятся внутренние силы трения материала вала, трение поверхности ротора об окружающую среду и трение в подшипниках. Амплитуда колебаний при резонансе возрастает тем меньше, чем больше коэффициент сопротивления.

Работа турбины при критической частоте вращения сопровождается значительной вибрацией и при длительной работе может привести к аварии. Если быстро перейти критическую частоту вращения, то есть повысить круговую частоту вынужденных колебаний по сравнению с круговой частотой собственных колебаний, то малая длительность перехода через критическую частоту вращения обусловит развитие вибрации. При очень быстром переходе можно добиться, что резонансные колебания не усилятся, и вал будет работать без заметных колебаний. При относительно медленном переходе критической частоты вращения резонансные колебания появятся, но по мере удаления от критической частоты вращения они будут затухать.

Подставим значения 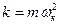из (5.8) в (5.7), тогда

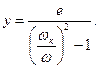(5.12)

Это выражение положительно при 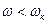и отрицательно при 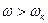. Угловая частота вращения 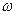представляет собой круговую частоту вынужденных колебаний вала, а 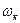- круговую частоту собственных колебаний.

Используя выводы теории колебаний, относящиеся к сдвигу фаз между собственными колебаниями (характеризуемыми прогибом 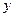) и возмущающей (центробежной) силой, определяемой направлением эксцентриситета 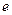, можно записать уравнение сдвига фаз для колебаний вала, обозначив 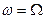и .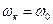

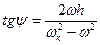. (5.13)

Зависимость 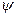от отношения частот 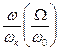построенная по (5.13) для различных значений коэффициента затухания 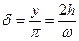, называется фазовой характеристикой (рис. 5.6). Вынужденные колебания всегда отстают по фазе от вынуждающей силы, причем величина отставания 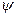лежит в пределах от 0 до 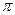. С увеличением 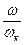сдвиг фаз 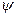постепенно увеличивается. В интервале 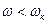угол 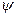положителен и меньше 90⁰. В момент резонанса, то есть при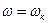 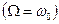, сдвиг фаз 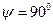(происходит опрокидывание фазы). При дальнейшем увеличении 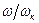когда 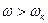, изменение сдвига фаз происходит замедленно в интервале .

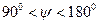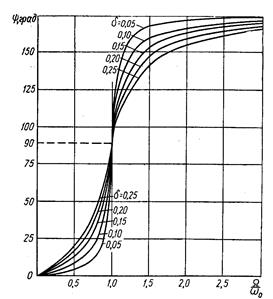
Рис. 5.6 Фазовые характеристики затухающих колебаний

Коэффициент затухания 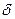влияет на изменение сдвига фаз 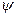следующим образом:

- при 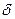, стремящемся к нулю, кривые стремятся к предельной кривой, имеющей разрыв в момент резонанса;

- при увеличении 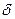сдвиг фаз в интервале 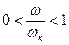происходит быстрее, а в интервале 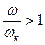медленнее.

Если коэффициент 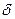мал и частота вынужденных колебаний значительно больше частоты собственных колебаний 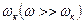, то угол сдвига фаз 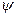приближается к 180⁰ (рис. 5.5. г). Последнее следует также из уравнения (5.13), в котором при 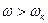знаменатель становится отрицательным, следовательно, отрицательным должен быть и эксцентриситет 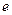. Повторив доказательство для угловой скорости больше критической ( 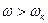), как и в случае 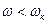получим

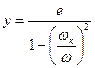. (5.14)

Отсюда следует, что с увеличением угловой скорости 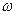величина прогиба 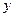уменьшается, при 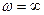становится равной эксцентриситету 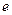. Следовательно, опасными для турбины является частоты вращения, близкие к критической. При частоте вращения, достаточно удаленной в обе стороны от критической частоты вращения, вал турбины работает без вибраций.

В паровых турбинах применяют так называемые жесткие и гибкие валы.

Жестким валом называется такой, у которого рабочая частота вращения (частота вынужденных колебаний), а гибким - у которого рабочая частота вращения выше критической.

Валы современных мощных турбоагрегатов выполняют гибкими. При пуске турбины с гибким валом для предотвращения развития резонансных колебаний проходить критическую частоту вращения необходимо за короткий промежуток времени. Для спокойной работы вала рабочая частота вращения должна отличаться от критической, по крайней мере, на 20…30%. Критическая частота вращения при гибких валах не должна отличаться от рабочей, так как при рабочей частоте вращения может наступить второй тон колебаний.

В турбинах с переменной частотой вращения обычно применяют жесткие валы, критическая частота вращения которых на 20…30% и более выше максимальной рабочей частоты вращения.

Рассмотрим колебания горизонтального вала рис. 5.7. Под действием силы тяжести диска 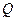, направленной вниз, вал прогибается на величину статического прогиба 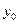. Центр тяжести 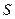расположен на расстоянии 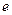от оси вала. При вращении вала с угловой скоростью 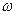(меньшей критической 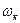) образуется центробежная сила 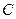, вызывающая прогиб его и направленная по радиусу от центра, поэтому вращение вала будет происходить вокруг упругой линии 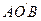(рис. 5.7. б).

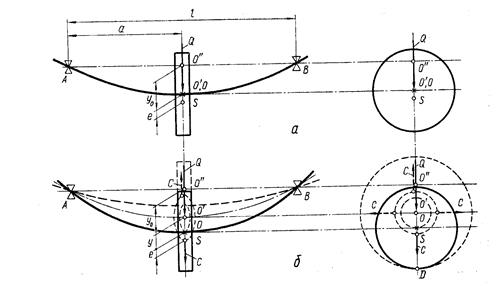
Рис. 5.7 Положение центра тяжести горизонтального вала

На рис. 5.7 б изображены траектории точек 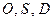, а также центробежная сила 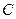в четырех положениях центра тяжести 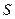при повороте вала на 90⁰. В этом случае центр тяжести описывает окружность радиусом 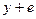, поэтому, как и в случае вертикального вала.

.

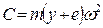Эта сила уравновешивается упругой силой 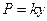. Отсюда следует, что все выводы, сделанные для вертикального вала, распространяются и на горизонтальный вал, а величина критической угловой скорости не зависит от расположения вала.

Изложенное выше подтверждается положением Стодола, что прогиб вала под действием массы диска не влияет на критическую частоту вращения, которая остается без изменения при вертикальном и горизонтальном положении вала. Найдем зависимость между статическим прогибом 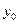и критической частотой вращения 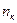. Статический прогиб 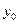можно определить как

,

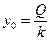отсюда

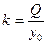. (5.15)

Подставляя значение 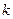в (5.12), получим (с^-1)

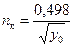. (5.16)

Таким образом, критическая частота вращения 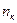изменяется обратно пропорционально корню квадратному из статического прогиба вала, то есть с увеличением прогиба вала 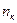уменьшается в квадрате.

Статический прогиб 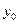зависит от жесткости ротора, длины вала, способа крепления его концов и характера распределения нагрузки. В общем случае уравнение статического прогиба в соответствии с уравнениями сопротивления материалов можно записать как

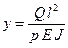, (5.17)

где 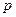- коэффициент, зависящий от способа крепления концов вала и характера нагрузки; 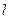- длина вала; 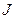- момент инерции вала.

Например, для вала, свободно лежащего на двух опорах с нагрузкой посередине 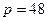; с диском, расположенным на расстоянии 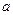от опоры (рис. 5.7 а).

.

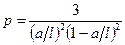Согласно (5.17) статический прогиб вала, а значит, и критическая частота вращения (5.16) в значительной степени зависит от длины вала, так как прогиб его пропорционален кубу длины 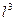. При расчете критической частоты вращения требуемое значение можно получить, изменяя диаметр вала .

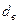Момент инерции вала

.

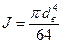Следовательно, статический прогиб вала, а значит, и критическая частота вращения значительно зависят от его диаметра. Например, если диаметр вала увеличить в два раза, то прогиб уменьшится приблизительно в 16 раз, а критическая частота вращения (5.16) увеличится приблизительно в четыре раза.

Критическая частота вращения вала постоянного сечения с
равномерно распределенной массой

Вал постоянного сечения с равномерно распределенной массой по длине (при 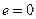) вращается, имея прогиб. Для определения его критической частоты воспользуемся дифференциальным уравнением колебаний призматического стержня, которое запишется в виде

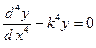(5.18)

где

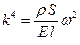. (5.19)

Здесь 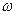- угловая скорость вращения; 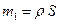- масса единицы длины вала.

Обще решение дифференциального уравнения (5.18), содержащее четыре произвольных постоянных, имеет вид

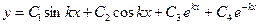. (5.20)

Учитывая граничные условия для вала, свободно лежащего на двух опорах, получаем систему однородных уравнений, при совместном решении которых определяются произвольные постоянные:

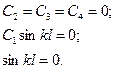(5.21)

Уравнение (5.21) удовлетворяется, если

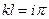(5.22)

где .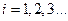

Из выражений (5.19) и (5.20) получим формулы для определения критической угловой скорости:

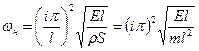, (5.23)

где 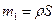- масса единицы длины; 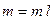- масса всего тела.

Окончательное уравнение упругой линии вала получаем из (5.20) при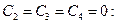

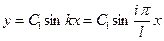. (5.24)

Следовательно, упругая линия при колебаниях весомого вала без дисков представляет собой синусоиду. При колебаниях:

а) 1-го тона 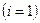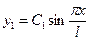- вал не имеет узловой точки (рис.5.8. а);

б) 2-го тона 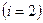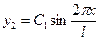- имеется одна узловая точка и на длине вала располагаются две полуволны (рис.5.8. б);

в) 3-го тона 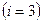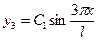- имеются две узловые точки и три полуволны (рис.5.8. в).

В противоположность случаю невесомого вала с одним диском, рассмотренного ранее, для вала постоянного сечения с равномерно распределенной массой получается бесконечно большое число критических скоростей 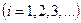. Отношение критических скоростей вращения при различных колебаниях для рассмотренного вала в соответствии с (5.24) составляет:

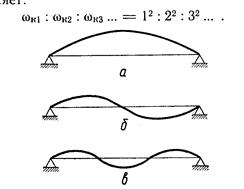
Рис. 5.8 Различные формы колебаний весомого вала без дисков:
а – 1-й тон; б – 2-й тон; в – 3-й тон

Критическая частота вращения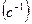

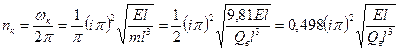, (5.25)

где 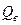- сила тяжести вала, Н; 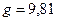м/с².

Прогиб вала под действием статической нагрузки от собственной массы

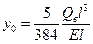. (5.26)

Учитывая (5.25) и (5.26), получим

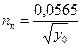. (5.27)