Расчет на прочность червячных передач
В червячных передачах, аналогично зубчатым, зубья червячного колеса рассчитывают на контактную прочность и прочность при изгибе. Как отмечалось выше (см. § 18.8), в червячных передачах кроме выкрашивания рабочих поверхностей зубьев велика опасность заедания, которое также зависит от величины контактных напряжений он. Поэтому для всех червячных передач расчет по контактным напряжениям является основным,определяющим размеры передачи, а расчет по напряжениям изгиба — проверочным.
Расчет по контактным напряжениям. Воснову вывода расчетной формулы для червячных передач положены те же исходные зависимости и допущения, что и при рассмотрении зубчатых передач (см. § 13.4).
Вывод формулы ведут для передачи с архимедовым червяком, у которой условия зацепления и несущая способность мало отличаются от других передач с линейчатыми червяками.
Наибольшее контактное напряжение в зоне зацепления по формуле Герца (2.13)
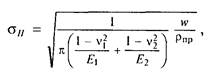
где Е1 и Е2 v1 и v2 — соответственно модули упругости и коэффициенты Пуассона стального червяка и бронзового или чугунного венца колеса (см. § 5.2);
w — нормальная нагрузкана единицу длины контактной линии. Эта нагрузка распределена неравномерно вследствие деформаций валов червяка и колеса, а также подшипников и корпуса передачи:

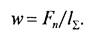
Здесь Fn — сила, нормальная к поверхности зуба червячного колеса и витка червяка и приложенная в полюсе зацепления. Согласно рис. 18.10, а
Fn= FJ(cos a cosψK);
lΣ — суммарная длина контактных линий в зацеплении червячной передачи. Согласно рис. 18.11 длина одной контактной линии прямо пропорциональна начальному диаметру червяка dwl и углу обхвата 28. Если учесть, что с увеличением угла ψк подъема витка длина линии контакта растет обратно пропорционально cos ψкто при коэффициенте εа перекрытия и минималь-
ном значении коэффициента ξ, колебания суммарной длины контактных линий получим
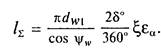
При средних значениях коэффициента ξ = 0,75, угла обхвата 2δ= 100° и коэффициента торцового перекрытия в средней плоскости сечения колеса εα = 2 суммарная длина контактных линий 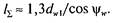
После подстановки получим
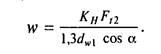
Здесь дополнительно введен коэффициент нагрузки КΗ = КΗβ КΗν учитывающий неравномерность распределения нагрузки в зоне контакта вследствие деформации деталей передачи (KHβ), а также внутренней динамики передачи (КΗν).
рпр — приведенный радиус кривизны профилей витков червяка и зубьев колеса в полюсе зацепления.
В осевом сечении профиль витка архимедова червяка прямолинейный (p1=°°, см. рис. 18.6), а зубья червячного колеса имеют эвольвен-гный профиль, поэтому приведенный радиус кривизны для червячной пары равен радиусу кривизны профиля зуба червячного колеса в полюсе зацепления (см. § 13.4):
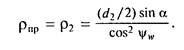
Подставив значения Е, v, w, рпр в формулу Герца и приняв а = 20°, ψw. = 10°, а также заменив значения Ft2 = 2- 103 T2/ d2; d2 = mz2, dw1 = m{q + 2x); m = 2aw /(z2 + q + 2x), получим формулу проверочного расчета червячных передач по контактным напряжениям:
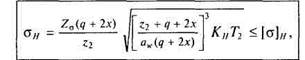
|
(18.28)
где σΗ—расчетное контактное напряжение в зоне зацепления, Н/мм2; аw — межосевое расстояние, мм; Т2 — вращающий момент на колесе, Н • м.
Значения коэффициента Za для червячных передач:
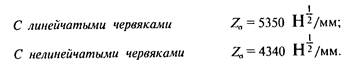
Червячные передачи с нелинейчатыми червяками имеют более благоприятное соотношение радиусов кривизны червяка и колеса, боль-тую суммарную длину контактных линий, что обусловливает их повышенную нагрузочную способность.
Червячные передачи работают плавно, бесшумно, поэтому вних пополнительные динамические нагрузки невелики. Хорошая приработка
зубьев колес к виткам червяков значительно уменьшает концентрацию нагрузки.
При обычной точности изготовления и выполнении условия жесткости червяка [см. формулу (18.34)] принимают: Кн= 1 при v2<3 м/с; Кн= 1,1...1,3 при v2 > 3 м/с, где v2 —окружная скорость червячного колеса.
Приняв из условия жесткости червяка q = Q,25z2, а также К„=1, х = 0 и решив зависимость (18.28) относительно а„, получим формулу проектировочного расчета червячных передач:

где аи, — межосевое расстояние, мм; [σ]Η—в Н/мм2; Т2 — в Нм.
Значения коэффициента Ка для червячных передач:
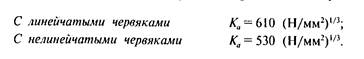
Полученное расчетом значение aw округляют в большую сторону до стандартного значения (см. § 18.4) или до ближайшего значения из ряда нормальных линейных размеров (см. § 27.4).
Расчет по напряжениям изгиба.Расчет зубьев червячного колеса на изгиб аналогичен расчету зубьев цилиндрических косозубых колес. В формулу (13.14) вводят поправки, связанные с выражением входящих в нее величин через параметры червячной передачи и учитывающие более высокую прочность зубьев червячного колеса на изгиб (на - 30 %) вследствие их дугообразной формы (см. рис. 18.11).
С учетом этих поправок при KF= Кн получают формулу проверочного расчета зубьев червячного колеса по напряжениям изгиба:

Дата добавления: 2020-05-20; просмотров: 632;











