Сложение гармонических колебаний

Реальные колебания чаще всего негармонические, носят более сложный характер. Но многие негармонические колебания можно представить в виде суммы гармонических колебаний.

а) сложение однонаправленных гармонических колебаний одинаковой частоты:

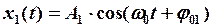и

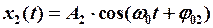
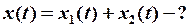
Для получения результата воспользуемся методом векторных диаграмм: любое гармоническое колебание графически можно изобразить в виде вращающегося против часовой стрелки вектора длиной, равной амплитуде колебания и имеющего в момент времени t = 0 угол наклона к некоторой оси ОХ, равный начальной фазе этого колебания.

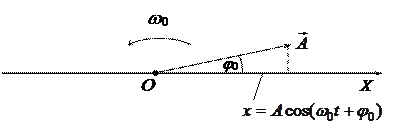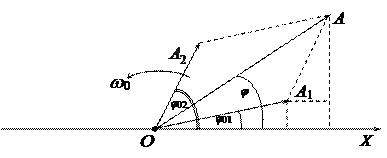Результирующее колебание будет гармоническим:

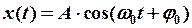
с той же частотой 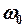, но с новой амплитудой А и новой начальной фазой 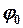, которые можно определить.

(12-1)

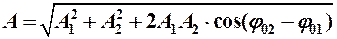
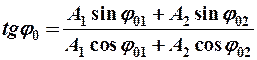
б) сложение однонаправленных колебаний с разными частотами:

- пусть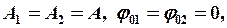

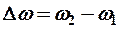
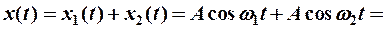
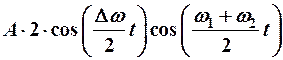
- если 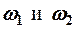близкие ( 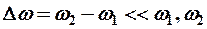), тогда

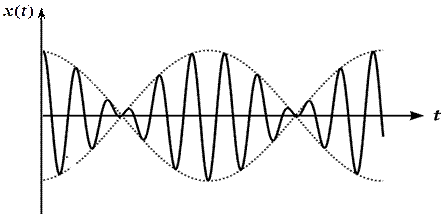
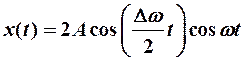(12-2)

Биения!

- если 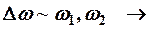результирующее колебание сложное!

в) сложение взаимноперпендикулярных гармонических колебаний одинаковой частоты:

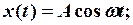
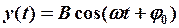
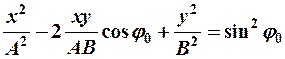(12-3)

-

-

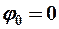
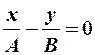
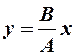
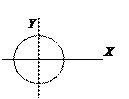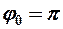
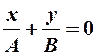
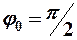
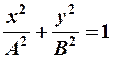- A = B = R.

г) сложение взаимноперпендикулярных гармонических колебаний с разными частотами:

- если частоты кратные друг другу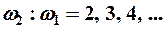

- фигуры Лиссажу !

- если частоты не кратные ® сложный негармонический процесс.