Координатный способ задания движения точки

Положение точки 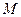по отношению к выбранной системе отсчета ХОY определяют ее декартовы координаты 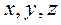(рис. 29).

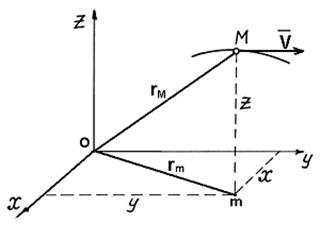
Рис. 29. Схема к координатному и векторному

способам задания движения точки М

На рис. 29 представлена система координат или системами отсчёта. Она широко используются в научных исследованиях, а на школьных уроках для формирования у учеников наглядных представлений об изучаемом предмете.

Уравнения движения точки в пространственной системе координат (рис. 29) в общем виде записываются так:

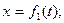(14)

(15)

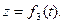(16)

Все законы классической механики работают в рамках основной аксиомы Естествознания – аксиомы Единства пространства, материи и времени. Математическая суть этой аксиомы выражается зависимостью координат объектов, движущихся в пространстве, от времени.

Когда точка движется по прямой линии, например, вдоль оси OX (рис. 29), то 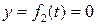и , и уравнение её движения записывается так

. (17)

Приведенные уравнения закона движения точки (14, 15 и 16) содержат переменный параметр - время 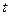, поэтому их называют параметрическими уравнениями движения точки. Расстояние от начала координат (точка О) до точки М определяется по формуле (рис. 29).

. (18)

Аналогично определяется расстояние от начала отсчёта (0) до проекции m точки М на плоскость XOY (рис. 29).

. (19)