Доходность финансовой операции. Простые проценты

Под финансовой операцией понимают любые операции по вложению, размещению, инвестированию временно свободных денежных средств или их эквивалентов с целью получения дохода.

Лицо, предоставляющее временно свободные средства является кредитором. Лицо, совершающее финансовые операции с этими средствами и берущее на себя обязательство вернуть через определенное время t эти средства, увеличенные на оговоренную сумму дохода, называют заемщиком.

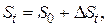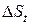Обозначим первоначальную сумму размещаемых кредитором средств через S₀, а сумму возвращаемую заемщиком после совершения финансовой операции через где - величина дохода, полученного от использования первоначальной суммы в течение времени t.

Доходность финансовой операции можно определить отношением:

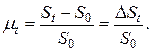(1.1)

Доходность финансовой операции оценивают в относительных величинах (1.1) или в процентах:

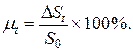
Сумма денежных средств, получаемая кредитором в конце финансовой операции, будет равна 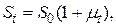где 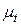- доходность в относительных единицах.

При принятии решения о вложении временно свободных денежных средств кредитор учитывает время t, через которое он получит их с доходом 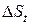; доходность 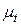финансовой операции, которую обещает заемщик; возможные риски, связанные с данной операцией.

Естественно кредитор будет рассматривать несколько вариантов финансовых операций, среди которых будет практически безрисковое размещение денежных средств на банковский депозит с гарантированной годовой доходностью t = 1 год.

Обозначим годовую доходность по банковским депозитным вкладам буквой i.

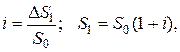
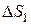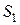где и - величина дохода, и общая сумма получаемая кредитором после истечения одного года вклада.

Величину i называют годовой процентной ставкой – это сумма, выплачиваемая кредитору в конце периода начисления 1 год за каждую единичную сумму (например, 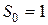тыс. руб.) занятую заемщиком в начале периода.

Простые проценты

Схема начисления простых процентов поясняется рис. 1.1.

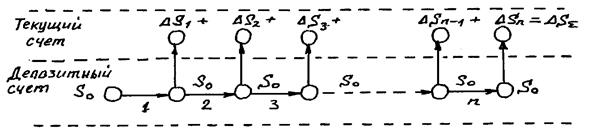
Рис. 1.1. Схема начисления простых процентов

Пусть первоначальная сумма, внесенная на депозит, равна 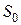при годовой процентной ставке i. Тогда наращенная за год сумма будет равна:

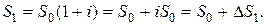
Если депозитный договор заключен на n-лет с фиксированной годовой процентной ставкой, при начислении дохода 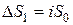по схеме простых процентов, то в конце каждого года этот доход переводится на текущий счет, а сумма, размещенная на депозите, остается постоянной равной .

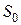На текущем счете банковская процентная ставка равна нулю Доходы, перечисляемые на текущий счет, могут по усмотрению кредитора или оставаться на текущем счете или изыматься для своих нужд.

Если депозитный договор заключен на n-лет, то в конце срока вклада кредитор получит сумму:

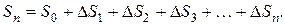
При постоянной годовой процентной ставке 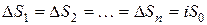и конечная наращенная за n-лет сумма будет равна:

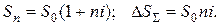(1.2)

Если процентная ставка изменяется год от года, то:

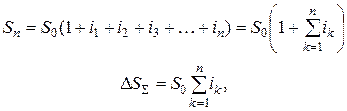(1.3)

где 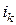- годовая процентная ставка в k-том году.

Если момент возврата ссуды является переменной величиной (например, депозитный вклад довостребования), то наращенная сумма в день выдачи ссуды определяется по формуле:

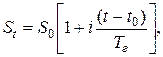(1.4)

где 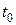- день вложения средств на депозит;

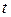- день возврата средств;

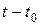- срок действия депозитного договора в днях;

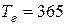- количество дней в году.

Если денежные средства в сумме 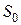по схеме простых процентов последовательно вкладываются на промежутки времени 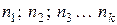дней с разными годовыми процентными ставками 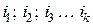, то наращенная сумма 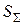за весь период времени 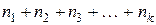будет равна:

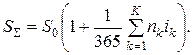(1.5)

Иногда депозитные договора заключаются с m-кратным начислением процентов в году. При 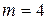, проценты начисляются и могут быть выплачены ежеквартально, при 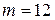- ежемесячно. В этом случае наращенная сумма на первом сроке выплаты процентов будет равна:

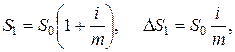
где m - кратность начисления процентов в году; i – годовая процентная ставка.

Тогда при сроке вклада 1 год проценты в размере 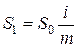будут начислены m раз, и наращенная сумма по истечения года будет равна:

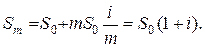
Отсюда следует, что при размещении средств по схеме простых процентов увеличение кратности выплат не приводит к увеличению наращенной суммы.

В соответствии с формулой (1.4) наращенная сумма в схеме простых процентов является линейной возрастающей функцией с увеличением срока вклада (см. рис. 1.3).

Сложные проценты

Получение наращенной суммы 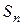при начислении процентов по схеме сложных процентов поясняется рис. 1.2.

Рис. 1.2. Наращение суммы вклада по схеме сложных процентов

При наращении по схеме сложных процентов происходит реинвестирование, или капитализация полученных процентов. Предположим, денежные средства 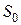вкладываются в банк на депозитный договор с капитализацией начисляемых процентов по годовой процентной ставке i на n-лет.

По истечении первого года наращенная сумма будет равна:

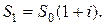
На втором году сумма депозитного вклада будет равна 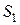и наращенная сумма по истечению второго года будет равна:

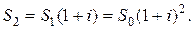
К концу n-го года действия депозитного договора наращенная сумма будет определяться формулой:

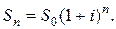(1.6)

Таким образом, последовательность наращенных сумм 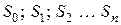является геометрической прогрессией с начальным членом 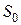и знаменателем прогрессии 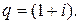Коэффициент пропорциональности 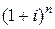между наращенной 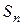и первоначальной 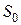суммами называется коэффициентом наращения. При определении наращенной суммы в произвольный момент времени t необходимо пользоваться формулой:

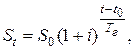(1.7)

где 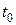- день вложения денежных средств на депозит;

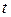- день окончания депозитного договора;

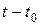- срок депозитного вклада в днях;

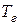- количество дней в году.

Суммарный доход 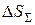, получаемый за весь срок депозитного вклада в соответствии с формулами (1.6) и (1.7) может быть представлен в виде:

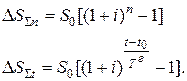(1.8)

Определим наращенную сумму при m-кратном начислении процентов в год. Если начисление сложных процентов происходит m-раз в году, то наращенная сумма при первом начислении процентов будет равна:

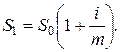
При втором начислении процентов:

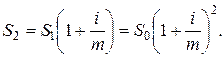
По истечении одного года при m-том начислении процентов наращенная сумма будет равна:

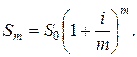(1.9)

Если депозитный договор с m-кратным начислением процентов и их капитализацией заключается на n-лет, то наращенную сумму можно определить по формуле:

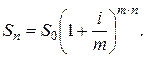(1.10)

Определим эффективную годовую процентную ставку 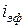при m-кратном начислении процентов с их капитализацией из равенства получаемых за год наращенных сумм:

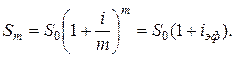
Отсюда для годовой эффективной процентной ставки получим:

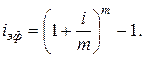(1.11)

Тогда формулу (1.10) для срока депозитного договора на n-лет при m-кратном начислении процентов можно записать в виде:

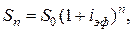(1.12)

где 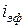- определяется формулой (1.11).

В соответствии с формулами (1.6), (1.7) и (1.12) наращенная сумма в схеме сложных процентов является показательной функцией. Сравнение наращенных сумм вычисляемых по схеме простых и сложных процентов (см. рис. 1.3) позволяет сделать следующие выводы:

1) при сроке вклада один год наращение по схеме простых и сложных процентов при одинаковых процентных ставках имеют одинаковый коэффициент наращения;

2) при сроке вклада меньше одного года коэффициент наращения по схеме простых процентов больше чем при схеме сложных процентов;

3) при сроке вклада больше одного года коэффициент наращения по схеме сложных процентов больше чем при схеме простых процентов;

4) при наращении по схеме сложных процентов m-кратное начисление процентов приводит к увеличению коэффициента наращения;

5) при наращении по схеме простых процентов m-кратное начисление процентов не влияет на коэффициент наращения.

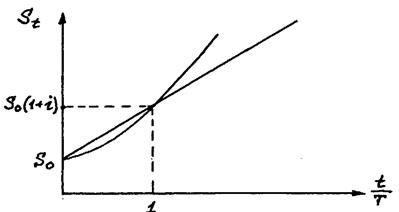
Рис. 1.3. Наращение по простой и сложной ставкам