Расчет на прочность.

Крепление двигателя необходимо рассчитывать на все случаи, предусмотренные нормами прочности, для чего необходимо определить нагрузки, соответствующие случаям нагружения.

Рама звездообразного ПД является дважды статически неопределимой, так как имеет два лишних стержня. Ввиду того, что она имеет плоскость симметрии, расчет можно упростить: все нагрузки разбить на группу симметричных и группу обратно симметричных. К первым относятся нагрузки, одинаковые по величине симметрично расположенные относительно плоскости симметрии конструкции, а также нагрузки, лежащие в этой плоскости. Ко вторым относятся одинаковые по величине нагрузки, расположенные с обеих сторон плоскости симметрии конструкции таким образом, что они превращаются в симметричные, если с одной стороны плоскости симметрии направление нагрузок изменить на обратное. В симметричных стержнях усилия от симметричных нагрузок равны по величине и знаку, а в обратно симметричных равны по величине и противоположны по знаку. Исходя из вышесказанного рама ПД двигателя превращается в однажды статически неопределимую.

При определении усилий в стержнях рамы для различных случаев нагружения расчет удобно вести по симметричным и обратно симметричным нагрузкам в общем виде. Сначала учитывают действие симметричных нагрузок, а затем — обратно симметричных.

Для проведения расчета как при действии симметричных, так и обратно симметричных нагрузок необходимо:

1) выбрать основную систему;

2) определить усилия S_p, возникающие в стержнях основной системы от действия заданной нагрузки;

3) найти усилия S_b возникающие в стержнях основной системы от единичных сил, приложенных по направлению лишних неизвестных в нарушенных связях;

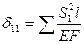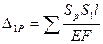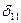4) вычислить перемещения в основной системе по формулам: , , где — перемещение по направлению хот X = 1; l, Е, F— длина, модуль упругости материала и площадь поперечного сечения стержня;

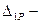перемещение по направлению x₁ от заданной нагрузки;

5) решить каноническое уравнение: ,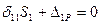

6) найти полное усилие в стержнях способом наложения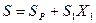

Перед этим необходимо провести вычисление косинусов углов, образуемых направлениями стержней и осями координат:

Расчет на действие симметричных нагрузок выполняется следующим образом. Выбирают основную систему. Для этого мысленно разрезают стержни 1—4 и 1'—4'. Так как усилия в этих стержнях одинаковы по величине и знаку, то обозначим их через Х₁ и направим от двигателя, считая стержни растянутыми.

Находим усилия S_p в остальных шести стержнях основной системы от заданной нагрузки, предполагая стержни растянутыми и считая, что в симметричных стержнях усилия равны. Составив условия равновесия, имеем:

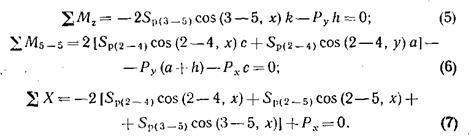
Из формулы (5) определяем усилие :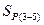

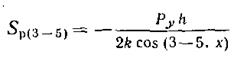
Усилие 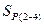находим из уравнения (6):

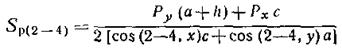
Последнее неизвестное усилие определяем из уравнения (7):

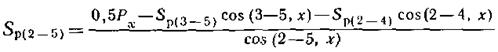
После этого необходимо произвести проверку правильности решения задачи. Если усилия в стержнях определены верно, то сумма проекций всех сил на ось у должна быть равна нулю.

При нагружении основной системы единичными силами X₁ = 1 внешние силы Р_х и Р_у предполагаем равными нулю. Тогда уравнения равновесия примут вид:

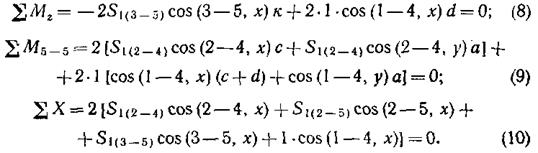
Решая эти уравнения, находим:

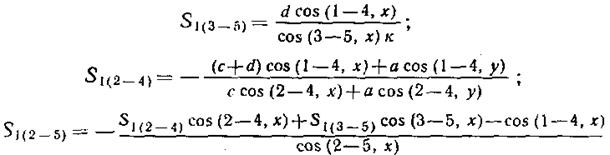
Правильность решения задачи контролируется равенством нулю суммы проекций всех сил на ось у. Результаты расчета сводим в таблицу, по которой производится расчет коэффициентов 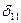и 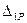, а также действительных усилий, возникающих в стержнях от симметричной нагрузки:

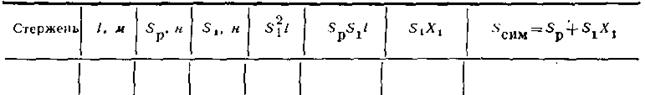
Следующим этапом является расчет крепления при действии обратно симметричных нагрузок Р_г, М_х, М_у и M_z.

Основную систему выбираем прежней. Как и ранее, мысленно отсекаем переднюю часть силовой установки и составляем условия равновесия для отсеченной части. Слева от плоскости симметрии стержни считаем растянутыми, справа — сжатыми. Удовлетворяя условиям равновесия системы, получаем три уравнения с тремя неизвестными силовыми факторам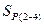и , и 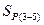. Решение указанных уравнений даст выражения для определения искомых усилий (методика составления уравнений и их решения аналогична приведенной ранее при рассмотрении действия симметричных нагрузок).

Затем нагружаем основную систему силами Х₁ = 1 и вычисляем усилия в стержнях, предполагая внешние нагрузки равными нулю. Удовлетворяя условиям равновесия, определяем , 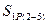и 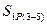. Составляем вспомогательную таблицу, по которой рассчитываем усилия в стержнях:

Полные усилия в стержнях при действии на крепление любых произвольных нагрузок находим как сумму двух усилий от действия симметричных и обратно симметричных нагрузок:

Необходимо отметить, что формулой (11) можно пользоваться только в тех случаях, когда напряжения в стержнях не превышают предела пропорциональности и ни один из сжатых стержней не теряет устойчивости. Предполагается, что при действии эксплуатационных нагрузок эти условия выполняются.

Если отдельные стержни начинают работать в области пластических деформаций или сжатые стержни теряют устойчивость, то действие каждого такого стержня на систему крепления заменяется силой S_i, равной усилию в стержне, при котором наступает текучесть материала, или критической силе (при сжатии). Усилие S, в этих случаях считается заданной внешней нагрузкой, и расчет далее ведется описанным выше методом.

Расчет крепления ТВД ферменного типа ведется аналогичным образом.

Расчет крепления ТВДферменно-балочного типа может быть проведен при предположении, что балка 5 от цапфы двигателя до крепления к внутреннему подкосу 6 представляет собой стержень. Так как стержень 6 не связан непосредственно с двигателем, то двигатель крепится шестью стержнями и система статически определима. Составив уравнение моментов относительно передней цапфы крепления двигателя, а также сумму проекций всех сил на оси х и у и приравняв проекции нулю, можно определить усилия в стержнях и балке. Полученное усилие в балке в точке соединения ее с внутренним подкосом раскладывается по двум направлениям — по внутреннему подкосу 6 и по балке от точки крепления подкоса к шпангоуту гондолы. После этого они легко находятся. При действии силы P_z балка работает на изгиб.

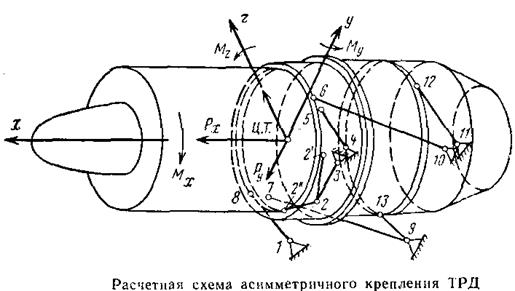
Определение усилий в стержнях асимметричной фермы крепления ТРДнесколько сложнее, так как для этого необходимо решать большее число уравнений. Наименьшее количество стержней m пространственной фермы с плоскими узлами определяется уравнением:

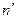где и 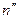— количество пространственных и плоских узлов соответственно.

В рассматриваемой ферме 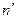=0 и 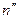=1. Следовательно, минимальное количество стержней должно быть равно восьми. В действительности ферма имеет девять стержней. Рассекаем ферму так, чтобы стержни 2—2' и 2—2" остались с двигателем, тогда ферма будет иметь один лишний стержень. В качестве лишнего можно принять любой из стержней. Если предположить, что лишним является стержень 11—12, то можно найти усилия в остальных шести стержнях (1—8, 3—2, 4—5, 10—6, 9—7 и 9—13) основной системы от внешних нагрузок. Для этого необходимо составить и решить шесть уравнений равновесия. В дальнейшем определяем усилия в стержнях от единичной нагрузки, действующей в лишнем стержне, и после этого полные усилия в стержнях. Зная усилие истержне2—3, можно определить усилия в стержнях 2—2' и 2—2", рассматривая равновесие плоского узла 2.