Адаптивные процедуры

Существенно уменьшить, а в ряде случаев и упростить требуемую от ЛПР информацию можно, если попытаться определить наилучшую или наиболее предпочтительную альтернативу, не восстанавливая функцию полезности. Процедуры, реализующиеэту идею, используют подход, основанный на выявлении предпочтений одновременно с исследованием допустимого множества альтернатив.

Одна из идей, используемая здесь, сводится к тому, чтобы выбрать любой известный алгоритм математического программирования, который хорошо зарекомендовал себя при решении скалярных оптимизационных задач, и распределить функции между человеком и ПЭВМ таким образом, чтобы в результате их взаимодействия обеспечивалось получение всей необходимой для работы алгоритма информации. Например, если мыстремимся реализовать алгоритм градиентного типа, то ЛПР выступает в качестве своеобразного измерительного устройства, выдающего информацию, на основе которой можно определять градиент функции полезности в каждой точке. При реализации некоторых других методов, например, процедуры Нелдера-Мида от ЛПР требуется «всего лишь» проводить парные сравнения альтернатив.

Часто оказывается, что ЛПР не в состоянии отвечать на вопросы, которые предусматриваются этими процедурами без значительных и частых ошибок. Фактически эти процедуры пытаются приблизить возможности человека к потребностям вычислительной системы.

В последнее время довольно интенсивно разрабатывается другой подход к построению адаптивных процедур, ориентированный, прежде всего, на возможности ЛПР. Здесь, прежде всего, выявляются типы вопросов, на которые ЛПР может отвечать без особых затруднений и с достаточно высокой точностью, а затем на основеэтих вопросов строится процедура выявления предпочтений одновременно с исследованием множества альтернатив.

Рассмотрим,например, известную процедуру Соболя-Статникова [43]. Метод заключается в следующем. Областьальтернатив, заданная ограничениями (6.2), (6.3), (6.4), покрывается равномерно распределенными точками. В каждой точке вычисляютсязначения целевых функций, и результаты систематизируются в виде специальных таблиц, в которых критерии упорядочены. Такие таблицы называют таблицами испытаний(ТИ). Далее решение задачи сводится к анализу ТИ. Проектировщик (ЛПР) просматривает на дисплее независимо друг от друга ТИ каждого критерия, обращая внимание на следующие факты:

1) в каких пределах заключены показатели f_j( ) для каждого j;

2) как много точек f_j( ) отвечают «хорошим» проектным решениям;

3) каков «средний» уровень показателей в данной таблице и как сильно разбросаны вокруг него остальные решения.

В зависимости от ситуации проектировщик назначает2r чисел f_i ^* и f_i^**, i = 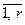, являющихся, соответственно, нижними и верхними границами, фигурирующими в тех неравенствах (6.4), которые образуют условия приемлемости проектного решения. После этого ПЭВМ в автоматическом режиме проверяет совместимость критериальных ограничений, т.е. определяет множество решений, одновременно удовлетворяющих ограничениям 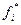≤ ≤ 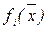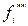, i = 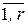. Если такие точки существуют, то это говорит о том, что задача имеет решение. Если нет, то можно ослабить критериальные ограничения или жеувеличить число точек в области поиска и после этого еще раз применить диалоговую процедуру определения границ. После конечного числа шагов получится допустимое множестворешений D, удовлетворяющее ограничениям (6.2), (6.3), (6.4).

Каким образом использовать полученные решения?

1). Во многих случаях проектировщик (ЛПР) предпочитает сам назначить «наилучшее» решение путем тщательного изучения полученного допустимого множестварешений. В этом случае есть возможность облегчить еще работу по изучению точек допустимого множества. Можно с помощью ЭВМ исключить заведомо «плохие» решения, т.е. выделить множество Парето G в множестве D. Таким образом, при поиске «наилучшего» решения ЛПР может ограничиться изучением множества G. Более того, множество G может быть использовано при назначении критериальных ограничений на каждом шаге диалоговой процедуры. После конечного числа шагов итерационной процедуры количество точек в множестве G можно сократить доминимума и тем самым облегчить принятие окончательного решения.

2) Другой способ использования множества D – это попытка сформулировать решающее правило, т.е. критерий, и искать его оптимум в допустимой области. При этом решения, полученные в результате осуществления описанной диалоговой процедуры, можно использовать в качестве начального приближения.

Данный подход можно успешно использовать тогда, когда отсутствуют явные выражения целевых функций и ограничений задачи.