Скорость витания, методы ее расчета, практическое значение.

При свободном падении твердой частицы в жидкой или газовой среде, находящейся в покое, только в первый момент наблюдается ускоренное движение; в дальнейшем возникающая сила сопротивления уравновешивается действием силы тяжести и частица падает равномерно, с постоянной скоростью. Эта скорость называется гидравлической крупностью. Это понятие имеет большое значение при изучении процессов взвешивания и отстаивания в жидкости, а также для расчета трубопроводов для гидротранспорта частиц.

При изучении аналогичных процессов в воздушной среде используется понятие скорости витания. Под последней понимают скорость восходящего потока воздуха (в вертикальной трубе), при которой твердые частицы, находящиеся в этом потоке, будут совершать колебательные движения приблизительно на одном уровне (как бы витать), т.е. будут находиться во взвешенном состоянии. Иначе говоря, это понятие эквивалентно гидравлической крупности применительно к воздушной среде.

Выведем формулу скорости витания частицы шарообразной формы.

Сила тяжести частицы (или её вес) 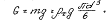где r_t - плотность частицы.

В воздушной среде частица падает под действием силы G¢, меньшей чем G, вследствие влияния архимедовой силы А. 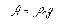где r0 - плотность воздуха.

Таким образом, сила падения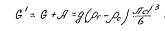

Сила сопротивления при падении частицы в воздухе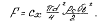

Так как эти силы уравновешиваются при равномерном падении, то 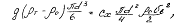откуда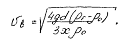

Поскольку плотность воздуха r0 значительно меньше плотности rт транспортируемого материала, разность rт-r0 без большой ошибки можно заменить на rт. Тогда формула для скорости витания шарообразной частицы принимает вид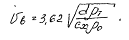

Итак, зная коэффициент сопротивления частицы cx, нетрудно по формуле определить скорость витания. Так как значения cx в свою очередь, зависят от скорости, задача решается методом подбора.

Для частиц определенной формы коэффициент лобового сопротивления зависит только от числа Рейнольдса, поэтому уравнение равномерного осаждения (всплывания) твердых частиц можно представить в виде зависимости числа Рейнольдса от критерия Архимеда: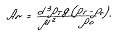

При Re<2 скорость витания определяется по уравнению Стокса: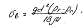

Для области действия закона Стокса (Ar<=36) используется зависимость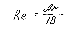

Для переходной области, где 2<Rе<500, что соответствует изменению критерия Ar в пределах 36<Ar<83000,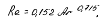

Для автомодельной области, где Ar>83000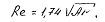

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

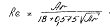
Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений, отвечающим этой области, значение Re и находят по нему скорость осаждения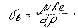

В практических условиях форма твердых частиц, концентрация и характер транспортируемого материала различны. Поэтому, чтобы получить конкретные данные для расчета, скорость витания различных материалов определяют экспериментальным путем в специальной трубе витания. Она изменяется в широких пределах - от 2 до 12 м/с.

Для обеспечения пневмотранспорта твердых материалов среднюю скорость движения воздуха в трубопроводе берут несколько большей (в зависимости от формы частиц и концентрации материала) скорости витания, определенной для шаровидной частицы по формуле (21).

Понятие скорости витания по существу относится к вертикальным участкам трубопроводов пневмотранспорта. На горизонтальных участках условия для перемещения твердых частиц иные.

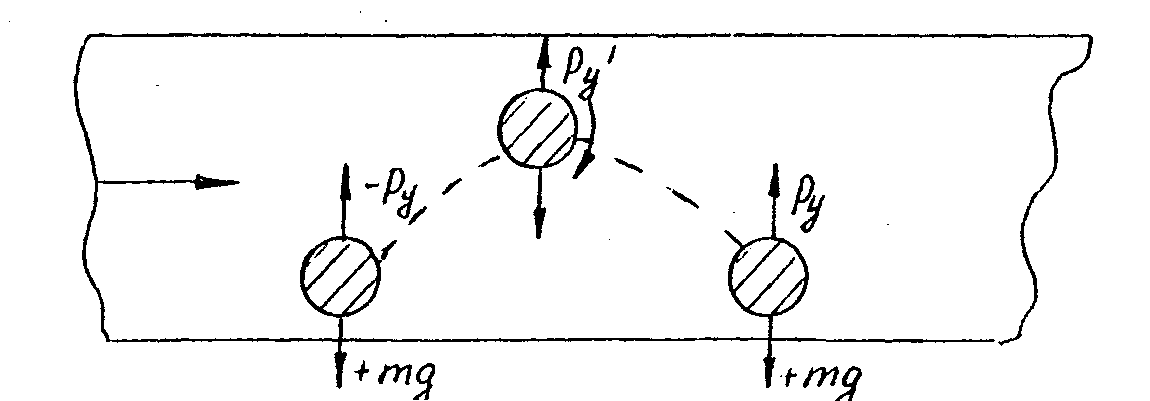
Рассмотрим механизм перемещения твердых частиц в горизонтальной трубе (рис.). Возьмем шаровидную частицу, расположенную на дне трубы. При обтекании шара, как и при обтекании цилиндра, вверху частицы вследствие увеличения скорости образуется область пониженного давления и возникает подъемная сила P, которая при достаточной скорости поднимает частицу. Сила сопротивления F перемещает частицу в направлении движения воздуха в трубе, а сама частица начинает вращаться (в данном случае по часовой стрелке) в результате эффекта вязкостного трения. В дальнейшем, когда частица поднялась, действие подъемной силы Р прекращается,| но вращение частицы благодаря инерции и наличию поперечного градиента осредненных скоростей сохраняется. Последнее образует циркуляцию и соответствующую ей подъемную силу Pу (эффект Магнуса). Эта сила, как правило, недостаточна для поддержания частицы во взвешенном состоянии. Поэтому частица, описав некоторую траекторию, падает на дно трубы и описанное явление повторяется.

В результате частицы движутся в воздушном потоке, описывая сложные, а после поворота, трубы - винтовые траектории. Средняя скорость потока воздуха, при которой частицы начинают двигаться указанным образом в горизонтальной трубе, называется скоростью веяния.

Если весьма увеличить скорость течения воздуха, то можно добиться того, что твердые частицы будут перемещаться в горизонтальном трубопроводе, не падая на дно, т.е. будут находиться во взвешенном состоянии. Такая способность турбулентного потока объясняется наличием в нем поперечных пульсаций. Однако осуществлять пневмотранспорт таким образом вследствие большой разницы плотностей воздуха и материала экономически нецелесообразно, а в некоторых случаях даже невозможно. Наоборот, гидротранспорт, где разность плотностей материала и воды в большинстве случаев незначительна, осуществляется при таких скоростях течения воды, когда частицы находятся во взвешенном состоянии.

Скорость веяния по абсолютной величине мало отличается от скорости витания. Поэтому на практике расчет пневмотранспорта ведут по скорости витания.

Рис. Механизм перемещения твердых частиц потоком воздуха в горизонтальном направлении