Микросостояние системы – это конкретное расположение отдельных частиц (молекул) в данный момент времени, которое соответствует наиболее устойчивому состоянию системы.

Итак, в качестве критерия возможности протекания процесса можно использовать W – термодинамическую вероятность. Она является функцией состояния и максимальна при равновесии. Однако W связана с механическими характеристиками системы: скорость молекул, их положение в пространстве и так далее. А для химической термодинамики важно найти критерий направления процесса, определяемый термодинамическими параметрами: Т, Р, V (температура, давление, объем).

Второе начало термодинамики вводит в рассмотрение новый критерий – энтропию, S, которая служит мерой энергетического беспорядка в системе. Энтропия связана с термодинамической вероятностью соотношением: S= klnW, где k=R/N_A » 1,381 ^. 10^-23 Дж/град – это константа Больцмана, имеет размерность энергии, отнесенной к температуре и одной частице. Следовательно, с ее помощью осуществляется переход от просто «беспорядка» системы к «энергетическому беспорядку». В расчете на 1 моль частиц: S= R lnW.

Изменение энтропии в процессе определяется изменением числа микросостояний системы DS = S₂ – S₁ = R ln W₂/W₁.

В учебниках для II-го начала термодинамики обычно приводится множество формулировок, например,

«Теплота не может самопроизвольно передаваться от более холодного тела к более горячему» (Клаузиус).

«Теплота наиболее холодного из участвующих в процессе тел не может служить источником работы» (Томсон).

«Коэффициент полезного действия паровой машины всегда меньше единицы» и т.д.

Но они, в большей степени, важны для физических процессов. А для химических процессов важно то, что второе начало термодинамики дает критерии того, какие процессы могут проходить самопроизвольно, а какие нет.

Опыт показывает, что многие самопроизвольно протекающиепроцессы идут с выделением теплоты (DН<0). Но среди самопроизвольных процессов встречаются также эндотермические (DН>0). Примером является растворение аммония нитрата в воде:

NH₄NO₃ (т) ® NH₄NO₃ (ж); DН⁰_х.р. = + 27 кДж/моль.

Получается, тепловыделение не является решающим критериемвозможности самопроизвольного протекания процессов.

Так же могут самопроизвольно протекать процессы с уменьшением энтропии (DS<0): С + О₂ ® СО_2.

Между молекулами углерода С и кислорода О₂ устанавливается связь, и поэтому степень энергетического беспорядка уменьшается.

Каков же критерий самопроизвольности – теплота или энтропия?

Критерием, определяющим возможность протекания процесса, есть баланс действия энтальпии (Н) и энтропии (S).Поэтому возможны самопроизвольные процессы с поглощением теплоты (если рост энергетического «беспорядка» является более весомым), и процессы с DS<0, (если это сопровождается более сильным выделением теплоты).

Измеряется изменение энтропии приведенной теплотой обратимого процесса, связывающего соответствующие состояния системы:

DS = Q_обр./Т.

Для необратимых процессов: DS >Q_необр./Т (алгебраическая сумма приведенных теплот для необратимых процессов: Q_{необр.проц.} < Q_{обр .проц.}

Математическая формулировка II закона термодинамики (обобщенная формула) выглядит следующими образом:

DS ³ Q/T

Для изолированных систем, где обмен энергией с окружающей средой исключен Q=0, неравенство, выражающее второе начало термодинамики примет вид: DS ³0.

Таким образом, для изолированных систем остается только один критерий самопроизвольного протекания процессов – увеличение энтропии. Самопроизвольными являются лишь процессы, ведущие к увеличению общей энтропии.Итак:

1.Энтропия – это функция состояния системы, поэтому вычислять изменение энтропии можно, используя следствие из закона Гесса. Энтропия химической реакции равна разности между суммами энтропий продуктов реакции и энтропий исходных веществ, с учетом стехиометрических коэффициентов.

DS_х.р. = S S_прод. - S S_исх.в-в, с учетом стехиометрических коэффициентов.

Задача: Рассчитать изменение энтропии химических реакций (DS_х.р.) для процесса: 3С₂Н₂ (г) ® С₆Н6 _(ж).

Решение: DS_х.р. = S⁰ (C₆H₆ (ж)) – 3 S⁰ (С₂Н₂ (г)).

DS_х.р. = 269,2 – 3 ^. 200,8 = - 333,2 Дж/моль.

2.Энтропия измеряется приведенной теплотой.

Задача: Чему равно приращение энтропии моля Fe при Т_пл=1536⁰С (1809 К) при переходе из кристаллического в жидкое состояние, если энтальпия DН_пл = 13765 Дж/моль.

При температуре плавления Fe_кр Û Fe_ж ( в равн. Þ T=const) = Т_пл.

ß

DS_пл = S (Fe (ж)) -S (Fe (т)) =DН_пл/Т_пл= 13765/1809= 7,61 Дж/К^. моль.

DS>0 Þ процесс при Т_пл протекает самопроизвольно.

3.Энтропия является критерием самопроизвольного протекания процессов только для изолированных систем. Самопроизвольно протекают в изолированных системах только те процессы, которые идут с увеличением энтропии.

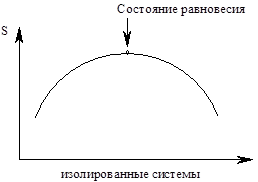
DS³0 DS³0

рис 9

4. S связана с числом возможных микросостояний в системе (, т.е. с термодинамической вероятностью,W), характеризует меру энергетического беспорядка. S= klnW в системе.

5. S – это термодинамическая функция, которая в отличие от термодинамической вероятности W связана с термодинамическими величинами Q; T, т.е. более приемлема для химической термодинамики.

Однако, в природных процессах и в технике чаще встречаются системы взаимодействующие с окружающей средой, т.е. неизолированные. Энтропия, S мало подходит для характеристики процессов в этих условиях.

Для изохороно-изотермических условий первый закон термодинамики имеет следующую математическую форму записи:

Q_V = DU (A= РDV; DV= const Þ A=0)

Из II –го закона термодинамики следует: DS ³ Q_V /T Þ Q_V £ ТDS.

Объединяя два выражения, получим: TDS ³ DU;DU - TDS £ 0.

Обозначим разность DU - TDS через новую термодинамическую функцию состояния – свободную энергию Гельмгольца, DU - TDS =DF.

Следовательно II-е начало термодинамики применительно к изохороно-изотермическим процессам можно записать так: DF£ 0.

Введение данной функции позволяет пользоваться лишь одним критерием направления процесса (какой для изолированных систем является S). Однако этот чисто формальный прием не отменяет того факта, что на самом деле для самопроизвольных процессов по прежнему остаются те же критерии: DН и DS. Через DF обозначен их баланс.

Итак: 1. для изохорно-изотермических условий DF является

суммарным критерием самопроизвольного протекания процессов

DF=DU - TDS (это выражение объединенных I и II законов термодинамики).

2.Самопроизвольными являются такие процессы для изохорно изотермических условий, в которых энергия Гельмгольца убывает

(DF< 0).

DF£ 0 DF£ 0

DF= 0

рис10

DF<0, процессы могут идти самопроизвольно; DF= 0, процессы занимают пограничное положение, характеризующееся минимальным значением;

DF > 0, процессы сами проходить не могут.

3.Энергия Гельмгольца является функцией состояния системы, поэтому вычислить изменение энергии Гельмгольца можно, используя следствие из закона Гесса.

Энергия Гельмгольца химической реакции равна разности между суммами энергий Гельмгольца продуктов реакции и энергий Гельмгольца исходных веществ, с учетом стехиометрических коэффициентов.

DF_х.р. = SDF⁰_прод. - SDF⁰_исх.в-в, с учетом стехиометрических коэффициентов.

Для изобарно-изотермических условийI-ый закон термодинамики можно записать в виде: Q_P = DU + РDV; т.е.теплота при изобарно-изотермических условиях равна изменению энтальпии Q_P = DU + pDV = DH (при условии, что не совершается никакой иной работы, как против давления). Объединяя неравенство D S ³ Q_P/T (выражение II закона термодинамики), получим вид: DН - ТDS £0. Если выражение DН - ТDS обозначить через новую термодинамическую функцию состояния – свободную энергию Гиббса, DG :

DН - ТDS = DG,

следовательно II –е начало термодинамики, применительно к изобарно-изотермическим процессам можно записать так: DG £0.G – энергия Гиббса, является также как и энергия Гельмгольца лишь балансом все тех же двух критериев самопроизвольного протекания процессов: выделения теплоты и возрастания энтропии. Итак,

1. для изобарно-изотермических условий DG является суммарным критерием самопроизвольного протекания процессов DG = DН - ТDS ( объединенный ( I и II ) закон термодинамики).

2.Процессы, в которых DG убывает (DG< 0) протекают самопроизвольно.

D G < 0, химические процессы могут идти самопроизвольно;

DG = 0, химические процессы занимают пограничное (равновесное) положение;

DG > 0, химические процессы сами проходить не могут.

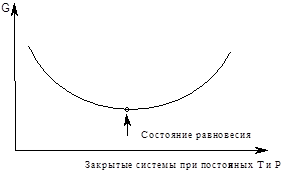DG £ 0 DG £ 0

DG = 0

рис.11

3. Энергия Гиббса DG является функцией состояния системы, поэтому вычислить изменение энергии Гиббса химических реакций можно по следствию из закона Гесса. Энергия Гиббса химических реакций равна разности между суммами энергий Гиббса продуктов реакции и энергий Гиббса исходных веществ, с учетом стехиометрических коэффициентов.

DG_х.р= SDG⁰_прод. - S DG⁰_{исх..в-в.}, с учетом стехиометрических коэффициентов.

DG⁰_обр. (Х) – стандартная энергия Гиббса вещества Х при стандартных условиях и в определенном агрегатном состоянии.

DG⁰_сг. (Х) – стандартная энергия сгорания вещества – это DG реакции окисления до конечных оксидов 1 моля Х. Для простых веществ и элементов DG⁰_обр.(Х) (как и DН⁰_обр.(Х)) равны нулю.

Задача: Спиртовое брожение происходит по уравнению реакции:

С₆Н₁₂О₆(ж) ® 2С₂Н₅(ОН)(ж) + 2СО₂(г)

DG⁰_обр, кДж/моль -915 -174 -394

Решение:

DG⁰_х.р. = 2(-174) + 2(-394) – (-915)= -221 кДж/моль

DН⁰_х.р. этого процесса составляет –79 кДж/моль. Следовательно, за счет энтропийного вклада способность брожения совершать полезную работу увеличивается почти втрое. Это очень важно, так как подобные процессы служат важнейшим источником энергии как у многих так называемых анаэробных организмов, так и у животных и человека при интенсивной мышечной нагрузке.

4. Функция G называется энергией, так как определяет работоспособность соответствующего процесса. А именно, DG численно рана полезной максимальной работе, которая могла бы быть совершена в ходе изобарно-изотермического процесса.