ДИНАМИЧЕСКИЙ РЕЖИМ СИСТЕМ.

Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины. Установившийся режим является не более чем частным случаем состояния системы на определенных временных интервалах ее работы. Процесс установления требуемого значения управляемой величины называется регулированием, и, ввиду инерционности звеньев регулирования, развивается во времени.

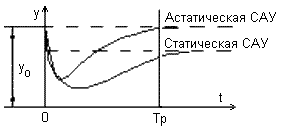
Рис. 2.3.1.

Динамическим называется режим работы системы, при котором входная и выходная величины системы изменяются во времени. Как правило, динамический режим возникает в результате перехода системы от одного установившегося состояния к другому, и поэтому его часто называют переходным режимом, а процесс перехода от одного установившегося состояния к другому - переходным процессом. Типичный пример переходных процессов для статических и астатических систем приведен на рис. 2.3.1.

Динамический режим, характеризующийся протеканием в ней определенных переходных процессов, является основным режимом работы систем. Зависимость выходной величины от изменяющейся во времени входной величины называют динамической характеристикой системы.

Все динамические характеристики можно разделить на две группы.

К первой группе относятся зависимости выходной величины системы от времени, если входная величина изменяется по типовому закону (импульсный, линейный и т.п.). Это так называемые временные характеристики.

Вторую группу динамических характеристик составляют частотные характеристики. К ним относятся зависимости выходной величины или ее параметров от частоты входной величины, изменяющейся по гармоническому закону.

Переходные процессы в системе. Зависимость выходной величины системы от времени, если входная величина изменилась на единый скачок, называют переходной характеристикой.

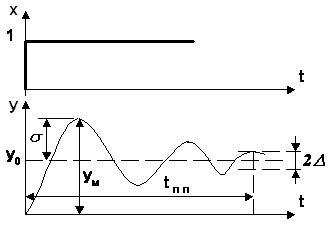
Рис. 2.3.2.

Допустим, система находится в установившемся режиме, и имеет значение выходной величины y = y₀. Пусть в момент t = 0 на объект воздействовал какой-либо управляющий или возмущающий фактор x(t), отклонив значение регулируемой величины от номинальной. Через некоторое время регулятор вернет систему к первоначальному состоянию (с учетом статистической ошибки). Если этот переходной процесс происходит по апериодическому временному закону (как на рис. 2.3.1), то процесс регулирования называется апериодическим. При резких возмущениях в системах возможен колебательный затухающий процесс (рис. 2.3.2), а в неустойчивых системах - возникновение незатухающих колебаний и расходящийся колебательный процесс.

Таким образом, переходная характеристика - это реакция элемента системы на ступенчатое изменение входной величины, как правило, единичное x(t) = 1(t). Под входной величиной понимается любой из управляющих или возмущающих воздействий, в многомерных или многоканальных системах – одно из воздействий. Переходная характеристика может быть задана таблично, графически или аналитически в виде системы уравнений {x = 1(t), y = F(t)}.

Оценки переходных характеристик производятся с помощью следующих показателей:

– Характер временной зависимости. По характеру зависимости переходные характеристики делятся на монотонные и колебательные. Переходная характеристика считается монотонной, если она имеет не более одного экстремума. В противном случае переходную характеристику относят к колебательной (немонотонной).

– Время переходного процесса – это время, в течение которого выходная величина после начала изменения входной достигает нового установившегося значения. Теоретически это время стремиться к бесконечности, поэтому за время переходного процесса принимают время, за которое выходная величина достигает нового установившегося значения с заданной степенью точности t_пп, обычно порядка 3-5% от нового установившегося значения. Нетрудно заметить (рис. 2.3.2). что степень точности D соответствует статической ошибке регулирования.

– Динамическая ошибка – это разность между действительным значением выходной величины y_i в данный момент (t_i) и её новым установившемся значением y₀, т.е.

Dy(t) = y(t) – y₀. (2.2.1)

Динамическая ошибка представляет собой функцию времени. Максимальную положительную относительную ошибку за время переходного процесса называют выбросом. Выброс определяется формулой (см. рис. 2.3.2):

s = (y_м – y₀) / y₀ (2.2.2)

– Колебательность - количество полных колебаний за время переходного процесса. Колебательность может характеризоваться частотой или периодом колебаний выходной величины.

Импульсная характеристика является другой не менее распространенной временной характеристикой системы. Её называют импульсной переходной характеристикой или функцией веса и обозначают h(t). Это зависимость выходной величины системы от времени, если входная величина изменилась на единичный идеальный импульс.

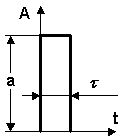
Рис. 2.3.3.

Для получения импульсной характеристики используют импульсы прямоугольной формы (рис. 2.3.3). Такой импульс аналитически определяется выражениями:

A(t) = 0, 0 > t > t;

A(t) = a, 0 ≤ t ≤ t;

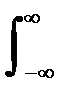A(t) dt = at.

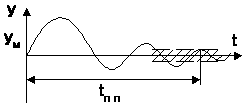
Рис. 2.3.4.

Произведение at часто называют величиной импульса. Если величина импульса равна единице, то импульс называют единичным. Если t → 0, то импульс называет идеальным. Он является теоретической дельта-функцией d(t) с бесконечной амплитудой в точке t=0 и площадью, равной 1.

Импульсная характеристика – это реакция системы на идеальное единичное импульсное изменение входной величины. Она может быть задана аналитически в виде системы уравнений {x = d(t), y = F(t)}. Так как идеальный импульс представляет собой производную скачка, d(t) = d 1(t) / dt, то импульсная характеристика есть производная переходной характеристики системы. Оценка импульсной характеристики производится теми же показателями, что и переходной. Пример характеристики приведен на рис. 2.3.4.