Непосредственное формирование матрицы узловых потенциалов

Выбор базисных переменных, т.е. переменных относительно которых строится математическая модель, позволяет минимизировать число уравнений математической модели. Так, в базисе узловых потенциалов закон Кирхгофа для напряжений удовлетворяется тождественно:

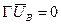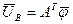, но , следовательно

.

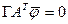Однако, 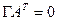, поэтому последнее уравнение выполняется при любых 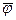. Таким образом, в топологической подсистеме остаются только уравнения, соответствующие закону Кирхгофа для токов. Таким образом, математическая модель цепи в базисе узловых потенциалов представляется системой уравнений вида:

,

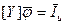где [Y] – матрица проводимостей цепи, 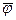- вектор узловых потенциалов, 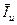- вектор токов, воздействующих на цепь.

Итак, рассмотрим формирование математической модели в базисе узловых потенциалов.

1. Рассмотрим линейную цепь, не содержащую зависимых источников, под воздействием генераторов тока:

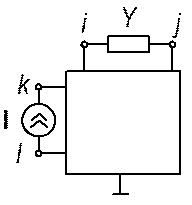
Составим [Y] – матрицу цепи согласно следующему алгоритму:

· Формируется главная диагональ матрицы. Элементы диагонали Y_ii равны суммам проводимостей элементов цепи, подключенных к i-ому узлу

· Формируются внедиагональные элементы матрицы. Внедиагональные элементы Y_ij равны суммам проводимостей элементов цепи, подключенных между i-ым и j-ым узлами, взятыми со знаком минус.

Для изображенной на рисунке цепи имеем:

i j

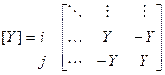
[Y] – матрица пассивной цепи обладает следующими свойствами:

· Матрица симметрична относительно главной диагонали

· Сумма элементов столбцов матрицы равна сумме проводимостей элементов, подключенных между земляным узлом и узлом с номером, равным номеру столбца.

Таким образом, при составлении матрицы достаточно заполнить диагональ и один из треугольников матрицы (верхний или нижний). Второе свойство целесообразно использовать для проверки правильности формирования матрицы.

После формирования Y – матрицы, формируется вектор правой части 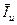. Элементы вектора соответствуют токам генераторов, воздействующих на цепь. Если ток втекает в узел, элементу присваивается знак «+», иначе «–». Так, для изображенной на рисунке цепи:

.

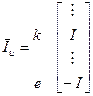2. Рассмотрим цепь, под воздействием генераторов напряжения.

В этом случае для формирования вектора правой части необходимо осуществить преобразование генератора напряжения в генератор тока. Для этого используется внутреннее сопротивление генератора. Тогда, по теореме об эквивалентном генераторе:

В более общем случае выполняются преобразования вида:

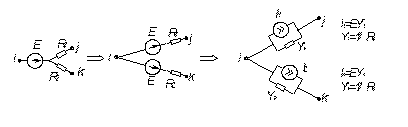
3. Рассмотрим активную цепь, или цепь, содержащую управляемые генераторы (источники). Согласно принятой классификации, управляемые источники подразделяют на 4 типа:

· Источники напряжения, управляемые напряжением (ИНУН):

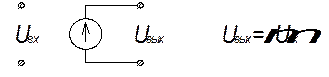
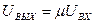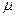, где - коэффициент усиления по напряжению.

К данному типу относятся усилители напряжения.

· Источники напряжения, управляемые током (ИНУТ):

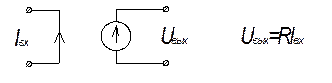
К данному типу относятся так называемые трансимпедансные усилители.

· Источники тока, управляемые током (ИТУТ):

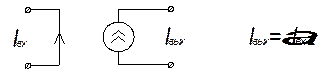
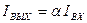, где - коэффициент усиления по току.

К данному типу относятся усилители тока.

· Источники тока, управляемые напряжением (ИТУН):

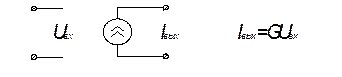
К данному типу относятся так называемые транскондуктивные усилители.

Как видно из приведенных соотношений необходимой размерностью – проводимость – обладает лишь параметр ИТУН. Только параметр зависимого источника данного типа может быть непосредственно внесен в [Y] – матрицу цепи. Включение параметра осуществляется по следующему правилу:

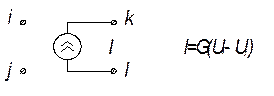
i j

.

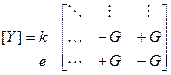Источники иных типов должны быть преобразованы к виду ИТУН. Для этого используются входные и выходные импедансы источников. Преобразование осуществляется по теореме об эквивалентном генераторе:

· ИНУН:

.

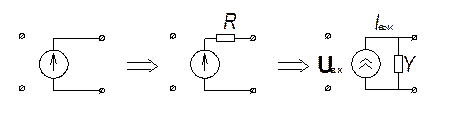
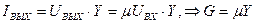· ИНУТ:

.

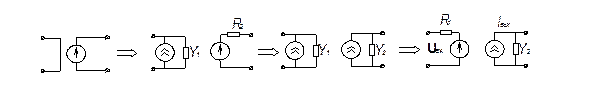
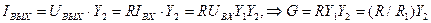· ИТУТ:

.

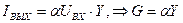Пример:

Рассмотрим активный ФНЧ:

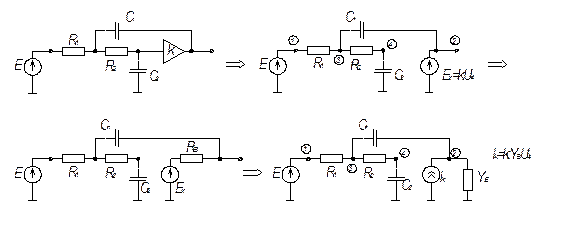
Математическая модель в матричной форме в базисе узловых потенциалов:

.

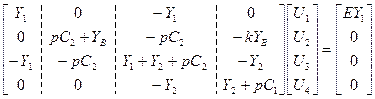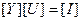
4.2.2. Алгоритм автоматизированного формирования математической модели в базисе узловых потенциалов

Рассмотрим алгоритм формирования математической модели для цепей различного вида.

1. Линейная, пассивная цепь.

Выделим обобщенную k-ую ветвь цепи, содержащую линейный импеданс, генераторы тока и напряжения.

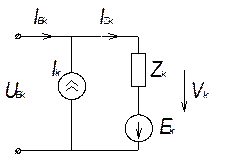
Введем в рассмотрение следующие вектора токов и напряжений:

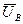– вектор падений напряжений на ветвях цепи,

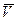– вектор падений напряжений на импедансах,

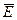– вектор внешних воздействий,

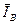– вектор токов ветвей цепи,

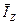– вектор токов импедансов,

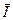– вектор внешних воздействий.

, , ,

, , .

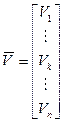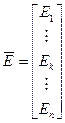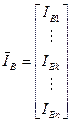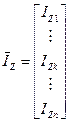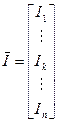Для k-ой ветви выполняются следующие соотношения:

, .

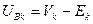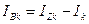Обобщая, в матричной форме получим:

,

.

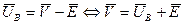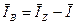Согласно закону Кирхгофа для токов, с помощью матрицы инциденций запишем:

.

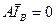После подстановки :

.

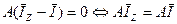Введем в рассмотрение компонентную матрицу 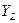вида:

.

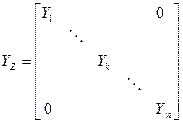Тогда:

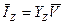
Подставив это выражение в соотношение для 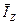, представим:

,

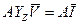или

,

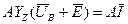поскольку

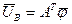, где 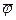- вектор узловых потенциалов, то:

,

.

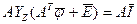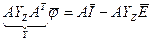Окончательно:

,

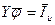где Y – матрица проводимостей цепи,

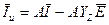– вектор токов внешних воздействий, причем слагаемое 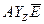соответствует преобразованию генераторов напряжения в генераторы тока.