Определение статистических характеристик ОЭП измерения
КПД ОЭП
КПД ОЭП ηоэп определяет, какая доля оптического сигнала, поступившего на вход прибора (т.е. на его входной зрачок), используется для создания выходного сигнала, несущего полезную информацию.
Смысл этого коэффициента не ограничивается одними потерями сигнала. Он должен учитывать все возможные факторы снижения отношения сигнал/шум μ в ОЭП. Поэтому он должен учитывать два аспекта:
- потери оптического сигнала при прохождении оптической системы и регистрации на приемнике излучения (ПИ);
- возможное возрастание шумов.
В общем случае КПД ОЭП определяют следующим образом:
1. 
учитывает: потери излучения в оптической системе:
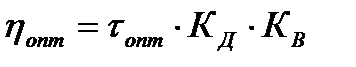
τопт – учитывает традиционные потери в оптической системе. Они известны. Это - отражение на границе оптических сред (Френелевские потери), поглощение в оптических средах, потери излучения при зеркальном отражении.
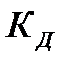- потери на диафрагмирование;
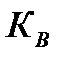- потери на виньетирование.
Общее выражение для τопт хорошо известно:
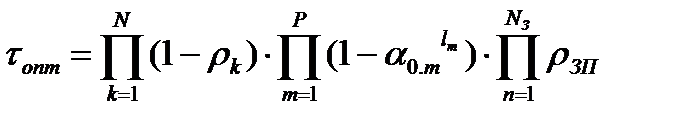
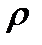- коэффициент отражения от границ сред (прозрачных поверхностей);
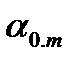- коэффициент поглощения на единицу пути в оптической среде;
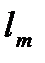- путь в оптической среде;
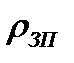- коэффициент отражения от зеркальных поверхностей.
ВОПРОСЫ:
5.1. Чему равен (примерно, цифра, которая необходима нам для быстрой оценки возможных потерь) коэффициент отражения ρ от непросветленной оптической поверхности, с показателем преломления n=1,5…1,6? Какие потери ожидаются в оптической системе, состоящей из 12 непросветленных поверхностей?
5.2. А от оптической поверхности, просветленной в широком спектральном диапазоне (например, в видимом диапазоне спектра)?
5.3. А от оптической поверхности, просветленной для одной длине волны (например, на длине волны работы лазера)?
5.4. Чему равен ρзп для оптического зеркала с покрытием из Al?
– Какие потери ожидаются в оптической системе, состоящей из 5 зеркал с покрытием из Al?
Вывод.
Эти потери незначительны для оптических систем, состоящих из 1 – 2 оптических элементов. Например, объектив из одной двухлинзовой склейки.
Но наша задача при проведении расчета энергетических параметров оптического сигнала - не потерять порядок. С другой стороны - разработка, скажем, приемной оптической систем, у которой τопт =0,1 вызывает недоумение.
Поэтому для многокомпонентной системы расчет τопт – очень важная задача!
2. 
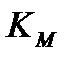отражает потери при модуляции и обработке модулированного сигнала.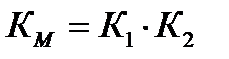 
Коэффициент К1 учитывает непосредственные потери в результате модуляции:
,
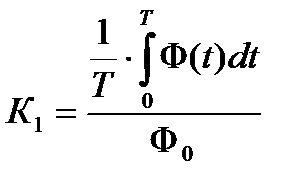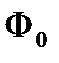- поток на входе модулятора;
- закон модуляции.
Т – период модуляции
ВОПРОС:
5.5. Чему равен К1 для синусоидальной (гармонической) модуляции ? Это значительный уровень потерь?
Второй коэффициент сложнее по своей сути. Его расчет не так очевиден.
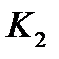- коэффициент, учитывающий тот факт, что в следующих за приемником излучения звеньях может обрабатываться только некоторая часть спектр модулированного сигнала.
|
|
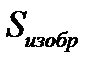
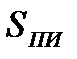
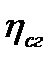учитывает, что параметры приемника излучения могут быть не согласованы как с оптическим, так и с электронным трактом.
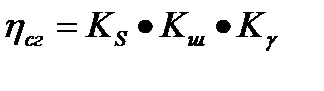
Первый коэффициент Кs – площадной. Он учитывает тот факт (редко встречающийся на практике), что в некоторых случаях площадь пятна рассеяния излучения, сформированного приемной оптической системой в плоскости приемника излучения – Sизобр может превосходить по размером площадь фотоприемника Sпи :
.
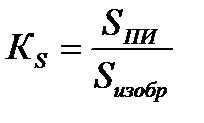В этом случае потери полезного сигнала очевидны.
Следующий коэффициент учитывает уже шумы.
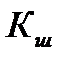- коэффициент шума, приведенный к выходу ПИ. Он учитывает тот факт, что кроме шумов приемника σшПИ излучения присутствуют шумы электронного тракта σшЭ, приведенные к выходу приемника излучения
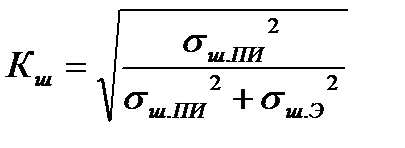
И, наконец, еще один коэффициент Кν учитывает тот факт, что уровень шума на частоте паспортизации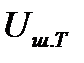 
и уровень шума на рабочей частоте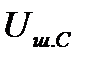 
могут отличаться. В этом случае:
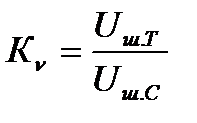
Определение статистических характеристик ОЭП измерения
К статистическим характеристикам ОЭП относятся
- вероятность правильного обнаружения – Робн ;
- вероятность ложной тревоги - Рлт;
- вероятность правильного необнаружения - Рпр необн;
- вероятность пропуска объекта -Рпроп.
Как определяются эти характеристики?
Какие исходные данные надо знать, чтобы определить статистические характеристики ОЭП?
Для того, чтобы ответить на эти вопросы рассмотрим работу ОЭП измерения при обнаружении сигнала.
Или, другими словами – рассмотрим процедуру обнаружения сигнала при наличии внешних шумов.
Что присутствует в поле зрения ОЭП? В поле зрения ОЭП присутствуют – источник полезного сигнала, источник шумов. Во входной зрачок поступает смесь сигнала и шума.
Итак, мы рассматриваем сигнал, шум и смесь (сигнала и шума).
Чтобы ввести статистические характеристики, на первом этапе необходимо исследовать статистику распределения сигнала и шумов (установить их мат. ожидание, дисперсию, распределение плотности вероятности случайной функции, описывающей сигнал, шум или смесь);
ВОПРОС:
5.6. Интересно, можем ли мы с помощью нашего ОЭП экспериментально исследовать:
- статистику распределения сигнала?
- статистику распределения шума?
- статистику распределения смеси?
Как осуществить эти эксперименты?
Охарактеризуем случайную величину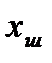 
ее математическим ожиданием 
и дисперсией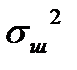 
. Введем систему обозначений:
| Мат. ожидание | Дисперсия | Распределение плотности вероятности | |
| Шум |
|
| 
|
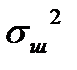
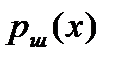
| Сигнал | 
| 
| 
|
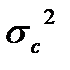
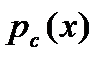
| Смесь (сигнал + шум) | 
| 
| 
|
;
.
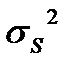
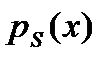
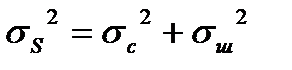Если объекта в поле зрения ОЭП измерения нет, то сигнал на выходе электронного блока ОЭП будет определяться статистикой сигнала от подстилающей поверхности или естественных и организованных помех. Этому случаю соответствует следующее распределение плотности вероятности случайной функции, описывающей шум – Рш(х).
Если объект присутствует в поле зрения ОЭП – то этому случаю соответствует распределение плотности вероятности смеси РS(х). Эти два события поясняются рис.
В ОЭП принимается решение, есть объект в поле зрения или нет, по некоторым критериям; простейшим критерием является превышение значением смеси сигнала и шума порогового значения 
.
-пороговое значение сигнала.
Пороговый уровень может быть задан постоянным, а может – изменяющимся по заранее обусловленной программе, например, в зависимости от зарегистрированного сигнала, шума (смеси).
ВОПРОС;
5.7. На рисунке х0 показан в точке пересечения Рш(х) и РS(х). Это получилось случайно, или в этом есть закономерность?
Итак, простейшая задача обнаружения сводится к тому, что ОЭП должен дать правильный ответ – есть ли в угловом поле обзора объект, или его нет?
Эти два случая принято называть правильным обнаружением и правильным необнаружением.
Двумя другими, альтернативными случаями являются «ложная тревога», когда полезного сигнала нет, но уровень помех превышает и «пропуск сигнала», когда объект находится в поле зрения, но смесь не превышает .
В таком случае выражения для определения статистических характеристик ОЭП становятся понятными:
Вероятность правильного обнаружения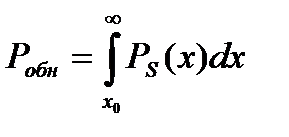 
;
вероятность ложной тревоги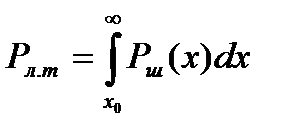 
;
вероятность пропуска цели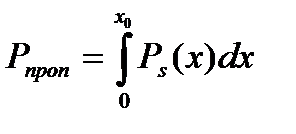 
;
вероятность правильного необнаружения 
.
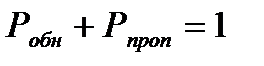
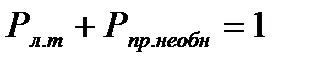
ВОПРОС
5.7. Чему равняется сумма двух статистических характеристик: Робн + Рлт ?
Суммы каких статистических характеристик равны единице?
Теперь понятно, что для определения статистических характеристик надо знать статистику распределения шума и смеси.
А после этого необходимо назначить пороговое значение 
. Это тоже отдельный вопрос.
Кажется, все просто: чем меньше , тем больше вероятность правильного Робн обнаружения, следовательно, важнейшая статистическая характеристика растет!
Но обратим внимание – при этом растет и вероятность ложной тревоги Рлт. Не менее важная статистическая характеристика!
Поэтому назначение осуществляется по некоторым критериям, устанавливающим связь между статистическими характеристиками.
Известен целый ряд критериев. Например - критерий Котельникова (критерий идеального наблюдателя): минимизируется сумма значений вероятности ложной тревоги и пропуска цели.
Или: критерий Неймана-Пирсона: одна из ошибочных функций назначается, вторая – минимизируется.
По сути дела, решается оптимизационная расчетная задача.
А что происходит с вероятностью правильного обнаружения – Робн и с вероятностью правильного необнаружения - Рпр необн? Какие значения можно достигнуть при назначении х0 по этим критериям? Ответ, увы, такой – каких достигли при оптимизации, таких и достигли!!
Конечно, исследовать и определить статистику распределения сигнала и шума, или провести цикл оптимизационных расчетов и назначить значение х0 - это достаточно трудоемкие задачи, связанные и с программированием и с проведением численных расчетов.
Хотя, в некоторых случаях, когда можно аппроксимировать функции распределений шума и смеси известными функциями, задачу можно решить аналитически.
Ниже приведен пример такого случая, когда статистика смеси и шума описываются распределение Гаусса: (этот пример приводится без подробных пояснений – предлагается разобраться самим!!)
,
.
. 
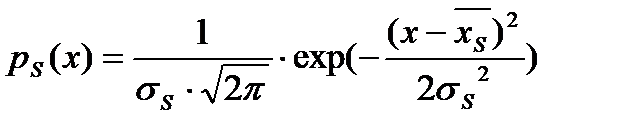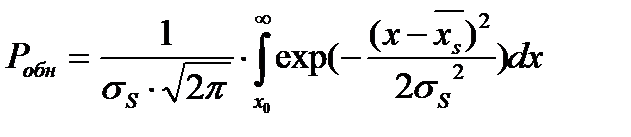
Введем: 
, 
, 
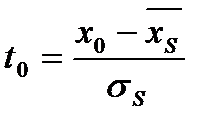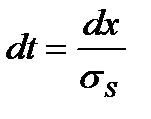. Тогда
.
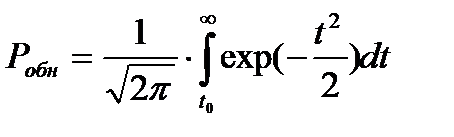Интеграл вероятности 
.
Его свойства – Ф(x) =1 при x стремящемся к бесконечности
И Ф(x) = Ф(-x) – четная функция
.
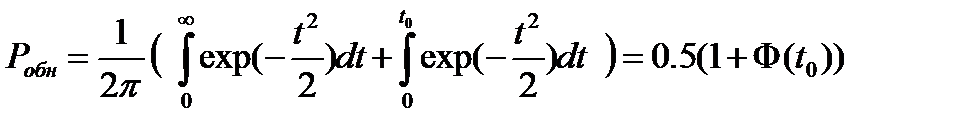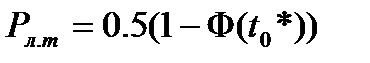, где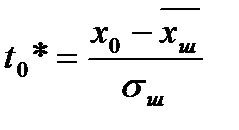 
.
Дата добавления: 2020-04-12; просмотров: 500;
Поиск по сайту
Узнать еще
- I. Общая характеристика категории состояния как часть речи
- I. Определение и структура методов обучения.
- I. Определение условий выполнения рукописи.
- I. Определение, виды радиоактивности, радиоактивные семейства
- II. Виды ионизирующих излучений и единицы измерения ИИ
- II. Лексико-грамматические разряды имен числительных. Их характеристика.
- II. Лексико-грамматические разряды местоимений. Их общая характеристика
- II. Основные характеристики микроскопа.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
