Энергия частиц и температура газа
Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.
Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.
Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:
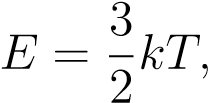 (2)
(2)
где k = 1,38 · 10−23 Дж/К — постоянная Больцмана.
Из данной формулы можно получить выражение для средней квадратической скорости частиц. Подставим (1) в (2):
откуда 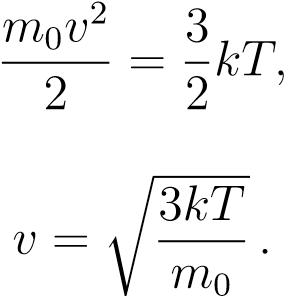
В эту формулу входит масса частицы m0, которую ещё надо вычислить. Но можно получить более удобный вариант формулы, домножив числитель и знаменатель подкоренного выражения на число Авогадро NA:
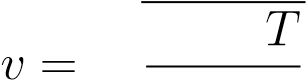 r3kNA
r3kNA
.
m0NA
В знаменателе имеем: m0NA = µ — молярная масса газа. В числителе стоит произведение двух констант, которое также является константой:
Дж Дж
−23 23 −1
R = kNA= 1,38 · 10 · 6,02 · 10 моль = 8,31 .
К моль· К
Константа R называется универсальной газовой постоянной.
Теперь формула для средней квадратической скорости приобретает вид:
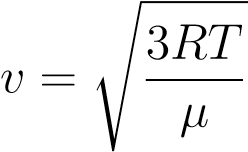 .
.
Такое выражение гораздо более удобно для практических вычислений.
Решение задач
Задача №1
При какой температуре средняя кинетическая энергия поступательного движения молекул газа равна 6,21*10-21 Дж?
Дано: Решение:
Ек=6,21*10-21 Дж Eк= 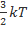 =>
=> 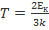 =
= 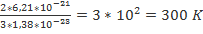
Т-? Ответ:300 K
Задача №2
При какой температуре средняя квадратичная скорость молекул азота 830 м/с?
Дано: Решение:
V=830м/с V= 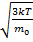 => T=
=> T= 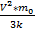
Т-? m0= 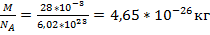
Т= 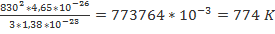
Ответ:774 K
Задача №3
Какова средняя квадратичная скорость молекул кислорода при температуре 300К?
Дано: Решение:
Т=300К V= 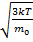
Vср-? m0= 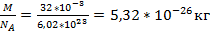
V= 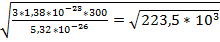 =473м/с
=473м/с
Ответ: 473м/с
Дата добавления: 2020-04-12; просмотров: 878;











