Анализ опыта Майкельсона – Морли
Российский ученый В.А. Ацюковский скрупулезно проанализировал экспериментальные основы эйнштейновских теорий относительности и пришел к такому выводу: "Анализ результатов экспериментов, проведенных различными исследователями в целях проверки положений СТО и ОТО, показал, что экспериментов, в которых получены положительные и однозначно интерпретируемые результаты, подтверждающие положения и выводы теорий относительности А. Эйнштейна, не существует".
Это заключение распространяется и на самый знаменитый опыт – опыт Майкельсона-Морли. Обратите внимание, интерферометр Майкельсона-Морли был неподвижен относительно Земли, двигался только свет. Авторы полагали, что им удастся зафиксировать влияние скорости движения Земли V = 30км/с относительно Солнца на отклонение интерференционной полосы света. Расчет производился по формуле
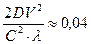 . (422)
. (422)
Ожидаемое смещение 0,04 интерференционной полосы не было зафиксировано. И авторы почему-то не стали искать причину расхождений между теорией и экспериментом. Давайте сделаем это за них.
Так как фотоны имеют массу, то Земля для них – инерциальная система отсчёта и их поведение в поле силы её тяжести не должно отличаться от поведения в этом поле других тел, имеющих массу, поэтому мы обязаны подставить в вышеприведенную формулу не скорость движения Земли относительно Солнца (V = 30 км/с), а скорость поверхности Земли (V = 0,5 км/c), формируемую ее вращением относительно своей оси. Тогда ожидаемое смещение интерференционной полосы в опыте Майкельсона-Морли составит не 0,04, а значительно меньше
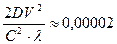 . (423)
. (423)
Неудивительно поэтому, что прибор Майкельсона-Морли показывал отсутствие смещения интерференционной полосы. И мы теперь знаем причину этого: у него не хватало необходимой чувствительности (точности).
Тем не менее, Нобелевский комитет выдал в 1907 г. А. Майкельсону Нобелевскую премию «За создание прецизионных оптических инструментов и выполнение с их помощью спектроскопических и метрологических исследований». Добавим, что ошибочная интерпретация эксперимента Майкельсона явилась экспериментальной базой ошибочных теорий относительности А. Эйнштейна.
А что если поставить такой опыт, чтобы в нем источник света и прибор, фиксирующий смещение интерференционной полосы, перемещались (вращались) бы в поле тяготения Земли? В этом случае сравниваются показания приборов при отсутствии вращения всей установки и при ее вращении. Сразу видно, что при отсутствии вращения установки принцип измерений не будет отличаться от принципа измерений в опыте Майкельсона-Морли и прибор не покажет никакого смещения интерференционной полосы. Но как только установка начнет вращаться в поле силы тяжести Земли, так сразу должно появиться смещение указанной полосы. Объясняется это тем, что пока свет идет от источника к приемнику, положение последнего меняется в поле силы тяжести Земли относительно источника, и прибор должен зафиксировать смещение указанной полосы.
Подчеркнем еще раз: положение источника и приемника сигналов в опыте Майкельсона-Морли не меняется друг относительно друга в поле силы тяжести Земли, а в описанном нами примере - меняется. Это главное отличие указанных опытов. Описанная элементарная логика убедительно подтверждена опытом Саньяка. Результаты его опыта противоречат показаниям интерферометра Майкельсона-Морли и этот факт релятивисты замалчивают и упорно игнорируют, ярко демонстрируя этим, что научная истина их не интересует.
Мы привели достаточно веские доказательства ошибочности эйнштейновских теорий относительности, поэтому невольно возникает вопрос: а как же теперь воспринимать тот факт, что теории относительности А. Эйнштейна лежат в фундаменте, как считают релятивисты, всех достижений физики в XX веке? Очень просто! Все эти достижения - результат усилий главным образом физиков-экспериментаторов, которые проводили эксперименты не с целью проверки физических теорий, а с целью получения такого результата, который бы можно было использовать в военных целях или в конкурентной борьбе при завоевании рынков сбыта своей продукции.
Теоретики, конечно, пытались найти объяснение этим достижениям, как-то их обосновать, но эти объяснения оказались приближенными и поверхностными. Главным тормозом в объяснении глубинных основ материи и мироздания был стереотип мышления, сформированный ошибочными теориями Эйнштейна, и настойчивость его сторонников в защите этих теорий от критики.
12.5. Как родились планеты Солнечной системы
Проанализируем лишь ту гипотезу о формировании планет Солнечной системы, согласно которой они образовались из звезды, пролетавшей вблизи Солнца, которое захватило её своим гравитационным полем (рис. 228, а).
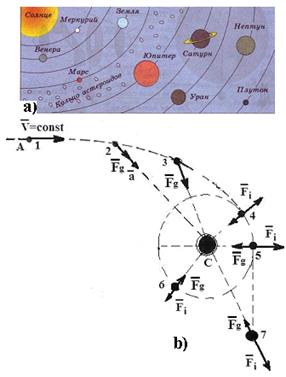
Рис. 228. a) - схема движения планет вокруг Солнца; схема
вовлечения звезды А гравитационной силой 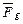 Солнца (С)
Солнца (С)
в орбитальное движение
Эта гипотеза позволяет найти ответы на большую часть главных вопросов, связанных с рождением планет.
Анализ процесса рождения планет Солнечной системы начнём с формулировки главных вопросов, ответы на которые должны следовать из этого анализа.
1. Почему орбиты всех планет почти круговые?
2. Почему орбиты всех планет лежат почти в одной плоскости?
3. Почему все планеты вращаются вокруг Солнца в одном и том же направлении?
4. Почему направления вращения планет (за исключением Урана) вокруг своих осей совпадают с направлениями их вращения вокруг Солнца?
5. Почему плоскости орбит большинства спутников планет близки к их экваториальным плоскостям?
6. Почему орбиты большинства спутников почти круговые?
7. Почему большинство спутников и кольцо Сатурна обращаются вокруг своих планет в том же направлении, что и планеты вокруг Солнца?
8. Почему существует градиент плотности планет?
9. Можно ли предполагать, что закономерность изменяющейся плотности планет, по мере удаления их от Солнца, аналогична изменению плотности существующего Солнца, начиная от его ядра до её поверхности?
10. Почему с удалением планет от Солнца их плотности вначале уменьшаются, а потом незначительно увеличиваются?
Мы уже показали, что формированием основных элементарных частиц: фотонов, электронов, протонов и нейтронов управляет закон сохранения кинетического момента (момента импульса), математической моделью которого является константа Планка (219). Мы назвали этот закон главным законом, управляющим формированием материального мира. Из этого следует, что этот же закон должен был управлять процессом рождения планет Солнечной системы. Сейчас мы убедимся в большой вероятности связи этой гипотезы с реальностью.
Поскольку планеты не имеют прямолинейных движений, а вращаются относительно Солнца и относительно своих осей, то для описания этих вращений мы будем пользоваться математической моделью закона сохранения кинетического момента 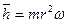 .
.
А теперь формулируем гипотезу. Планеты Солнечной системы сформировались из звезды 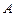 , пролетавшей мимо Солнца
, пролетавшей мимо Солнца 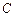 и захваченной её гравитационным полем (рис. 228, b, позиции: 1, 2, 3, 4, 5…). Когда звезда была далека от Солнца, то, двигаясь в пространстве, она вращалась только относительно своей оси, которая была параллельна (в основном) оси вращения Солнца. Вполне естественно, что звезда обладала собственным кинетическим моментом, величина которого нам не известна. Однако нам известно, что отсутствие внешних сил оставляло этот момент постоянным. По мере приближения к Солнцу на звезду начинала действовать сила гравитации
и захваченной её гравитационным полем (рис. 228, b, позиции: 1, 2, 3, 4, 5…). Когда звезда была далека от Солнца, то, двигаясь в пространстве, она вращалась только относительно своей оси, которая была параллельна (в основном) оси вращения Солнца. Вполне естественно, что звезда обладала собственным кинетическим моментом, величина которого нам не известна. Однако нам известно, что отсутствие внешних сил оставляло этот момент постоянным. По мере приближения к Солнцу на звезду начинала действовать сила гравитации 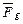 Солнца.
Солнца.
Предположим, что эта звезда пролетала мимо Солнца на расстоянии равном расстоянию от Солнца до самой первой планеты Меркурий. Вполне естественно, что сила гравитации Солнца 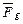 (рис. 228, b, позиции: 2, 3, 4…) вовлекла эту звезду в круговое движение вокруг Солнца. Следующее предположение заключается в том, что направление вращения звезды вокруг своей оси совпадало с направлением вращения звезды вокруг Солнца. В результате к кинетическому моменту вращения звезды относительно своей оси добавился кинетической момент вращения вокруг Солнца.
(рис. 228, b, позиции: 2, 3, 4…) вовлекла эту звезду в круговое движение вокруг Солнца. Следующее предположение заключается в том, что направление вращения звезды вокруг своей оси совпадало с направлением вращения звезды вокруг Солнца. В результате к кинетическому моменту вращения звезды относительно своей оси добавился кинетической момент вращения вокруг Солнца.
Поскольку звезда была в плазменном состоянии, как и Солнце, только меньше Солнца по массе и размеру, то она смогла бы удержаться на орбите только при условии равенства между центробежной силой инерции и силой гравитации 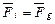 Солнца (рис. 228, b, позиция 5). Если этого равенства не было, то на образовавшейся первой орбите могла удержаться лишь та часть прочно связанной плазмы звезды (рис. 228, позиция 6), которая обеспечивала равенство между центробежной силой инерции и силой гравитации
Солнца (рис. 228, b, позиция 5). Если этого равенства не было, то на образовавшейся первой орбите могла удержаться лишь та часть прочно связанной плазмы звезды (рис. 228, позиция 6), которая обеспечивала равенство между центробежной силой инерции и силой гравитации 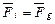 Солнца. Оставшаяся часть плазмы звезды начинала удаляться от Солнца под действием большей центробежной силы инерции
Солнца. Оставшаяся часть плазмы звезды начинала удаляться от Солнца под действием большей центробежной силы инерции 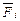 (рис. 228, позиция 7). В процессе удаления от Солнца из удаляющейся части звезды начинала формироваться следующая порция устойчивой структуры, которую гравитационная сила Солнца вновь выделила из плазмы звезды и образовала вторую планету – Венеру. Последовательность описанных событий и сформировала планеты вокруг Солнца.
(рис. 228, позиция 7). В процессе удаления от Солнца из удаляющейся части звезды начинала формироваться следующая порция устойчивой структуры, которую гравитационная сила Солнца вновь выделила из плазмы звезды и образовала вторую планету – Венеру. Последовательность описанных событий и сформировала планеты вокруг Солнца.
Теперь надо доказать достоверность описанного гипотетического сценария рождения Солнечной системы. Для этого соберём информацию о современном состоянии планет Солнечной системы. В эту информацию, необходимо включить массы всех планет и их больших спутников, плотности всех планет, их радиусы, а также радиусы орбит, орбитальные скорости, и угловые скорости вращения планет относительно своих осей. Эта информация позволит нам найти орбитальный кинетический момент звезды в момент начала её вращения вокруг Солнца. Звезда, удаляющаяся от Солнца за счёт того, что центробежная сила инерции больше силы гравитации 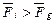 Солнца, будет оставлять на орбитах существующих планет столько плазменной массы, сколько они сейчас имеют её в твёрдом состоянии вместе со своими спутниками.
Солнца, будет оставлять на орбитах существующих планет столько плазменной массы, сколько они сейчас имеют её в твёрдом состоянии вместе со своими спутниками.
Вполне естественно, что суммарный кинетический момент всех современных планет будет равен кинетическому моменту звезды в момент начала её орбитального движения вокруг Солнца (рис. 228, b, позиция 5).
Итак, приведём основную информацию о Солнце и её планетах. Солнце имеет массу 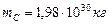 . Её радиус равен
. Её радиус равен 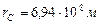 , а плотность
, а плотность 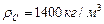 . Угловая скорость вращения Солнца относительно своей оси равна
. Угловая скорость вращения Солнца относительно своей оси равна 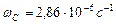 . Известно, что сумма масс всех планет и их спутников почти в 1000 раз меньше массы Солнца. Ниже, в табл. 61 приводятся массы планет Солнечной системы и их плотности.
. Известно, что сумма масс всех планет и их спутников почти в 1000 раз меньше массы Солнца. Ниже, в табл. 61 приводятся массы планет Солнечной системы и их плотности.
Таблица 61. Массы планет и их спутников, и плотности планет
| Планеты | Массы, 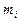 , кг , кг
| Плотности, 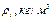
|
| 1. Меркурий | 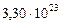
| |
| 2.Венера | 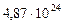
| |
| 3. Земля | 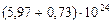
| |
| 4. Марс | 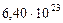
| |
| 5. Юпитер | 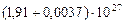
| |
| 6. Сатурн | 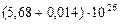
| |
| 7. Уран | 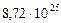
| |
| 8. Нептун | 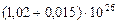
| |
| 9. Плутон | 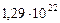
| |
| Итого | 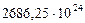
| 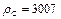
|
Основную информацию о параметрах планет мы брали в Интернете: Астрономия + Астрономия для любителей + Солнечная система + наименования планет + планета в цифрах. Оказалось, что составители этой справочной информации допустили ряд ошибок. Например, согласно их данным, радиусы орбит у Юпитера и Сатурна одинаковые, а у Нептуна радиус орбиты, выраженный в астрономических единицах, отличается от его величины, выраженной в километрах. Нам представляется, что публикуемая гипотеза заинтересует астрономов - профессионалов и они, владея более точной информацией, уточнят результаты наших расчётов.
Обратим внимание на последовательность изменения плотности 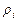 планет. Те из них, что ближе расположены к Солнцу, имеют большую плотность. По мере удаления планет от Солнца их плотность вначале уменьшается, а потом вновь растёт. Самая маленькая плотность
планет. Те из них, что ближе расположены к Солнцу, имеют большую плотность. По мере удаления планет от Солнца их плотность вначале уменьшается, а потом вновь растёт. Самая маленькая плотность 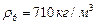 у Сатурна, а самая большая – у Земли. Удивительным является то, что Солнце, находясь в плазменном состоянии, имеет плотность (
у Сатурна, а самая большая – у Земли. Удивительным является то, что Солнце, находясь в плазменном состоянии, имеет плотность ( 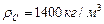 ) большую, чем у Юпитера, Сатурна и Урана, пребывающих в твёрдом состоянии.
) большую, чем у Юпитера, Сатурна и Урана, пребывающих в твёрдом состоянии.
Считается, что Сатурн состоит в основном из твёрдого водорода и гелия. В составе Нептуна и Плутона кроме водорода и гелия есть и другие химические элементы.
Если предположить, что все планеты образовались из звезды, то она должна была иметь градиент плотности, примерно, такой, какой сформировался у последовательно образовавшихся планет. Ядро звезды состояло из более тяжёлых химических элементов, которые рождались в процессе её жизни и эволюции и опускались её силами гравитации к центру. Тот факт, что Сатурн, имея самую низкую плотность, состоит в основном из водорода, провоцирует предположение о том, что водород, как главный источник термоядерных реакций, занимал среднюю область звезды, в которой и происходят термоядерные взрывы. Большая часть тяжёлых химических элементов, которые рождаются при этом, устремляется силой гравитации звезды к её ядру, а меньшая часть выбрасывается взрывами в направлении к поверхности звезды.
Описанное провоцирует нас также предположить, что современное Солнце тоже имеет градиент плотности с последовательностью, которую имеет градиент плотности последовательности планет (табл. 40). Из этого следует, что термоядерные реакции протекают, примерно, в средней сферической области Солнца, а протуберанцы на её поверхности - следствия этих взрывов.
Если описанная гипотеза изменения плотности звезды, пребывающей в плазменном состоянии, близка к реальности, то разность между центробежной силой и силой гравитации Солнца, действовавшая на пролетающую мимо звезду, должна была задержать, прежде всего, ту часть её плазмы, которая имеет наибольшую плотность, а значит наиболее прочную связь между молекулами химических элементов. Более легкая часть плазмы, с меньшей связью между молекулами химических элементов, должна быть удалена от Солнца центробежной силой инерции, большей чем гравитационная сила Солнца. Вероятность такого сценария подтверждают приливы и отливы в океанах Земли, формируемые гравитационной силой Луны, эквивалентной по действию силе инерции.
Конечно, вода - это не плазма, но её текучесть оказывается достаточной, чтобы реагировать на изменение величины силы гравитации Луны при изменении расстояния между поверхностью океана и Луной всего на 3,3%.
Радиусы планет и радиусы их орбит, а также угловые скорости вращения планет относительно своих осей и относительно Солнца и орбитальные скорости планет. Они представлены в таблицах 62, 63.
Таблица 62. Радиусы планет и радиусы их орбит
| Планеты | Радиусы планет, 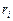 , м , м
| Радиусы орбит, 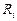 , м , м
|
| 1. Меркурий | 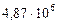
| 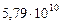
|
| 2. Венера | 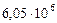
| 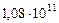
|
| 3. Земля | 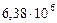
| 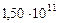
|
| 4. Марс | 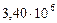
| 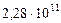
|
| 5. Юпитер | 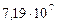
| 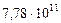
|
| 6. Сатурн | 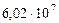
| 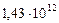
|
| 7. Уран | 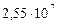
| 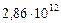
|
| 8. Нептун | 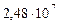
| 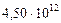
|
| 9. Плутон | 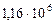
| 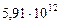
|
Орбитальные центробежные силы инерции 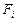 и гравитационные силы Солнца
и гравитационные силы Солнца 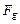 , действующие на современные планеты, представлены в табл. 64. Их равенство – доказательство устойчивости орбит (табл. 64).
, действующие на современные планеты, представлены в табл. 64. Их равенство – доказательство устойчивости орбит (табл. 64).
Таблица 64. Скорости планет
| Планеты | Собственные угло- вые скорости,
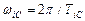 , рад/с , рад/с
| Орбитальные
угловые скорости,
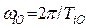 , рад/с , рад/с
| Орбитальные
скорости,
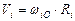 , м/с , м/с
|
| 1.Меркурий | 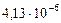
| 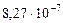
| 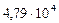
|
| 2. Венера | 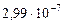
| 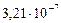
| 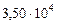
|
| 3. Земля | 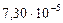
| 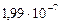
| 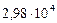
|
| 4. Марс | 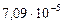
| 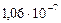
| 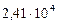
|
| 5. Юпитер | 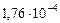
| 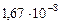
| 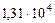
|
| 6. Сатурн | 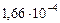
| 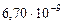
| 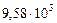
|
| 7. Уран | 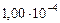
| 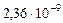
| 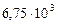
|
| 8. Нептун | 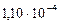
| 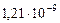
| 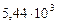
|
| 9. Плутон | 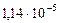
| 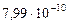
| 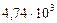
|
Вполне естественно, что на первой орбите, которую начинала формировать звезда, пришедшая из космоса к Солнцу, осталась лишь та часть её плазмы, которая обеспечила равенство между силой гравитации Солнца и центробежной силой инерции (табл. 65). Очевидно также и то, что такое разделение плазмы звезды начиналось в самом начале её вращения относительно Солнца, поэтому у плазмы, оставшейся на первой орбите, орбитальная скорость могла уменьшиться.
Таблица 65. Центробежные силы инерции и гравитационные силы
современных планет
| Планеты | 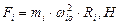
| 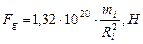
|
| 1. Меркурий | 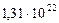
| 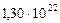
|
| 2. Венера | 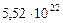
| 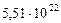
|
| 3. Земля | 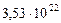
| 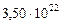
|
| 4. Марс | 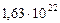
| 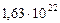
|
| 5. Юпитер | 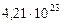
| 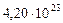
|
| 6. Сатурн | 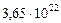
| 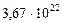
|
| 7. Уран | 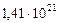
| 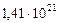
|
| 8. Нептун | 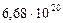
| 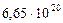
|
| 9. Плутон | 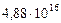
| 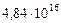
|
Естественно также, что силы гравитации той части плазмы, которая осталась на первой орбите, сформировали из неё сферическое образование, подобное форме современной планеты Меркурий (рис. 228, b, позиция 6).
Таким образом, на первой орбите осталось сферическое образование с достаточно большой плотностью, а оставшаяся часть плазмы звезды удалилась от Солнца центробежной силой инерции. В результате из удалявшейся плазмы силы гравитации сформировали вторую порцию плазмы с массой, обеспечивающей равенство между силой гравитации Солнца и силой инерции. Из этой порции образовалась вторая планета - Венера, а оставшаяся плазма бывшей звезды продолжила удаление от Солнца. Из неё потом и образовалась наша планета, а от удаляющейся части остатка звезды отделился ещё один объект, который мы теперь называем Луна. Так постепенно из плазмы бывшей звезды выделились порции с большей плотностью.
Настал момент, когда отделилась часть сферы с максимальным количеством водорода, обеспечивавшим термоядерные реакции звезды, и образовался вначале Юпитер, а потом Сатурн.
У оставшейся плазмы было меньше водорода и больше более тяжёлых химических элементов, которые были выброшены ядерными взрывами на поверхность звезды в период её нормальной активности. В результате, у самых дальних планет плотность увеличилась.
Конечно, процесс отделения каждой порции плазмы звезды очень сложен. Тут действуют силы связи между молекулами химических элементов и их кластерами, внутренние силы гравитации звезды, центробежные силы инерции вращения звезды относительно своей оси, орбитальные центробежные силы инерции и силы гравитации Солнца. Однако, плазменное состояние вещества звезды приводит к тому, что гравитационная сила Солнца задерживает на орбите, прежде всего, ту её часть, которая имеет наибольшую плотность, так как силы, объединяющие эту часть, больше сил, которые действуют в менее плотных слоях звезды. У удаляющейся части звезды силы гравитации вновь сформируют ядро из тех химических элементов, которые оказались ближе к её центру.
Из описанной схемы формирования планет мы сразу получаем ответ на вопрос о причинах движения их в одной плоскости и совпадения их вращений (исключая Уран) относительно своих осей и относительно Солнца с направлением вращения Солнца относительно своей оси.
Вполне естественно, что формирование спутников планет - следствие плазменного состояния частей звезды, удалявшихся от Солнца. Некоторые из этих частей отделялись от той части плазмы звезды, которая, выделив из себя порцию для формирования планеты, удаляясь от Солнца, потеряла ещё некоторую часть своей плазмы. Тот факт, что плотность Луны меньше плотности Земли подтверждает это предположение.
Что касается обратного вращения Урана относительно своей оси, то причин этого может быть несколько и их надо анализировать.
Итак, описанный процесс образования планет возможен, если на каждую орбиту будет приходить порция плазмы звезды, центробежная сила которой будет больше силы гравитации Солнца. Как это проверить?
Мы уже отметили, роль закона сохранения кинетического момента. Прежде всего, суммарная величина масс всех планет и их спутников должна быть равна массе звезды, из которой они образовались. Далее, суммарная величина кинетических моментов всех существующих планет и их спутников должна быть равна кинетическому моменту звезды в момент начала её вращения относительно Солнца (рис. 228, b, позиция 5). Обе эти величины легко рассчитываются. Результаты этих расчётов представлены в таблицах 65-66. Нам остаётся лишь дать пояснения по методике этих расчётов.
Таблица 65. Кинетические моменты современных планет
| Планеты | Собственные кинет.
моменты,
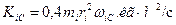
| Орбитальные кинет. моменты,
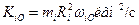
|
| 1. Меркурий | 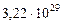
| 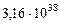
|
| 2. Венера | 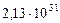
| 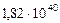
|
| 3. Земля | 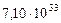
| 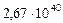
|
| 4. Марс | 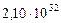
| 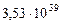
|
| 5. Юпитер | 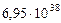
| 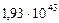
|
| 6. Сатурн | 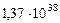
| 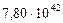
|
| 7. Уран | 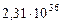
| 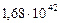
|
| 8. Нептун | 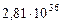
| 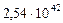
|
| 9. Плутон | 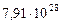
| 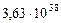
|
Информация, представленная в табл. 40, получена из справочных данных о планетах Солнечной системы. Величины угловых скоростей вращения планет вокруг собственных осей 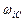 и вокруг Солнца
и вокруг Солнца 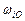 (табл. 63), необходимые для вычисления кинетических моментов вращения планет относительно своих осей и относительно Солнца, взяты из Интернета.
(табл. 63), необходимые для вычисления кинетических моментов вращения планет относительно своих осей и относительно Солнца, взяты из Интернета.
Таблица 66. Кинетические моменты современных планет
| Планеты | Орбитальные кинет.
моменты,
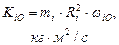
| Общие кинет. моменты,
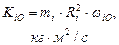
|
| 1. Меркурий | 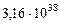
| 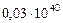
|
| 2. Венера | 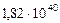
| 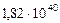
|
| 3. Земля | 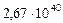
| 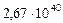
|
| 4. Марс | 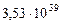
| 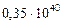
|
| 5. Юпитер | 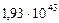
| 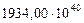
|
| 6. Сатурн | 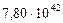
| 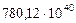
|
| 7. Уран | 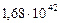
| 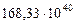
|
| 8. Нептун | 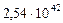
| 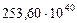
|
| 9. Плутон | 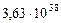
| 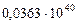
|
| Итого | 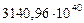
|
Обратим внимание на то, что планеты имеют формы, близкие к шаровым, поэтому их моменты инерции относительно своих осей вращения определяются по формуле 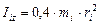 . Следующая важная информация (табл. 65): орбитальные кинетические моменты
. Следующая важная информация (табл. 65): орбитальные кинетические моменты 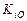 всех планет на несколько порядков больше кинетических моментов
всех планет на несколько порядков больше кинетических моментов 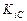 вращения их относительно своих осей. В результате для приближённых расчётов достаточно взять суммарные кинетические моменты всех планет, равные их орбитальным значениям.
вращения их относительно своих осей. В результате для приближённых расчётов достаточно взять суммарные кинетические моменты всех планет, равные их орбитальным значениям.
В таблице 65 представлены кинетические моменты вращения существующих планет относительно своих осей 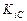 и орбитальные кинетические моменты
и орбитальные кинетические моменты 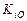 .
.
Конечно, при более точных расчётах суммарный кинетический момент 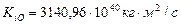 (табл. 66) всех планет может иметь другое значение, но в любом случае оно будет больше приведённой величины и это, как мы увидим дальше, увеличит разность между центробежными силами, действующими на звезду, из которой формируются планеты, и силой гравитации Солнца.
(табл. 66) всех планет может иметь другое значение, но в любом случае оно будет больше приведённой величины и это, как мы увидим дальше, увеличит разность между центробежными силами, действующими на звезду, из которой формируются планеты, и силой гравитации Солнца.
При этом надо учесть, что мы использовали в расчётах величины радиусов орбит существующих планет. Есть все основания полагать, что за миллионы лет радиусы этих орбит могли только уменьшиться. Поэтому реальнее будет увеличить величины радиусов существующих орбит в расчетах, но на сколько, мы пока не знаем. Увеличение радиусов орбит приведёт к увеличению центробежных сил, действовавших на первозданные планеты и уменьшению сил гравитации Солнца. В результате эффект разделения плазмы звезды на части с разной плотностью усилится.
Чтобы облегчить процесс сравнения кинетических моментов вращения планет относительно своих осей и относительно Солнца, представим их величины в одном порядке (табл. 66, вторая колонка).
Итак, звезда с массой 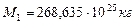 , равной массе всех существующих планет и их спутников (табл. 61), приближалась к Солнцу по касательной (рис. 228, b, позиции 1, 2) в плоскости её вращения на расстоянии
, равной массе всех существующих планет и их спутников (табл. 61), приближалась к Солнцу по касательной (рис. 228, b, позиции 1, 2) в плоскости её вращения на расстоянии 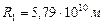 (табл. 62), равном радиусу орбиты современного Меркурия (рис. 228, b, позиция 2). Сила гравитации Солнца захватила её и она начала вращаться вокруг Солнца с начальным кинетическим моментом
(табл. 62), равном радиусу орбиты современного Меркурия (рис. 228, b, позиция 2). Сила гравитации Солнца захватила её и она начала вращаться вокруг Солнца с начальным кинетическим моментом 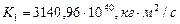 (табл. 66). Зная массу звезды
(табл. 66). Зная массу звезды 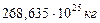 , можем определить начальную угловую скорость её вращения относительно Солнца
, можем определить начальную угловую скорость её вращения относительно Солнца 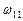 из соотношения (397).
из соотношения (397).
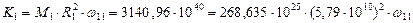 .(424)
.(424)
Отсюда
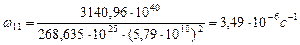 . (425)
. (425)
Теперь определим массы первозданных планет, которые последовательно отрывались центробежной силой инерции, удаляясь от Солнца (табл. 67).
Примечание. Под понятием «первозданные планеты» мы понимаем их плазменное состояние в момент прихода на орбиту перед процессом отделения от общей массы плазмы звезды той её части, которая останется на орбите и сформирует саму планету на этой орбите (табл. 67).
Таблица 67. Массы 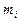 современных и
современных и 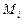 первозданных планет
первозданных планет
| Планеты | Массы современных планет и их спутников, 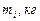
| Массы первозданных планет и их спутников, 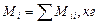
|
| 1. Меркурий | 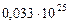
| 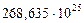
|
| 2. Венера | 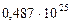
| 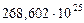
|
| 3. Земля | 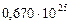
| 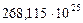
|
| 4. Марс | 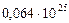
| 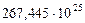
|
| 5. Юпитер | 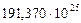
| 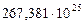
|
| 6. Сатурн | 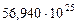
| 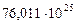
|
| 7. Уран | 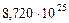
| 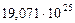
|
| 8. Нептун | 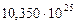
| 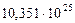
|
| 9. Плутон | 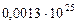
| 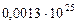
|
| Итого | 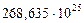
|
Тогда кинетические моменты первозданных планет и их начальные орбитальные угловые скорости были такими, какие представлены в табл. 68.
Обратим внимание на то, что мы направили звезду по существующей орбите Меркурия и её общий кинетический момент, равный общему кинетическому моменту современных планет 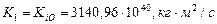 , позволяет определить начальную орбитальную угловую скорость звезды
, позволяет определить начальную орбитальную угловую скорость звезды 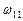 (425). В результате центробежная сила инерции, действовавшая на звезду – первозданный Меркурий, была равна
(425). В результате центробежная сила инерции, действовавшая на звезду – первозданный Меркурий, была равна
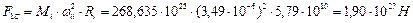 .(426)
.(426)
Силу гравитации, действующую на планету, можно представить в таком виде
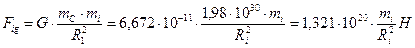 (427)
(427)
Таблица 68. Кинетические моменты и орбитальные угловые скорости первозданных планет
| Планеты | Кинет. моменты
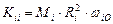
| Орбит. угловые скорости 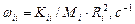
|
| 1. Меркурий | 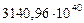
| 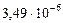
|
| 2. Венера | 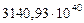
|  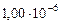
|
| 3. Земля | 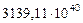
|  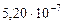
|
| 4. Марс | 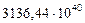
| 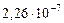
|
| 5. Юпитер | 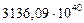
| 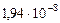
|
| 6. Сатурн | 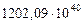
| 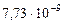
|
| 7. Уран | 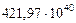
| 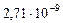
|
| 8. Нептун | 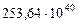
| 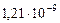
|
| 9. Плутон | 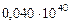
| 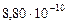
|
Тогда гравитационная сила Солнца, действовавшая на звезду – первозданный Меркурий, была равна
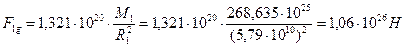 .(428)
.(428)
Как видно, центробежная сила инерции 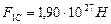 (426),действовавшая на звезду – первозданный Меркурий (рис. 228, b, позиция 5) была больше гравитационной силы Солнца
(426),действовавшая на звезду – первозданный Меркурий (рис. 228, b, позиция 5) была больше гравитационной силы Солнца 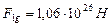 (427) почти на порядок. Вполне естественное, что плазменное состояние Звезды сразу же привело к её расслоению за счёт дисбаланса между центробежной силой инерции и силой гравитации Солнца.
(427) почти на порядок. Вполне естественное, что плазменное состояние Звезды сразу же привело к её расслоению за счёт дисбаланса между центробежной силой инерции и силой гравитации Солнца.
Наибольший кинетический момент 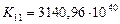 имел первозданный Меркурий (табл. 68) - звезда, которая, в момент начала вращения вокруг Солнца, расслоилась и наиболее плотная её часть, связанная воедино химическими связями молекул и гравитационными силами, продолжала движение по орбите (рис. 228, b, позиции 6), а оставшуюся часть плазмы сила инерции начала удалять от Солнца (рис. 228, b, позиция 7, табл. 69).
имел первозданный Меркурий (табл. 68) - звезда, которая, в момент начала вращения вокруг Солнца, расслоилась и наиболее плотная её часть, связанная воедино химическими связями молекул и гравитационными силами, продолжала движение по орбите (рис. 228, b, позиции 6), а оставшуюся часть плазмы сила инерции начала удалять от Солнца (рис. 228, b, позиция 7, табл. 69).
Результаты табл. 69 убедительно показывают, что на всех орбитах современных планет, в момент прихода к ним звезды, из которой они рождались, центробежная сила инерции была больше силы гравитации Солнца.
Таблица 69. Центробежные силы инерции и гравитационные силы первозданных планет
| Планеты | Дата добавления: 2016-06-22; просмотров: 3053; |











