Физика колебательного контура

конденсатор + индуктивность

Конденсатор и индуктивность – основные элементы колебательных систем. Схематически они показываются просто (рис. 137, a).

Считается, что одна пластина конденсатора С заряжена отрицательно, а другая положительно. Если конденсатор электролитический, то это соответствует реальности, так как указанные потенциалы формируют кластеры ионов, на одном конце которых отрицательно заряженный электрон, а на другом - положительно заряженный протон (рис. 135, 136, a). Другое дело - провод, по которому движутся электроны. В нём не могут присутствовать одновременно и электроны, и протоны, так как их соседство заканчивается образованием атомов водорода и плазмы с температурой до 10000 С.

Таким образом, процессы, протекающие в конденсаторах и индуктивностях, а также в проводах, которые соединяют их, остаются скрытыми для понимания.

Давно известно, что однократное включение питания схемы конденсатор – индуктивность (рис. 137, а) приводит к появлению затухающих синусоидальных колебаний напряжения (рис. 137, b). Чтобы понять что происходит в этот момент в схеме конденсатор – индуктивность, представим конденсатор и катушку индуктивности в виде полутора витков и покажем направления движения электронов 1 и 2 в витках катушки при разрядке конденсатора (рис. 137, с). Одновременно попытаемся найти ответ на главный вопрос электрофотонодинамики: в чём сущность причины, формирующей колебательный процесс изменения напряжения в системе конденсатор – индуктивность (рис. 137, c)?

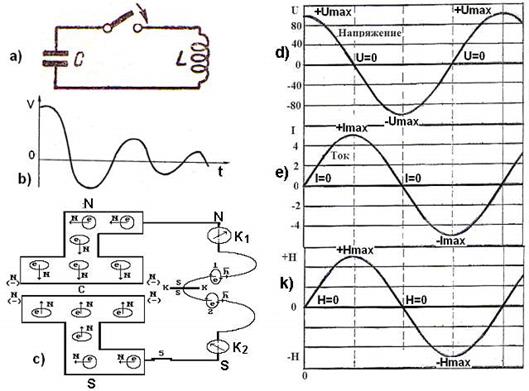
Рис. 137: а) схема конденсатор + индуктивность;

b) график затухающей синусоиды;

с) схема процессов движения электронов в цепи:

конденсатор – индуктивность при разрядке конденсатора;

d), e) и k) закономерность изменения напряжения, тока и

напряжённости магнитного поля при разрядке конденсатора

на катушку индуктивности (рис. 137, c)

Чтобы найти ответ на поставленный вопрос, проследим за движением электронов к катушке индуктивности. Главное в этом процессе – направления движения электронов из конденсатора в катушку индуктивности. Мы уже показали, что эта задача решается вполне удовлетворительно с помощью древнейшего прибора – компаса. Установим эти компасы ( и ) на провода, подходящие от конденсатора к катушке индуктивности, предварительно сориентировав их в направлении с юга на север (рис. 137, c).

Итак, проследим за движением электронов от конденсатора к катушке индуктивности вблизи клемм этой катушки. Обратим внимание на отличия в ориентации электронов в проводах, соединяющих конденсатор и катушку индуктивности (рис. 137, с), зафиксированные отклонением стрелок компасов ( и ).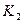

Теперь видно (рис. 137, с), что электроны от верхней и нижней пластин конденсатора встречаются в середине катушки индуктивности (сечение К-К) одноимёнными зарядами и одноимёнными южными магнитными полюсами. Это автоматически формирует процесс их отталкивания друг от друга, и они устремляются вновь к пластинам конденсатора.

Когда конденсатор заряжен, то напряжение на его пластинах в момент включения выключателя 5 максимально и равно, например, 100 В (рис. 137, d).

Совокупность магнитных полей всех электронов во всех витках катушки формирует суммарное магнитное поле, направление силовых линий, которого легко определяется по направлению спинов 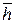электронов 1 и 2 (рис. 137, c). Эти электроны подходят к сечению К-К с противоположно направленными векторами спинов и магнитных моментов. Это значит, что сформированные ими магнитные поля вокруг витков катушки, в зоне встречи электронов (сечение К-К) направлены навстречу друг другу одноимёнными магнитными полюсами (рис. 137, с) и тоже отталкиваются. Когда электроны, идущие от верхней и нижней пластин конденсатора С, встретятся в сечении К-К катушки, то конденсатор C полностью разрядится.

Итак, к моменту начала разрядки конденсатора, напряжение U на его клеммах имеет максимальное значение (рис. 137, b, 137, d; +Umax), ток I и напряжённость H магнитного поля катушки, равны нулю (рис. 137, e и k; I=0, H=0). В момент прихода электронов к сечению К-К катушки и их остановки, напряжение на клеммах конденсатора оказывается равным нулю (рис. 137, d; U=0), а величины тока и напряженности магнитного поля катушки – максимуму (рис. 137, e и k; +Imax, +Hmax).

Далее, напряжённость магнитного поля катушки начинает уменьшаться (рис. 137, e) и автоматически изменяет направление векторов спинов и магнитных моментов электронов на противоположное, и они, двигаясь назад к конденсатору, формируют на его клеммах противоположную магнитную полярность. В момент прихода электронов к пластинам конденсатора, отрицательное напряжение на его клеммах достигает максимального отрицательного значения (рис. 137, d; -Umax), а величины обратно направленных тока и напряженности магнитного поля принимают нулевые значения (рис. 137, e и k; I=0, H=0).

После этого начинается второе движение электронов от пластин конденсатора к катушке. При этом электроны меняют направления векторов магнитных моментов и спинов на противоположные. В результате величина противоположного (отрицательного) потенциала на пластинах конденсатора начинает уменьшаться до нуля (рис. 137, d; U=0), а величина тока, обусловленная движением электронов с противоположно направленными векторами спинов, увеличиваясь, уходит в отрицательную зону (рис. 137, e; -Imax). Так же изменяется и напряженность противоположно направленного магнитного поля катушки (рис. 137, k; -Hmax). Так формируется синусоидальный процесс изменения напряжения, тока и напряжённости магнитного поля вокруг проводов катушки. Если после первого замыкания и размыкания электрической цепи в схеме: конденсатор – индуктивность (рис. 137, а) этот процесс не повторится, то амплитуда напряжения начнёт уменьшаться, а процесс его колебаний - затухать (рис. 137, b).

Обратим внимание на то, что перезарядку конденсатора осуществляет один носитель электрического заряда – свободный электрон, без участия положительно заряженного протона, который не существует в проводах в свободном состоянии. Поэтому у нас нет никакого права приписывать пластинам конденсатора разную электрическую полярность. Они получают разную магнитную полярность.

Итак, у нас появилась возможность составить уравнения изменения напряжения U, тока I и напряжённости Н магнитного поля в колебательном контуре конденсатор – катушка индуктивности. Поскольку в момент начала разрядки конденсатора напряжение U на его клеммах максимально, ток I и напряжённость магнитного поля Н минимальны, то уравнения их изменения запишутся так:

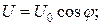(295)

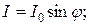(296)

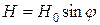. (297)

Это и есть исходные уравнения, заменяющие уравнения Максвелла при описании процессов, протекающих в колебательном контуре конденсатор + индуктивность.

Заключение

Специалистам понятно, что при отсутствии информации о структуре электрона невозможно описать процесс работы колебательного контура: конденсатор - индуктивность. Этот процесс раскрывает свои экспериментальные тайны (рис. 137, d, e и k) при анализе поведения в нём, выявленной и глубоко обоснованной нами модели электрона (рис. 42, а).