Связь задач извлечения квадратных корней и факторизации по модулю RSA. Криптосистема Рабина.

Пусть дано сравнение x²≡a(mod pq), p, q – различные большие простые числа. Как следует из предыдущего пункта, решение данного сравнения можно найти, решив систему 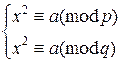, при этом необходимым условием существования решения является 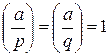. В том случае, если решения существуют, исходное сравнение имеет четыре различных решения: x≡±x₁(mod pq), x≡±x₂(mod pq)

Утверждение.

Для модуля RSA (n=pq, p, q – различные большие простые числа) задачи факторизации и извлечения квадратных корней вычислительно эквивалентны.

(Напомним, что две проблемы называются вычислительно эквивалентными, если за полиномиальное время по решению одной из них находится решение другой и наоборот.)

Доказательство:

1) Действительно, если умеем факторизовать модуль, то сможем извлечь квадратные корни по этому модулю (разложив исходное сравнение в систему и решив ее за полиномиальное время).

2) Если же разложения модуля RSA на простые сомножители неизвестно, но известны 4 различных решения сравнения x²≡a(mod n), и эти решения суть ±x(mod n), ±y(mod n). Выберем пару чисел x, y. Заметим, что x²≡y²(mod pq), x 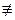±y(mod pq).

x²≡y²(mod pq) 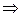x²—y² =(x+y)(x—y)≡0 (mod pq), причем x+y 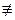0(mod pq),

x—y 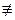0(mod pq). То есть pq\(x+y)(x—y), но pq не делит x+y, pq не делит x—y. Пользуясь основным свойствам простых чисел а также в силу равноправия сомножителей p и q, заключаем, что p\(x+y), q\(x—y), и тогда

p=НОД(x+y, n)

q=НОД(x—y, n).

Вычисление наибольшего общего делителя осуществляется при помощи полиномиального алгоритма – алгоритма Евклида.

□