Производная неявной функции
8.1. Функция одной переменной. Пусть 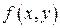 – функция двух переменных. Рассмотрим уравнение
– функция двух переменных. Рассмотрим уравнение
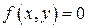 . (1)
. (1)
Предположим, что при каждом допустимом значении 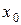 уравнение (1) имеет единственное решение
уравнение (1) имеет единственное решение 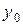 . Это означает, что уравнение (1) задает неявную функцию
. Это означает, что уравнение (1) задает неявную функцию 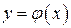 , и, значит, для этой функции уравнение (1) превращается в тождество:
, и, значит, для этой функции уравнение (1) превращается в тождество:
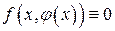 .
.
Пример 8.1. Дано уравнение
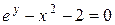 .
.
Из этого уравнения найти неявную функцию 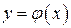 .
.
Решение. Ясно, что при каждом 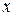 это уравнение имеет по
это уравнение имеет по 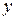 единственное решение, определяемое формулой
единственное решение, определяемое формулой
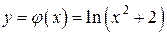 .
.
Проверим выполнение тождества:
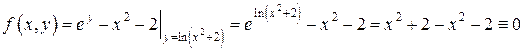 .
.
Следовательно, данное уравнение определяет единственную неявную функцию 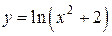 .
.
Переход от неявного задания к явному возможен далеко не всегда. Например, уравнение
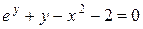
задаёт 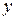 как неявную функцию переменной
как неявную функцию переменной 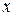 , но мы не можем перейти к ее заданию с помощью формулы.
, но мы не можем перейти к ее заданию с помощью формулы.
Не всякое уравнение задает неявную функцию, а некоторые – не одну. Например,:
1) уравнение
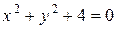
не задаёт неявную функцию;
2) уравнение
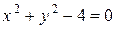
определяет две неявные функции, явные задания которых
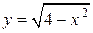 и
и 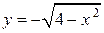 ;
;
3) уравнение
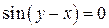
определяет бесконечно много неявные функции, явные задания которых
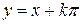 ,
,
где 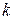 – произвольное целое число.
– произвольное целое число.
При каких условиях уравнение (1) задает неявную функцию 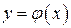 ? Имеет место следующая теорема существования неявной функции.
? Имеет место следующая теорема существования неявной функции.
Теорема 8.1. Пусть:
1) функции 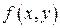 ,
, 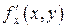 ,
, 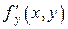 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 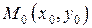 ;
;
2) 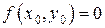 ;
;
3) 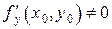 .
.
Тогда уравнение (1) определяет в некоторой окрестности точки 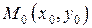 неявную функцию
неявную функцию 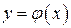 , непрерывную и дифференцируемую в некоторой окрестности точки
, непрерывную и дифференцируемую в некоторой окрестности точки 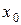 , причем
, причем 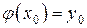 .
.
Производную неявной функции 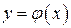 , особенно в тех случаях, когда невозможен переход к явному виду, вычисляют по формуле
, особенно в тех случаях, когда невозможен переход к явному виду, вычисляют по формуле
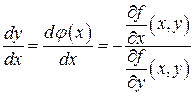 . (2)
. (2)
Пример 8.2. Найти производную неявно заданную функцию уравнением
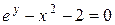 .
.
Решение. Полагая 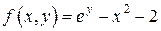 , имеем
, имеем
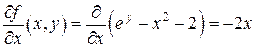 ,
,
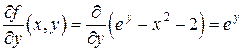 .
.
По формуле (2) получаем
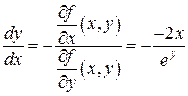 ,
,
учитывая уравнение 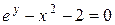 , получаем, что
, получаем, что 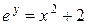 . Значит,
. Значит,
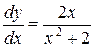 .
.
Найдем теперь производную, воспользовавшись явным заданием:
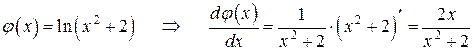 .
.
Ответ: 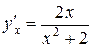 .
.
2. Функция двух переменных. Пусть 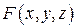 – функция трех переменных.
– функция трех переменных.
Аналогично теореме 8.1 можно сформулировать утверждение.
Теорема 8.2. Пусть:
1) функции 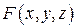 ,
, 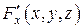 ,
, 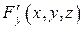 ,
, 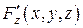 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 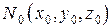 ;
;
2) 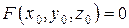 ;
;
3) 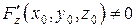 .
.
Тогда уравнение (1) определяет в некоторой окрестности точки 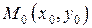 неявную функцию
неявную функцию 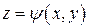 , непрерывную и дифференцируемую в некоторой окрестности точки
, непрерывную и дифференцируемую в некоторой окрестности точки 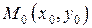 , причем
, причем 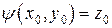 .
.
Для нахождения частных производных 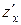 и
и 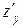 неявной функции
неявной функции 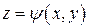 используются формулы, аналогичные формуле (2):
используются формулы, аналогичные формуле (2):
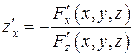 ,
, 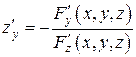 . (4)
. (4)
Пример 8.3. Найти 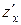 и
и 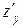 , если
, если
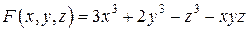 .
.
Решение. Имеем
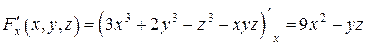 ,
,
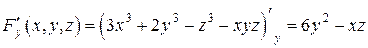 ,
,
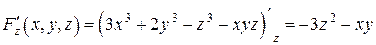 ;
;
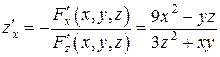 ,
,
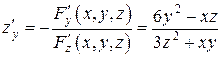 .
.
Ответ: 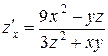 ,
, 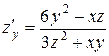 .
.
Дата добавления: 2020-04-12; просмотров: 392;











