Производная сложной функции. Полная производная
Пусть 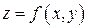 – функция двух переменных
– функция двух переменных 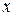 и
и 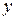 , каждая из которых является функцией независимой переменной
, каждая из которых является функцией независимой переменной 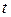 :
: 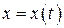 ,
, 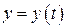 . В этом случае функция
. В этом случае функция 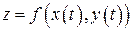 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной 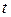 , а
, а 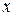 и
и 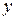 – промежуточными переменными.
– промежуточными переменными.
Теорема 7.1. Если функция 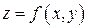 дифференцируемая в точке
дифференцируемая в точке 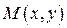 , а функции
, а функции 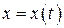 и
и 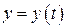 дифференцируемые по переменной
дифференцируемые по переменной 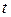 , то производная сложной функции
, то производная сложной функции 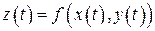 вычисляется по формуле
вычисляется по формуле
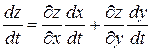 .
.
Пример 7.1. 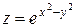 ;
; 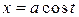 ,
, 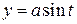 ; найти
; найти 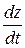 .
.
Решение. Имеем
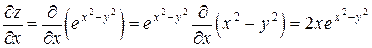 ,
,
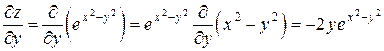 ,
,
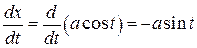 ,
,
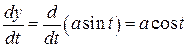 .
.
Подставим в формулу 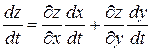 :
:
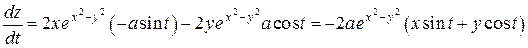 .
.
Выразив 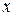 и
и 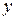 через
через 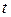 , получим
, получим
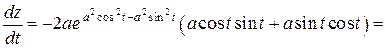
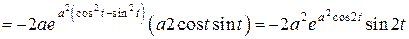 .
.
Ответ: 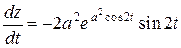 .
.
Частным случаем теоремы 7.1 является случай, когда 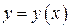 . Тогда функция имеет вид:
. Тогда функция имеет вид: 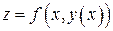 и является сложной функцией одной независимой переменной
и является сложной функцией одной независимой переменной 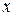 . Для производной сложной функции получаем формулу:
. Для производной сложной функции получаем формулу:
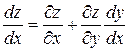 .
.
Эта формула носит название формулы полной производной.
Пример 7.2. 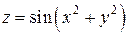 ;
; 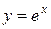 ; найти
; найти 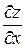 и
и 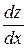 .
.
Решение. Имеем
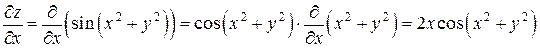 ,
,
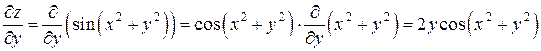 ,
,
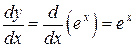 ,
,
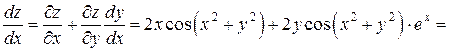
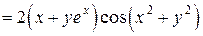 .
.
Выразив 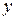 через
через 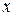 , получим
, получим
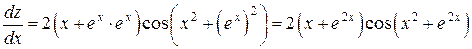 .
.
Ответ: 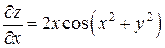 ,
,
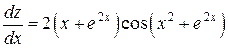 .
.
Рассмотрим общий случай. Пусть 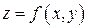 – функция двух переменных
– функция двух переменных 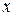 и
и 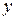 , каждая из которых является функцией двух независимых переменных
, каждая из которых является функцией двух независимых переменных 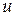 и
и 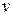 :
: 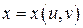 ,
, 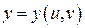 . Тогда
. Тогда 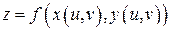 является сложной функцией двух независимых переменных
является сложной функцией двух независимых переменных 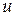 и
и 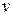 . Частные производные сложной функции
. Частные производные сложной функции 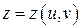 вычисляются следующими формулами:
вычисляются следующими формулами:
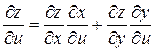 ,
,
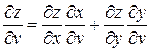 .
.
Пример 7.3. 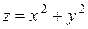 ;
; 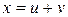 ,
, 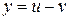 ; найти
; найти 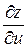 и
и 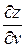 .
.
Решение. Имеем
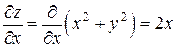 ,
,
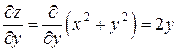 ,
,
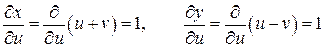 ,
,
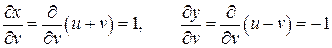 ;
;
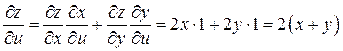 ,
,
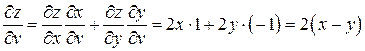 .
.
Выразив 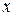 и
и 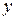 через
через 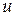 и
и 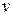 , получим
, получим
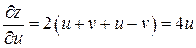 ,
,
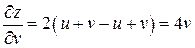 .
.
Ответ: 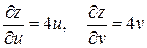 .
.
Пример 7.4. 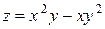 ;
; 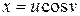 ,
, 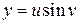 ; найти
; найти 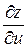 и
и 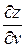 .
.
Решение. Имеем
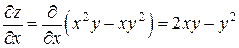 ,
,
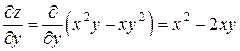 ,
,
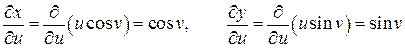 ,
,
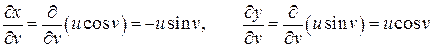 ;
;
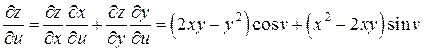 ,
,
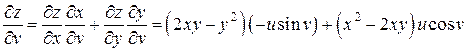 .
.
Выразив 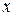 и
и 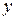 через
через 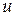 и
и 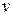 , получим
, получим
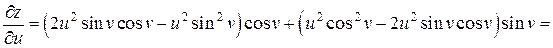
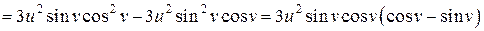 ,
,

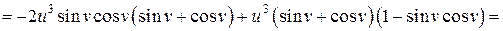
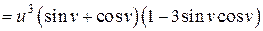 .
.
Ответ: 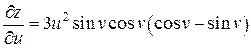 ,
,
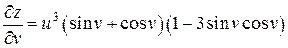 .
.
Дата добавления: 2020-04-12; просмотров: 390;










