Идеальный трансформатор
Будем считать, что сопротивления обмоток и потери энергии в сердечнике равны нулю, все магнитное поле сосредоточено в сердечнике, магнитная проницаемость сердечника стремится к бесконечности. Такая модель называется идеальным трансформатором. Она описывает работу трансформатора с точностью до нескольких процентов. Получим уравнения этой модели.
Рассмотрим двухобмоточный трансформатор (рис. 1.1). Примем, что индукция и напряженность магнитного поля связаны уравнением 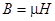 , где m - число.
, где m - число.
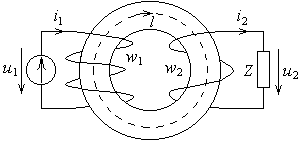 Рис. 1.1. Двухобмоточный трансформатор.
Рис. 1.1. Двухобмоточный трансформатор.
|
Примем также, что токи обмоток (а вследствие этого также напряженность магнитного поля, магнитная индукция и магнитный поток в сердечнике) – произвольные периодические функции времени с нулевой постоянной составляющей.
Введем обозначения: w1, w2 – число витков первичной и вторичной обмотки соответственно, l – длина средней линии сердечника, S – площадь поперечного сечения сердечника, Ф – магнитный поток в сердечнике.
По закону электромагнитной индукции
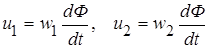 , (1‑1)
, (1‑1)
откуда 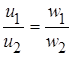 .
.
Это уравнение напряжений идеального трансформатора: напряжения обмоток пропорциональны числу витков.
По закону полного тока 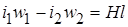 . (1‑2)
. (1‑2)
Так как индукция магнитного поля в сердечнике ограничена ( 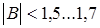 Тл),
Тл), 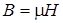 ,
, 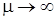 , то
, то 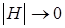 . Так как длина средней линии сердечника ограничена, то
. Так как длина средней линии сердечника ограничена, то 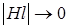 , поэтому из уравнения (1-2) получаем уравнение токов идеального трансформатора: токи обмоток обратно пропорциональны числу витков:
, поэтому из уравнения (1-2) получаем уравнение токов идеального трансформатора: токи обмоток обратно пропорциональны числу витков:
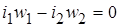 .
.
Из последнего уравнения следует, что ток холостого хода идеального трансформатора равен нулю (у реальных трансформаторов он составляет несколько процентов от номинального).
Отметим, что 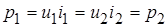 , то есть идеальный трансформатор мгновенную мощность источника полностью передает нагрузке.
, то есть идеальный трансформатор мгновенную мощность источника полностью передает нагрузке.
Число 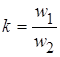 называется коэффициентом трансформации.
называется коэффициентом трансформации.
Вносимое сопротивление
Здесь и далее будем рассматривать трансформатор в синусоидальном режиме. Определим, как подействует на цепь первичной обмотки идеального трансформатора подключение к его вторичной обмотке сопротивления нагрузки Z. Для этого вычислим отношение напряжения и тока первичной обмотки:
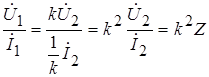 .
.
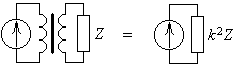 Рис. 1.2.
Рис. 1.2.
|
То есть, включение идеального трансформатора с нагрузкой Z в любую электрическую цепь эквивалентно непосредственному включению в эту цепь сопротивления 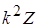 , которое называется вносимым сопротивлением (например, рис.1.2). Поэтому трансформаторы часто применяют для согласования сопротивления нагрузки Z с источником энергии, рассчитанным на подключение нагрузки
, которое называется вносимым сопротивлением (например, рис.1.2). Поэтому трансформаторы часто применяют для согласования сопротивления нагрузки Z с источником энергии, рассчитанным на подключение нагрузки 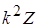 . Вносимое сопротивление – это простейшая модель трансформатора с нагрузкой. Оно называется также приведенным сопротивлением нагрузки.
. Вносимое сопротивление – это простейшая модель трансформатора с нагрузкой. Оно называется также приведенным сопротивлением нагрузки.
Упрощенная схема замещения трансформатора
Следующая по сложности модель трансформатора показана на схеме рис. 1.3. Она называется упрощенной, так как не учитывает ток холостого хода. Она позволяет рассчитать токи обмоток и напряжение нагрузки точнее, чем по уравнениям идеального трансформатора.
Сам трансформатор представлен сопротивлениями 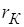 и
и 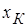 . Они определяют состояние цепи при коротком замыкании нагрузки, поэтому называются сопротивлениями короткого замыкания.
. Они определяют состояние цепи при коротком замыкании нагрузки, поэтому называются сопротивлениями короткого замыкания.
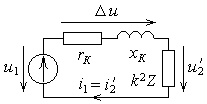 Рис. 1.3.
Рис. 1.3.
|
Резистор 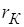 моделирует активные сопротивления обмоток. Индуктивное сопротивление
моделирует активные сопротивления обмоток. Индуктивное сопротивление 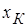 обусловлено магнитными потоками рассеивания обмоток (т.е. магнитным полем, выходящим за пределы сердечника).
обусловлено магнитными потоками рассеивания обмоток (т.е. магнитным полем, выходящим за пределы сердечника).
При замене сопротивления нагрузки Z вносимым сопротивлением k2Z оно включается в первичную цепь. Напряжение нагрузки увеличивается в k раз, а ток уменьшается в k раз. Это называется приведением нагрузки к первичной цепи. Напряжение 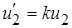 и ток
и ток 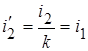 называются приведенными и отмечаются штрихами. Напряжение
называются приведенными и отмечаются штрихами. Напряжение 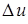 называется падением напряжения. Разность действующих значений напряжений
называется падением напряжения. Разность действующих значений напряжений 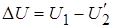 называется потерей напряжения. Ее значение используется для расчета напряжения нагрузки по заданному току. Обычно потеря напряжения составляет несколько процентов от номинального напряжения первичной обмотки.
называется потерей напряжения. Ее значение используется для расчета напряжения нагрузки по заданному току. Обычно потеря напряжения составляет несколько процентов от номинального напряжения первичной обмотки.
Опыт короткого замыкания
Для определения 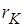 и
и 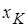 проводится опыт короткого замыкания (рис. 1.4). Сопротивление нагрузки заменяется перемычкой, а напряжение источника устанавливается таким, чтобы токи трансформатора были номинальными. Это напряжение называется напряжением короткого замыкания и обозначается UК.
проводится опыт короткого замыкания (рис. 1.4). Сопротивление нагрузки заменяется перемычкой, а напряжение источника устанавливается таким, чтобы токи трансформатора были номинальными. Это напряжение называется напряжением короткого замыкания и обозначается UК.
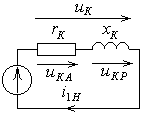 Рис. 1.4.
Рис. 1.4.
|
В паспортных данных трансформаторов указывают относительную величину 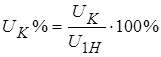 , где
, где 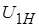 – номинальное напряжение первичной обмотки. В паспорте указывают также номинальные напряжения
– номинальное напряжение первичной обмотки. В паспорте указывают также номинальные напряжения 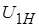 и
и 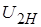 , мощность потерь энергии в опыте короткого замыкания PК и номинальную полную мощность SН. Номинальные токи
, мощность потерь энергии в опыте короткого замыкания PК и номинальную полную мощность SН. Номинальные токи 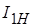 и
и 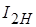 рассчитываются по паспортным данным.
рассчитываются по паспортным данным.
В опыте короткого замыкания измеряют напряжение, ток и потребляемую мощность первичной обмотки трансформатора. Сопротивления 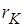 и
и 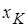 вычисляют по формулам
вычисляют по формулам
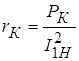 ,
, 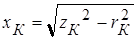 ,
,
т.к. 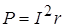 ,
, 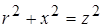 для любого двухполюсника. Здесь
для любого двухполюсника. Здесь 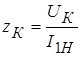 – полное сопротивление короткого замыкания.
– полное сопротивление короткого замыкания.
Внешняя характеристика трансформатора
Зависимость напряжения нагрузки от тока нагрузки называется внешней характеристикой трансформатора. Ее типичный график показан на рис. 1.5. Чтобы записать формулу для ее расчета, введем дополнительные обозначения:
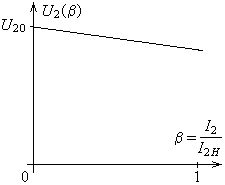 Рис. 1.5.
Рис. 1.5.
|
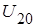 – напряжение холостого хода вторичной обмотки.
– напряжение холостого хода вторичной обмотки.
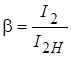 – коэффициент загрузки трансформатора,
– коэффициент загрузки трансформатора,
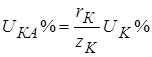 – относительное значение активной составляющей напряжения короткого замыкания (рис. 1.4),
– относительное значение активной составляющей напряжения короткого замыкания (рис. 1.4),
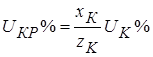 – относительное значение реактивной составляющей напряжения короткого замыкания (рис. 1.4),
– относительное значение реактивной составляющей напряжения короткого замыкания (рис. 1.4),
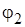 – разность фаз напряжения и тока нагрузки.
– разность фаз напряжения и тока нагрузки.
Внешняя характеристика трансформатора рассчитывается по формуле
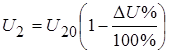 , (1‑3)
, (1‑3)
где относительная потеря напряжения 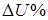 определяется так:
определяется так:
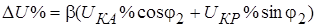 . (1‑4)
. (1‑4)
Вывод формулы для расчета внешней характеристики(на экзамен не выносится)
Вначале покажем, что потерю напряжения можно вычислить по формуле
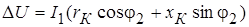 . (1‑5)
. (1‑5)
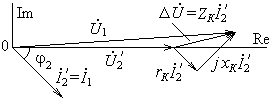 Рис. 1.6.
Рис. 1.6.
|
Рассмотрим векторную диаграмму напряжений и токов упрощенной схемы замещения трансформатора (рис. 1.6).
Начальную фазу напряжения нагрузки 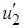 удобно принять равной нулю:
удобно принять равной нулю: 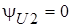 . Если разность фаз напряжения и тока нагрузки
. Если разность фаз напряжения и тока нагрузки 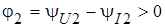 , то начальная фаза тока нагрузки
, то начальная фаза тока нагрузки 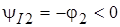 .
.
Фаза напряжения на резисторе 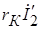 совпадает с фазой тока, фаза напряжения на катушке индуктивности
совпадает с фазой тока, фаза напряжения на катушке индуктивности 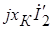 больше фазы тока на
больше фазы тока на 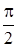 . Сумма этих напряжений равна падению напряжения:
. Сумма этих напряжений равна падению напряжения:
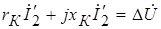 . (1‑6)
. (1‑6)
Кроме того, 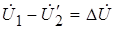 . (См. также рис. 1.3) (1‑7)
. (См. также рис. 1.3) (1‑7)
Нам нужно найти потерю напряжения (разность действующих значений)
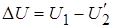 . (1‑8)
. (1‑8)
Выразим действующие значения напряжений через действительные и мнимые части их комплексов:
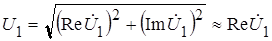 , (1‑9)
, (1‑9)
т.к. 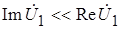 вследствие малости
вследствие малости 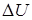 по сравнению с
по сравнению с 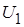 .
.
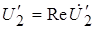 , т.к.
, т.к. 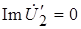 . (1‑10)
. (1‑10)
Подставляя формулы (1-9) и (1-10) в (1-8), получим:
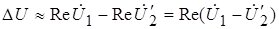 .
.
Из последнего уравнения с учетом (1-6) и (1-7) получим:
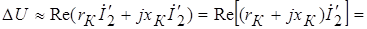
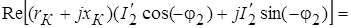
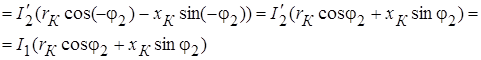 .
.
Из формулы (1-9) при номинальном значении первичного напряжения 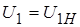 получим:
получим:
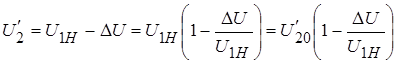 ,
,
где 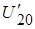 – приведенное напряжение холостого хода вторичной обмотки, оно равно напряжению
– приведенное напряжение холостого хода вторичной обмотки, оно равно напряжению 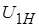 . Относительное изменение приведенного вторичного напряжения
. Относительное изменение приведенного вторичного напряжения 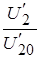 равно относительному изменению настоящего вторичного напряжения
равно относительному изменению настоящего вторичного напряжения 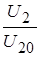 , поэтому
, поэтому
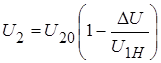 . (1‑11)
. (1‑11)
Если относительную потерю напряжения выразить в процентах 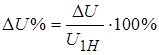 , то из формулы (1-11) получим выражение (1-3). Используя соотношения
, то из формулы (1-11) получим выражение (1-3). Используя соотношения 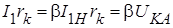 ,
, 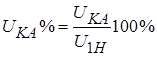 ,
, 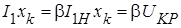 ,
, 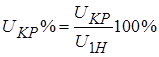 , формулу (1-5) можно привести к виду (1-4).
, формулу (1-5) можно привести к виду (1-4).
Полная схема замещения трансформатора
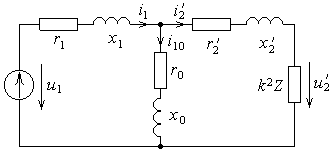 Рис. 1.7.
Рис. 1.7.
|
Чтобы учесть ток холостого хода трансформатора, к упрощенной схеме замещения нужно добавить еще одну ветвь (рис. 1.7). Она называется намагничивающей. По ней протекает ток холостого хода трансформатора. Резистор 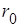 моделирует активное сопротивление, обусловленное потерями энергии в сердечнике трансформатора. Индуктивное сопротивление
моделирует активное сопротивление, обусловленное потерями энергии в сердечнике трансформатора. Индуктивное сопротивление 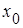 обусловлено магнитным потоком в сердечнике.
обусловлено магнитным потоком в сердечнике.
Резистор 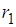 обозначает активное сопротивление первичной обмотки. Индуктивное сопротивление первичной обмотки
обозначает активное сопротивление первичной обмотки. Индуктивное сопротивление первичной обмотки 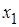 обусловлено ее магнитным потоком рассеивания. Приведенные сопротивления
обусловлено ее магнитным потоком рассеивания. Приведенные сопротивления 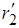 и
и 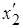 моделируют соответствующие параметры вторичной обмотки. Обычно трансформаторы конструируют так, что
моделируют соответствующие параметры вторичной обмотки. Обычно трансформаторы конструируют так, что 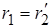 ,
, 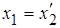 .
.
Дата добавления: 2020-03-21; просмотров: 1409;











