Основные формулы для определения скоростей и ускорений точек звеньев
Определение скоростей и ускорений точек звеньев при поступательном, вращательном и плоскопараллельном движениях.
Планы скоростей и ускорений. Принцип подобия в планах скоростейи ускорений. Примеры кинематического исследования механизмов.
Теоретические предпосылки определения скоростей и ускорений
Основные формулы для определения скоростей и ускорений точек звеньев механизмов приведены в таблице 3.1.
Планы скоростей и ускорений
Планом скоростей (ускорений) называется диаграмма, на которой от некоторого центра (полюса) в масштабе отложены векторы скоростей (ускорений) точек тела.
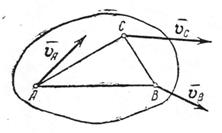
Рассмотрим тело, совершающее плоскопараллельное движение (рис.3.1).
Для плоскопараллельного движения скорости точек определяются по формулам:
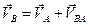 ,
, 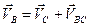 ,
, 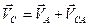 (3.1)
(3.1)
где 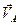 ,
, 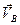 ,
, 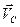 - абсолютные скорости точек А, В, С;
- абсолютные скорости точек А, В, С;
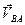 ,
, 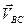 ,
, 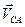 - относительные скорости.
- относительные скорости.
План скоростей получим, если в выбранном масштабе 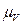 (
( 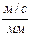 ) отложим от полюса
) отложим от полюса 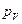 отрезки
отрезки 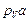 ,
, 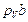 и
и 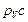 , параллельные векторам скоростей
, параллельные векторам скоростей 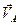
 ,
, 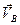 ,
, 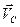 . Отрезки находятся по формулам:
. Отрезки находятся по формулам: 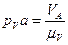 ,
, 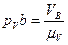 ,
, 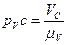 .
.
|
|
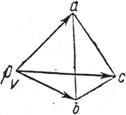
В результате построения плана скоростей получен треугольник авс (рис.3.2),который подобен треугольнику АВС. Относительных скоростей 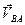 ,
, 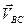 и
и 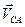 находятся по формулам:
находятся по формулам: 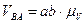
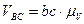 ,
, 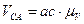 .
.
Рис.3.1 Рис.3.2
Сформулируем принцип подобия в плане скоростей:
В плане скоростей векторы относительных скоростей точек жесткого звена образуют фигуру, подобную звену, повернутую на угол 90° в сторону угловой скорости звена.
Следствие.
Пользуясь принципом подобия, достаточно на плане скоростей построить векторы скоростей только двух точек жесткого звена. Скорость же любой третьей точки определится путем построения фигуры или линии подобной данному звену.
Аналогично формулируется принцип подобия в плане ускорений.
Основные формулы для определения скоростей и ускорений точек звеньев
Таблица 3.1
| № | Вид движения | Скорость | Ускорение |
Поступательное
(ползун по стойке)
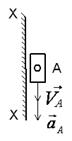
| Все точки звена имеют одинаковую скорость 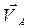 , вектор который направлен вдоль траектории движения точки A. , вектор который направлен вдоль траектории движения точки A.
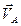 II Х-Х II Х-Х
| Все точки звена имеют одинаковые ускорения 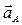 . Если вектор ускорения . Если вектор ускорения 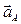 направлен в сторону направлен в сторону 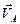 , то движение равноускоренное, если вектор ускорения , то движение равноускоренное, если вектор ускорения 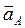 направлен в противоположнyю сторону направлен в противоположнyю сторону 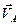 , то движение равнозамедленное. , то движение равнозамедленное.
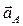 II Х -Хx II Х -Хx
| |
Вращательное вокруг неподвижной оси
(кривошип или коромысло относительно стойки)
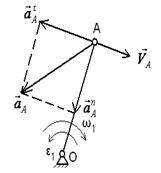
| Скорость точки А
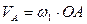 Вектор
Вектор 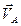 направлен перпендикулярно ОА, в сторону угловой скорости направлен перпендикулярно ОА, в сторону угловой скорости 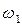 . .
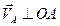
| Полное ускорение точки А
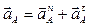 Нормальное ускорение
Нормальное ускорение 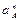 = = 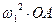 Вектор
Вектор 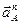 направлен по радиусу АО к центру вращения О. направлен по радиусу АО к центру вращения О.
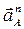 II OA.
Касательное ускорение II OA.
Касательное ускорение 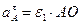 Вектор
Вектор 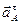 направлен перпендикулярно АО в сторону углового ускорения направлен перпендикулярно АО в сторону углового ускорения 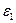
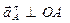
| |
Звено совершает плоскопараллельное движение
(шатун)
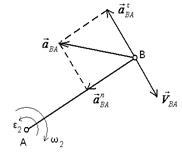
| Скорость точки В
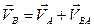 Относительная скорость
Относительная скорость
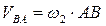 Вектор
Вектор 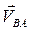 направлен перпендикулярно к ВА в сторону угловой скорости направлен перпендикулярно к ВА в сторону угловой скорости 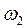 . .
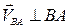
| Ускорение точки В
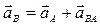 Относительное ускорение
Относительное ускорение
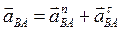 Нормальное ускорение
Нормальное ускорение
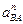 = = 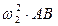 Вектор
Вектор 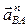 направлен параллельно АВ (от точки В к точке А) направлен параллельно АВ (от точки В к точке А)
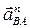 II ВА
Касательное ускорение II ВА
Касательное ускорение
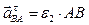 Вектор
Вектор 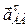 направлен перпендикулярно АВ направлен перпендикулярно АВ
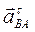 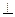 ВА ВА
|
Пример 3.1
Кинематический расчёт кривошипно-ползунного механизма. Определение скоростей точек звеньев для заданного положения механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и равна 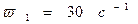 .
.
2).Размеры звеньев:
ОА = 20мм, АВ = 76мм, ВС = 26мм.
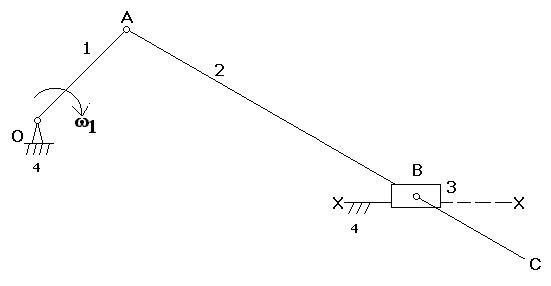
План скоростей 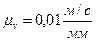
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, мм | Масштабный коэффициент μv | Значение величины, м/с |
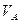
|  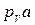
| 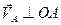 
| 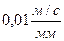 
| ||
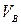
| 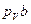
| 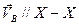
| |||
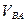
| 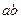
| 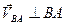
| |||
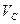
| 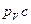
| ||||
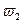
|
1. Определение скорости точки А.
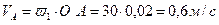 .
.
Вектор скорости 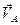 перпендикулярен кривошипу ОА.
перпендикулярен кривошипу ОА.
Выбираем масштаб плана скоростей 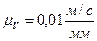 .
.
Найдём отрезок, изображающий вектор скорости 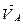 на плане:
на плане:
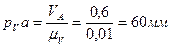 .
.
Из полюса плана скоростей 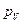 откладываем данный отрезок в направлении, перпендикулярном ОА в направлении угловой скорости
откладываем данный отрезок в направлении, перпендикулярном ОА в направлении угловой скорости 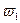 .
.
2. Определение скорости точки В.
Запишем векторное уравнение:
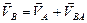 .
.
Направления векторов скоростей: 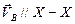 ,
, 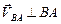 .
.
Продолжим строить план скоростей.
Из конца вектора 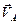 (точка
(точка 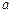 ) проводим направление вектора
) проводим направление вектора 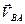 . Из полюса (точка
. Из полюса (точка 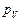 ) проводим направление вектора
) проводим направление вектора 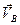 . На пересечении двух проведённых направлений получим точку
. На пересечении двух проведённых направлений получим точку 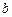 . Измеряя длины полученных отрезков и умножая их на масштаб
. Измеряя длины полученных отрезков и умножая их на масштаб 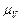 , получим значения скоростей:
, получим значения скоростей:
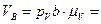
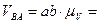
3. Определение скорости точки С.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
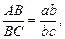
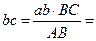 мм
мм
Данный отрезок откладываем на продолжении отрезка 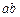 . Точку
. Точку 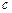 соединяем с полюсом
соединяем с полюсом 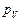 .
.
Величина скорости точки С:
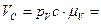

4. Определение угловой скорости шатуна АВ.
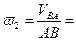 с-1
с-1
Для определения направления 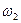 переносим вектор
переносим вектор 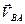 в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует
в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует 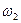 . В данном случае угловая скорость
. В данном случае угловая скорость 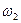 направлена против часовой стрелки.
направлена против часовой стрелки.
Пример 3.2
Кинематический расчёт кривошипно-коромыслового механизма. Определение скоростей точек звеньев для заданного положения механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и равна 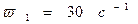 .
.
2).Размеры звеньев:
О1А = 20 мм, АВ = 50 мм, ВО2 = 30 мм, ВС = 25 мм.
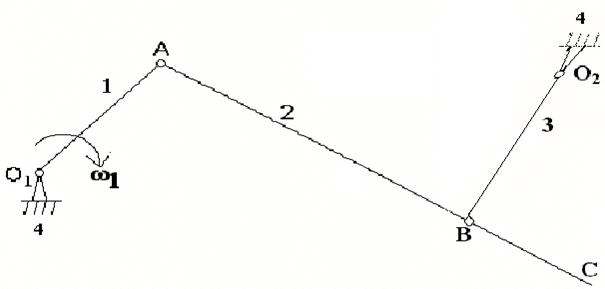
План скоростей 
| Исследуемая величина | Отрезок на плане | Направление | Величина отрезка на плане, мм | Масштабный коэффициент μv | Значение величины, м/с |
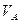
|  
| 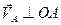 
| 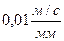 
| ||
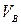
| 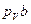
| 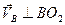
| |||
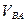
| 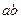
| 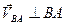
| |||
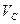
| 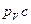
| ||||
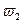
| |||||
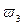
|
1. Определение скорости точки А.
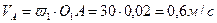 . Вектор скорости
. Вектор скорости 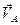 перпендикулярен кривошипу О1А.
перпендикулярен кривошипу О1А.
Выбираем масштаб плана скоростей 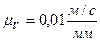 .
.
Найдём отрезок изображающий вектор скорости 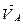 на плане:
на плане: 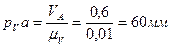 .
.
Из полюса плана скоростей 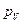 откладываем данный отрезок в направлении, перпендикулярном О1А в направлении угловой скорости
откладываем данный отрезок в направлении, перпендикулярном О1А в направлении угловой скорости 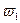 .
.
2. Определение скорости точки В.
Запишем векторное уравнение: 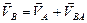 . Направления векторов скоростей:
. Направления векторов скоростей: 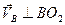 ,
, 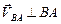 .
.
Продолжим строить план скоростей.
Из конца вектора 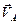 (точка
(точка 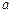 ) проводим направление вектора
) проводим направление вектора 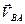 . Из полюса (точка
. Из полюса (точка 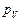 ) проводим направление вектора
) проводим направление вектора 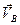 . На пересечении двух проведённых направлений получим точку
. На пересечении двух проведённых направлений получим точку 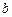 . Измеряя длины полученных отрезков и умножая их на масштаб
. Измеряя длины полученных отрезков и умножая их на масштаб 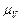 , получим значения скоростей:
, получим значения скоростей:
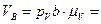
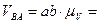
3. Определение скорости точки С.
Воспользуемся следствием из теоремы подобия. Составим пропорцию:
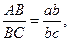
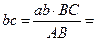
Данный отрезок откладываем на продолжении отрезка 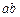 . Точку
. Точку 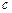 соединяем с полюсом
соединяем с полюсом 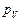 .
.
Величина скорости точки С: 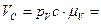

4. Определение угловой скорости шатуна АВ.
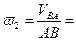
Для определения направления 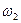 переносим вектор
переносим вектор 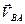 в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует
в точку В шатуна АВ и смотрим как она движется относительно точки А. Направление этого движения соответствует 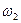 . В данном случае угловая скорость
. В данном случае угловая скорость 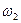 направлена против часовой стрелки.
направлена против часовой стрелки.
5. Определение угловой скорости коромысла ВО2.
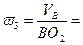
Для определения направления 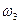 переносим вектор
переносим вектор 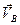 в точку В коромысла ВО2 и смотрим как она движется относительно точки О2. Направление этого движения соответствует
в точку В коромысла ВО2 и смотрим как она движется относительно точки О2. Направление этого движения соответствует 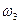 . В данном случае угловая скорость
. В данном случае угловая скорость 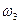 направлена против часовой стрелки.
направлена против часовой стрелки.
Пример 3.3
Дата добавления: 2016-06-22; просмотров: 5960;











