Оценка показателей надежности страховочных систем.

Теоретической базой расчета надежности систем страховки являются методы теории вероятности и математической статистики. При этом предполагается, что отказы появляются независимо друг от друга, в этой связи причины отказов действуют независимо друг от друга, поэтому событие «безотказная работа» можно рассматривать как сложное, заключающееся в отсутствии независимых отказов всех типов. При расчетах надежности образец системы страховки рассматривается как система, состоящая из параллельно и последовательно соединенных элементов.

Элементы в расчетной схеме показателей по надежности соединяются последовательно, если отказ системы наступает при отказе любого элемента. Если отказ системы наступает при отказе всех ее составных элементов, то последние соединяются параллельно.

Зная структуру системы, не трудно рассчитать ее показатели надежности по показателям надежности составляющих ее элементов. Вероятность безотказной работы параллельно и последовательно соединенных элементов можно выразить через вероятность безотказной работы составляющих элементов как:

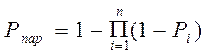, (2.1)

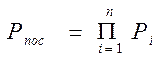, (2.2)

где, Р_пар – вероятность безотказной работы элементов, соединенных параллельно; Р_пос – вероятность безотказной работы элементов, соединенных последовательно; Р_i – вероятность безотказной работы каждого элемента системы.

При проведении спасательных работ используется верхняя и нижняя страховка. Страховочная система с верхней страховкой организуется различными способами. Верхняя нагруженная страховка может применяться только в сочетании с верхней ненагруженной страховкой.При таком виде страховки веревка постоянно находится под нагрузкой. Динамический рывок при срыве практически отсутствует. Первая страховочная цепь: верхняя нагруженная страховка – индивидуальная страховочная система-обвязка, закрепленная через спусковое устройство на статической несущей веревке. В случае отказа первой цепи, автоматически включается вторая цепь: верхняя ненагруженная страховка - динамическая веревка со страховкой сверху, или самостраховкой с помощью репшнура со схватывающим узлом или зажимом, сертифицированным для страховочных целей. Рывок, ограниченный длиной репшнура самостраховки, должен компенсироваться свойствами динамической веревки. Главное правило безопасности при этом способе самостраховки: место расположения схватывающего узла (или зажима) на страховочной веревке всегда должно быть выше точки закрепления петли репшнура на ИСС.

Страховочная система, организуемая в целях обеспечения самостраховки, является одним из вариантов верхней страховки. Для организации самостраховки при возможных остановках используется отрезок основной веревки, длина которого регулируется с помощью короткого отрезка репшнура со схватывающим узлом, закрепленного на ИСС.

Самостраховка таким же способом может быть организована за отдельную точку закрепления или за перила. Важно, чтобы она не стесняла движений, но при этом обеспечивала отсутствие рывка при возможной потере равновесия или срыве. Следовательно, точка закрепления самостраховки выбирается с учетом направления возможного рывка.

Организация верхней системы страховки начинается с включения ИСС спасателя в страховочную цепь. Если страховку осуществляет напарник, то перед началом работ страхующий проверяет правильность организации страховочной системы, ее исправность и сообщает об этом спускающемуся. Также необходимо самостоятельно проверить готовность системы к выполнению работ. Если спуск производится самостоятельно, необходимо, находясь на самостраховке, еще раз проверить надежность закрепления зажима или схватывающего узла на страховочной веревке и правильность закрепления ИСС альпиниста и только после этого отстегнуть самостраховку.

Существует много способов организации верхней страховки, однако базовая структура системы страховки постоянна. Рассмотрим пример расчета такой системы страховки. Схема по расчету надежности состоит из четырех основных элементов, соединенных последовательно (рис.2.1).

Рис.2.1. Схема по надежности страховочной системы при организации

Верхней страховки

Веревка, как элемент страховочной системы, подвержена внезапным отказам, в то время как ИСС, карабин и спусковое устройство подвержены преимущественно постепенным отказам. Так как элементы системы соединены последовательно, то вероятность безотказной работы данной страховочной системы Р(t)_сис может быть выражена как произведение вероятностей отсутствия внезапных отказов веревки [Р(t)_вн] и постепенных отказов ИСС Р_пос1, карабина Р_пос2, и спускового устройства Р_пос3:

Р(t)_сис = Р(t)_вн·Р(t)_пос1·Р(t)_пос2·Р(t)_пос3 . (2.3)

Следовательно, для того, чтобы рассчитать вероятность безотказной работы всей системы P(t), необходимо рассчитать вероятности безотказной работы каждого элемента системы Р(t)_вн и P_пос(t).

Вероятность возникновения внезапного отказа альпинистской веревки описывается экспотенциальным законом распределения:

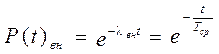, (2.4)

где t - время работы веревки в часах; Р_вн(t) - вероятность безотказной работы (отсутствие внезапных отказов) в течение заданного промежутка времени; l_вн – интенсивность отказов, то есть вероятность отказа образца в единицу времени при условии, что до этого момента отказ не наступал, ч^-1; Т_ср – среднее время наработки на отказ между двумя последовательными отказами или до первого отказа в часах.

Распределение времени безотказной работы при постепенных отказах, как и распределение значений прочностных показателей, описывается нормальным, а точнее, усеченным нормальным законом распределения, имеющим плотность распределения:

, (2.5)

где 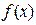- плотность нормального распределения; 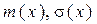- математические ожидание и среднее квадратичное отклонение значений параметра х (наработки на отказ, показателей прочностных свойств); 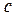- нормируемый множитель, учитывающий усеченность распределения и определяемый из условия:

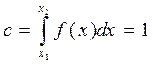. (2.6)

Вероятность отсутствия постепенных отказов при нормальном законе распределения у такого элемента страховочной цепи как индивидуальная страховочная система определяется следующим образом:

P(t) _пос1 = 1 - F(x), (2.7)

где F(x) – функция нормального распределения.