Гидравлические потери по длине
Потери напора по длине, иначе их называют потерями напора на трение 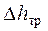 , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
, в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью
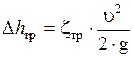 ,
,
где 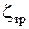 - коэффициент сопротивления, обусловленный трением по длине.
- коэффициент сопротивления, обусловленный трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
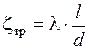 ,
,
где 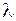 – коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления).
– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления).
Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
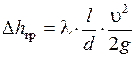 .
.

Рисунок 3.16 – Схема к определению коэффициента гидравлического трения
Для определения физического смысла коэффициента λ рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростью 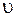 (рисунок 3.16). На этот объём действуют силы давления P1 и P2, причём P1 > P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы τ0. Условием равномерного движения под действием сказанных сил будет следующее равенство
(рисунок 3.16). На этот объём действуют силы давления P1 и P2, причём P1 > P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы τ0. Условием равномерного движения под действием сказанных сил будет следующее равенство
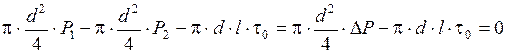
Если учесть, что
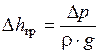 , то
, то 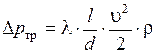 ,
,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим
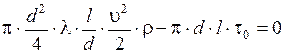 .
.
Преобразовав это выражение и выразив из него λ, окончательно будем иметь
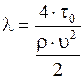 .
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков.
3.13.3 Течение жидкости в шероховатых трубопроводах
Исследование течения жидкости в шероховатых трубах практически полностью основываются на экспериментальных исследованиях. На их результатах основаны зависимости и расчётные формулы, применяющиеся для определения потерь энергии в подобных условиях. Основная формула для определения потерь напора – формула Дарси. Отличие заключается только в коэффициенте потерь на трение. В отличие от турбулентных потоков в гладких трубах, где коэффициент на трение полностью определяется числом Рейнольдса Re, для потоков в трубах имеющих шероховатые внутренние поверхности 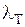 зависит ещё и от размеров этой шероховатости.
зависит ещё и от размеров этой шероховатости.
Установлено, что решающее значение имеет не абсолютная высота неровностей (абсолютная шероховатость) k (рисунок 3.17) а отношение высоты этих неровностей к радиусу трубы r0. Эта величина обозначается 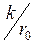 и называется относительной шероховатостью. Одна и та же абсолютная шероховатость может практически не влиять на коэффициент трения в трубах большого диаметра, и существенно увеличивать сопротивление в трубах малого диаметра. Кроме того, на сопротивление потоку жидкости влияет характер шероховатости.
и называется относительной шероховатостью. Одна и та же абсолютная шероховатость может практически не влиять на коэффициент трения в трубах большого диаметра, и существенно увеличивать сопротивление в трубах малого диаметра. Кроме того, на сопротивление потоку жидкости влияет характер шероховатости.

Рисунок 3.17 – Естественная шероховатость трубопровода
По характеру шероховатость разделяют на естественную(рисунок 3.17), при которой величина неровностей k по длине трубы различна, и регулярную(рисунок 3.18), при которой размеры неровностей по всей трубе одинаковы.

Рисунок 3.18 – Искусственная шероховатость трубопровода
Регулярная шероховатость создаётся искусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Регулярная шероховатость является следствием особенностей технологии изготовления труб, создаётся искусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Средняя шероховатость стальных новых труб равна 0,05 мм.
Коэффициент потерь на трение в этом случае описывается функцией
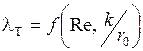 .
.
Эта зависимость проявляется в соотношении величины абсолютной шероховатости и величины ламинарного подслоя в потоке жидкости (рисунок 3.19).
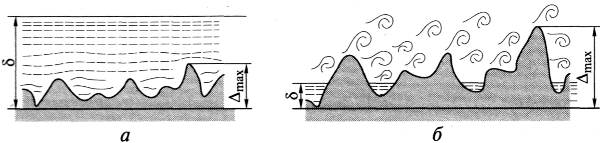
Рисунок 3.19 – Схемы течения жидкости
Экспериментальным изучением влияния числа Рейнольдса и относительной шероховатости занимался Никурадзе И. И., который проводил опыты для диапазонов 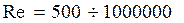 и
и 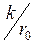 =1/500…1/15.
=1/500…1/15.
Результаты этих исследований сведены к графику в логарифмических координатах.
На графике (рисунок 3.20) цифрами обозначены:
1 – зона ламинарного течения, т.е. при Re < 2320, коэффициент гидравлического трения l зависит только от числа Рейнольдса и не зависит от относительной шероховатости. Т.к. величина ламинарного подслоя δ (рисунок 3.19) значительно больше величины шероховатости стенки. Поток жидкости плавно обтекает выступы, не давая образовываться вихревым зонам. Коэффициент гидравлического трения l определяется по формуле Пуазейля
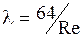 .
.
2 – зона турбулентного гладко стенного течения (область гидравлически гладких труб), 2320 < 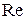 <
< 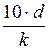 . Здесь выступы шероховатости k меньше толщины ламинарного подслоя d (рисунок 3.19) и коэффициент l зависит только от числа Рейнольдса. Коэффициент l может быть определен по формуле Конакова или Блазиуса:
. Здесь выступы шероховатости k меньше толщины ламинарного подслоя d (рисунок 3.19) и коэффициент l зависит только от числа Рейнольдса. Коэффициент l может быть определен по формуле Конакова или Блазиуса:
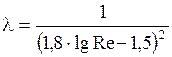 или
или 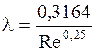 .
.
3 – зона, так называемого, доквадратичного течения
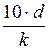 <Re<
<Re< 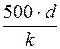 .
.
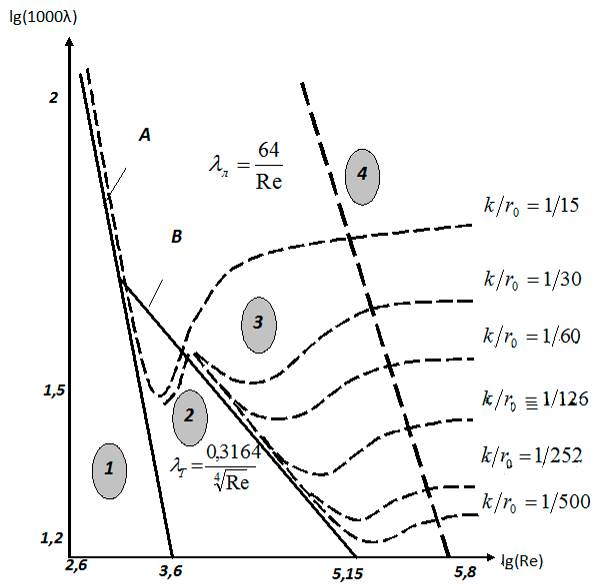
Рисунок 3.20 – Экспериментальный график Никурадзе
В этой области коэффициент l зависит как от числа Рейнольдса, так и от величины шероховатости 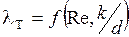 . Здесь выступы шероховатости k соизмеримы с толщиной ламинарного подслоя dл и начинают оказывать влияние на коэффициент гидравлического трения l. Коэффициент l может быть определен по формуле Альтшуля
. Здесь выступы шероховатости k соизмеримы с толщиной ламинарного подслоя dл и начинают оказывать влияние на коэффициент гидравлического трения l. Коэффициент l может быть определен по формуле Альтшуля
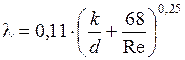 .
.
4 – зона квадратичного сопротивления 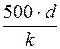 <Re. Здесь ламинарный подслой почти полностью разрушается, обнажая выступы шероховатости (рисунок 3.19). В этой области коэффициент сопротивления l является функцией только относительной шероховатости k/d и не зависит от числа Re. Коэффициент l определяется по формуле Никурадзе или Шифринсона
<Re. Здесь ламинарный подслой почти полностью разрушается, обнажая выступы шероховатости (рисунок 3.19). В этой области коэффициент сопротивления l является функцией только относительной шероховатости k/d и не зависит от числа Re. Коэффициент l определяется по формуле Никурадзе или Шифринсона
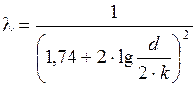

 или
или 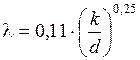
На практике для определения потерь напора в реальных шероховатых трубах чаще всего используют формулу Альдшуля.
Дата добавления: 2016-06-22; просмотров: 6483;











