Гидростатический парадокс
Рассмотрим три сосуда разной формы, заполненные жидкостью до одного уровня hc (рисунок 2.16). Все сосуды такие, что имеют одинаковую площадь дна.
В соответствии с общей формулой определения силы, действующей на плоскую поверхность можно вычислить силу, действующую на дно сосуда.
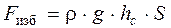 ,
,
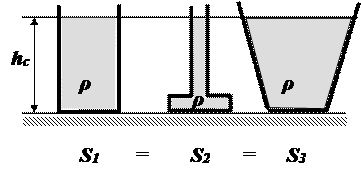
Рисунок 2.16 – Схема к определению гидростатического парадокса
Для всех трёх сосудов эти силы окажутся одинаковыми и независящими от веса жидкости в сосуде. Но на опору все сосуды будут действовать с разными силами, равными весу сосудов с жидкостью. Этот факт получил название гидростатического парадокса.
Тема 3
Гидродинамика
3.1Основные понятия
Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости (кинематика) и ее взаимодействие с твердыми телами при их относительном движении (динамика).
Кинематика жидкости изучает связь между геометрическими характеристиками движения и времени (скоростью и ускорением).
Динамика жидкости (или гидродинамика) изучает законы движения жидкости как результат действия сил и их применение в инженерной практике.
Течение жидкости может быть разделено на два основных вида: установившееся или неустановившееся.
Установившимся называют течение жидкости, неизменное по времени, при котором давление и скорость являются функциями только координат, и не зависят от времени (рисунок 3.1). Давление и скорость могут изменяться при перемещении частицы жидкости из одного положения в другое, но в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются во времени, т.е. 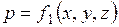 ;
; 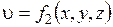 .
.

Рисунок 3.1 – Схема установившегося движения
Примером установившегося движения может служить истечение жидкости из сосуда, в котором поддерживается постоянный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.
Неустановившимся называют течение жидкости, все характеристики которого изменяются по времени в точках рассматриваемого пространства (рисунок 3.2).

Рисунок 3.2 – Схема неустановившегося движения
В общем случае неустановившегося течения давление и скорость зависят как от координаты, так и от времени
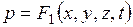 ;
; 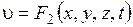 .
.
Примерами неустановившегося движения жидкости могут служить быстрое опустошение сосудов через отверстие в дне или движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение.
В гидродинамике рассматривают поток жидкости в целом – это непрерывная масса частиц жидкости, движущихся в определенном направлении.
При неустановившемся движении траектории различных частиц, проходящих через данную точку пространства, могут иметь разную форму. Установившееся движение может быть равномерным и неравномерным.
Равномерным движением называется такое, при котором скорости в сходственных точках двух смежных сечений равны между собой, а траектории частиц – прямолинейны и параллельны оси ох, т.е. поле скоростей не изменяется вниз по течению.
Все потоки имеют общие гидравлические элементы: линии тока, живое сечение, расход, скорость.
Свободная поверхность – это граница раздела жидкости и газа, давление на которой обычно равно атмосферному (рисунок 3.3, а).
Наличие или отсутствие её определяет тип потока: безнапорный или напорный.
Напорные потоки, как правило, наблюдаются в водопроводных трубах (рисунок 3.3, б) — работают полным сечением.
Безнапорные — в канализационных (рисунок 3.3, в), в которых труба заполняется не полностью, поток имеет свободную поверхность и движется самотёком, за счёт уклона трубы. Примерами напорного движения могут служить течения в трубопроводе с повышенным (или пониженным) давлением, в гидромашинах или других гидроагрегатах. Безнапорным – в реках, открытых каналах.
Свободной струей называется поток неограниченный твердыми стенками (например, истечение жидкости через отверстия из сосуда).
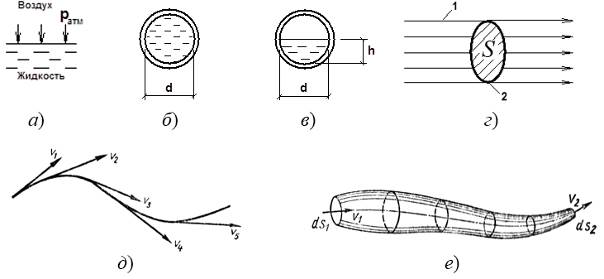
Рисунок 3.3 – Гидравлические элементы потока жидкости: а) свободная поверхность; б) напорный поток, в) безнапорный поток; д) линия тока; е) трубка тока;
1 – линия тока; 2 – живое сечение
В случае установившегося течения в процессе движения любая частица, попадая в заданное, относительно твёрдых стенок, место потока, всегда имеет одинаковые параметры движения. Следовательно, каждая частица движется по определённой траектории.
Траекториейназывается путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени.
При установившемся движении форма траекторий не изменяется во время движения. В случае неустановившегося движения величины направления и скорости движения любой частицы жидкости непрерывно изменяются, следовательно, и траектории движения частиц в этом случае также постоянно изменяются во времени.
Поэтому для рассмотрения картины движения, образующейся в каждый момент времени, применяется понятие линии тока.
Линией тока (рисунок 3.3, г и д) называется кривая, в каждой точке которой вектор скорости в данный момент времени направлен по касательной. В условиях установившегося течения линия тока совпадает с траекторией частицы и не меняет своей формы с течением времени.
Если в движущейся жидкости взять бесконечно малый замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока(рисунок 3.3, е). Часть потока, заключённая внутри трубки тока, называется элементарной струйкой.
Живым сечением(рисунок 3.3, г), или просто сечением потока, называется в общем случае поверхность в пределах потока, проведённая нормально к линиям тока.
Площадь живого сечения потока S (м2) — это площадь поперечного сечения потока, перпендикулярная линиям тока (рисунок 3.3, г).
Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу.
При установившемся движении элементарные струйки жидкости обладают рядом свойств:
· площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются линии тока;
· проникновение частиц жидкости через боковую поверхность элементарной струйки не происходит;
· во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения;
· форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться.
Трубка тока является как бы непроницаемой для частиц жидкости, а элементарная струйка представляет собой элементарный поток жидкости.
При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.
Местнойскоростью называется скорость частиц в данной точке потока. Скорость, определенная в некоторый момент времени, называется мгновенной, а среднее значение из достаточно большого числа измерений называется осредненной по времени скоростью.
В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения υS (рисунок 3.4). Индекс S означает (напоминает), что в каждой точке живого сечения скорости различны.

Рисунок 3.4 – Модель струйного движения
Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным S. Высота его в любой точке равна скорости соответствующей элементарной струйки υS. Площадь элементарной струйки равна dS. В пределах этой площади скорость можно считать постоянной.
3.2 Расход потока жидкости
Расход потока жидкости(расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока.
Различают объёмный, массовый и весовой расходы жидкости.
Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, дм3/с, л/с или л/мин. Он вычисляется по формуле
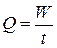 ,
,
где Q - объёмный расход жидкости,
W - объём жидкости, протекающий через живое сечение потока,
t – время течения жидкости.
Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле
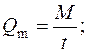
где 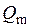 - массовый расход жидкости,
- массовый расход жидкости,
M - масса жидкости, протекающий через живое сечение потока.
Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так
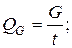
где QG - весовой расход жидкости,
G - вес жидкости, протекающий через живое сечение потока.
Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости dQ.
Если рассматривать поток жидкости как совокупность большого числа элементарных струек, то общий расход для всего потока можно определить как сумму элементарных расходов всех струек
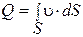 .
.
Для практических расчетов вводится понятие средней скорости потока жидкости или газа – скорости, с которой через данное живое сечение должны проходить все частицы жидкости, чтобы расход Q для данного сечения был равным расходу при действительных скоростях, неравномерно распределенных по сечению
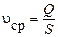 или
или 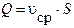 .
.
Среднюю скорость по живому сечению потока рассматривают как абстрактное понятие, позволяющее изучать поток как отдельную струйку.
При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.
3.3Закон сохранения массы. Уравнение неразрывности
Жидкость практически несжимаема и в ней невозможно образование пустот. Это условие сплошности или неразрывности потока жидкости.
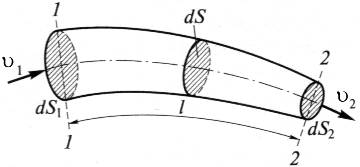
Рисунок 3.5 – Схема к определению расхода
Рассмотрим участок элементарной струйки (рисунок 3.5) ограниченный сечениями 1-1 и 2-2. количество жидкости, которое протекает внутри элементарной струйки за время dt, остается постоянным по ее длине. Через сечение 1-1 за время t войдет масса жидкости m1, а через сечение 2-2 за это время выйдет масса жидкости m2. Т.к. жидкость несжимаема, а стенки русла жесткие, то согласно закону сохранения вещества массы в сечениях равны
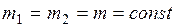 .
.
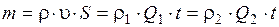 или
или 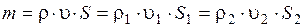
– это уравнение неразрывности потока для одномерного течения жидкости и газа.
При одномерном течении несжимаемой жидкости постоянным вдоль потока будет не только массовый, но и объемный расход. Если жидкость несжимаема, т.е. 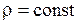 , то
, то 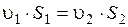 , следовательно
, следовательно
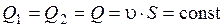 .
.
Это уравнение называется уравнением объемного расхода для потока несжимаемой жидкости (или уравнением постоянства расхода). Скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений
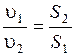 .
.
Скорости потоков воды в сетях водопровода и канализации зданий обычно порядка 1м/с.
3.4Уравнение Бернулли для установившегося движения идеальной жидкости
Жидкость, находящаяся в покое или движении, обладает определенным запасом механической энергии Е. Энергия определяет запас работы, которую может совершить тело, изменяя свое состояние. Работа – это произведение силы на перемещение под действием этой силы. Полная механическая энергия потока жидкости это сумма потенциальной и кинетической энергии. Причем покоящаяся жидкость обладает только потенциальной энергией, а движущаяся – потенциальной и кинетической. При этом потенциальная энергия складывается из энергии положения и потенциальной энергии давления. Т.е. полная механическая энергия определяется по формуле
Е = Епол + Едавл + Екин.
Удельной энергией жидкости называется энергия, отнесённая к единице массы.
Рассмотрим установившееся течение идеальной жидкости, находящееся под действием силы тяжести. Выделим элементарную струйку из потока жидкости. Обозначим сечения 1-1 и 2-2 заключив между ними участок струйки произвольной длины (рисунок 3.6). Пусть площадь первого сечения равна dS1, скорость в нём 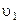 , давление р1, а высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости сравнения z1. Во втором сечении соответственно dS2,
, давление р1, а высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости сравнения z1. Во втором сечении соответственно dS2, 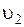 , р2 и z2.
, р2 и z2.
За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 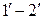 (рисунок 3.6).
(рисунок 3.6).
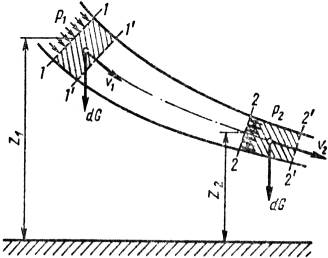
Рисунок 3.6 – Схема для вывода уравнения Бернулли
Следовательно, удельная механическая энергия (из законная сохранения энергии) для сечений 1 и 2 величина одинаковая и можно записать выражение
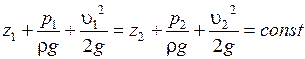 ,
,
Это уравнение Бернуллидля элементарной струйки идеальной несжимаемой жидкости, записанное в форме напоров.
Уравнение Бернулли можно записать в форме энергий или давлений
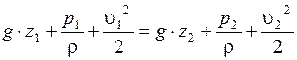
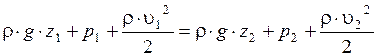
Дата добавления: 2016-06-22; просмотров: 4731;











