Сила давления жидкости на криволинейную стенку

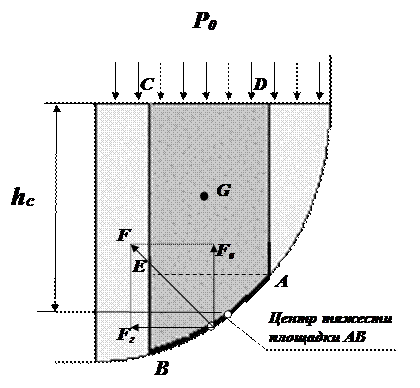
Рисунок 2.13 - Схема для определения силы внутреннего давления жидкости на криволинейную стенку

Чаще всего необходимо определить силу, действующую на цилиндрическую поверхность, имеющую вертикальную ось симметрии. Возможны два варианта. Первый вариант - жидкость воздействует на стенку изнутри (рисунок 2.13).

Во втором варианте жидкость действует на стенку снаружи (рисунок 2.14). Рассмотрим оба этих варианта.

В первом случае выделим объём жидкости (рисунок 2.13), ограниченный рассматриваемым участком цилиндрической поверхности AB, участком свободной поверхности CD, расположенным над участком AB, и двумя вертикальными поверхностями BC и CD, проходящими через точки A и B. Эти поверхности ограничивают объём ABCD, который находится в равновесии. Рассмотрим условия равновесия этого объёма в вертикальном и горизонтальном направлениях. Заметим, что, если жидкость действует на поверхность AB, c какой то силой F, то с такой же силой, но в обратном направлении, и поверхность действует на рассматриваемый объём жидкости. Эту силу, перпендикулярную поверхности AB, можно представить в виде горизонтальной F_г и вертикальной F_в составляющих.

Условие равновесия объёма ABCD в вертикальном направлении выглядит, так

,

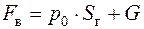где р₀ – внешнее давление,

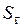– площадь горизонтальной проекции поверхности AB,

G – вес выделенного объёма жидкости.

Условие равновесия этого объёма в горизонтальной плоскости запишем с учётом того, что силы, действующие на одинаковые вертикальные поверхности AD и CE,взаимно уравновешиваются. Остаётся только сила давления на площадь BE, которая пропорциональна вертикальной проекции S_в поверхности AB. С учётом частичного уравновешивания условие равновесия сил в горизонтальном направлении равно

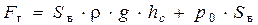
где h_с – глубина расположения центра тяжести поверхности AB.

ЗнаяF_г и F_в определим полную силуF, действующую на цилиндрическую поверхность

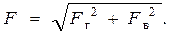
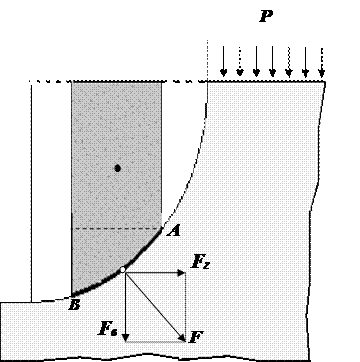
Рисунок 2.14 - Схема для определения силы внешнего давления жидкости на криволинейную стенку

Во втором случае, когда жидкость воздействует на цилиндрическую поверхность снаружи, величина гидростатического давления во всех точках поверхности AB имеет те же значения, что и в первом случае, т.к. определяется такой же глубиной. Силы, действующие на поверхность в горизонтальном и вертикальном направлениях, определяются по тем же формулам, но имеют противоположное направление. При этом под величиной G надо понимать тот же объём жидкости ABCD, несмотря на то, что на самом деле он, в данном случае и не заполнен жидкостью.

Положение центра давления на цилиндрической стенке легко можно найти, если известны силы F_г и F_в и определены центр давления на вертикальной проекции стенки и центр тяжести рассматриваемого объёма ABCD. Задача упрощается, если рассматриваемая поверхность является круговой, т.к. равнодействующая сила при этом пересекает ось поверхности. Это происходит из-за того, что силы давления всегда перпендикулярны поверхности, а перпендикуляр к окружности всегда проходит через её центр.

2.11Закон Архимеда. Плавание тел

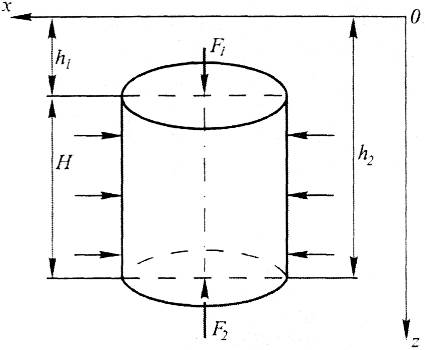
Рисунок 2.15 – Схема к закону Архимеда

Закон Архимеда определяет силу давления жидкости на поверхность погруженного в него тела. Предположим, что вертикальный цилиндр высотой H, с площадью основания S, погружен в жидкость (рисунок 2.15). При этом верхнее основание цилиндра погружено на глубину h₁, а нижнее – h₂. этот цилиндр находится под действием сил:

1) силы F₁действующей на верхнее основание цилиндра;

2) силы F₂,действующей на нижнее основание цилиндра;

3) сил гидростатического давления, действующих со всех сторон на вертикальную плоскость цилиндра и направленных нормально к его вертикальной оси (последние будут между собой уравновешиваться, так как они равны по величине и направлены в противоположные стороны).

Сила F₁нормальная к верхнему основанию цилиндра равна

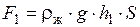
будет направлена сверху вниз. Сила F₁ будет стремиться погрузить тело в жидкость.

Сила F₂,нормальная к нижнему основанию цилиндра равна

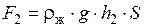
будет действовать снизу вверх. Сила F₂ будет стремиться вытолкнуть тело из жидкости.

Разность этих сил будет равна выталкивающей силе

,

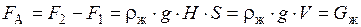которая равна весу объема жидкости, вытесненной телом, погруженным в жидкость.

Следовательно, закон Архимеда гласит: тело, погруженное в жидкость, находится под действием выталкивающей силы гидростатического давления, направленной снизу вверх и равной весу объема жидкости, вытесненной телом.

Разность между выталкивающей силой F_А и весом тела G_т, погруженным в жидкость, называется подъемной силой 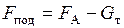, Н. В зависимости от соотношения этих сил возможны следующие случаи плавания тел:

1) F_А > G_т – тело всплывает на поверхность жидкости и плавает на поверхности в частично погруженном состоянии;

2) F_А < G_т – тело тонет;

3) F_А = G_т – тело плавает в полностью погруженном состоянии.