Электрохимические потенциалы

Если какой-либо металл соприкасается с электролитом, то на металле и в электролите появляются заряды противоположного знака. При этом металл приобретает относительно электролита определенный электрический потенциал, который называют электрохимическим потенциалом. Возникновение электрохимических потенциалов было объяснено Нернстом.

Электрохимический потенциал зависит от рода металла и концентрации электролита. При этом имеет значение только концентрация в растворе ионов самого металла, так как только ионы могут переходить между металлом и раствором. Наличие же других ионов в электролите не оказывает влияния на электрохимический потенциал.

Если концентрацию ионов металла в растворе поддерживать постоянной, то электрохимический потенциал будет зависеть только от рода металла и будет характеризовать его способность насыщать раствор ионами.

Любой гальванический элемент имеет два электрода. ЭДС гальванического элемента (напряжение при разомкнутой цепи) равна разности электрохимических потенциалов его электродов (j₁ - j₂).

Зная электрохимические потенциалы металлов, из которых состоят электроды, можно найти ЭДС химического источника тока.

ЭДС гальванического элемента это – максимальная работа химических реакций, рассчитанная на единицу заряда. Для приближенной оценки предполагается, что максимальная работа равна полной энергии, освобождаемой при химических реакциях. Тогда

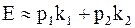, (7.49)

где p₁ и p₂ – тепловые эффекты реакций на обоих электродах (рассчитанные на 1 кг вещества электрода);

k₁ и k₂ – электрохимические эквиваленты вещества электродов.

Тепловые эффекты реакций на обоих электродах p₁ и p₂и электрохимические эквиваленты вещества электродов k₁ и k₂ можно представить в виде

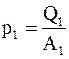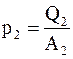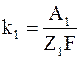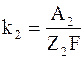; ; ; , (7.50)

где Q₁ и Q₂ – тепловые эффекты реакций на 1 килограмм-атом;

A₁ и A₂ – атомные веса материалов электродов;

Z₁ и Z₂ – валентности;

F – число Фарадея.

Тогда для ЭДС химического источника тока, будем иметь

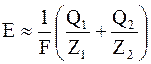. (7.51)

Надо отметить, что в гальванических элементах энергия, выделяемая в химических реакциях, непосредственно превращается в энергию электрического тока. Этот процесс обладает большим коэффициентом полезного действия, чем применяемый на обычных электростанциях. Поэтому гальванические элементы (химические источники тока) представляют большой принципиальный интерес.

Однако стоимость электроэнергии, получаемой от гальванических элементов, значительно выше стоимости энергии, вырабатываемой на обычных электростанциях, так как в элементах расходуется не дешевое топливо (например, уголь), а дорогостоящие вещества (например, цинк). В связи с этим химические источники тока (гальванические элементы) применяют только в тех случаях, где требуется небольшая энергия (где стоимость ее не играет роли), но важны портативность и простота источника тока.

При замыкании химического источника тока на внешнюю цепь сила тока в цепи не постоянна, а уменьшается с течением времени.

7.7. Электрический ток через электролиты.
Закон Ома для электролитов

Растворы солей, кислот и щелочей в воде и в других растворителях хорошо проводят электрический ток. Это связано с тем, что молекулы растворенного вещества диссоциируют, т.е. распадаются на положительные и отрицательные ионы. Если при растворении не происходит диссоциации молекул, то раствор не является проводником электрического тока.

Определим плотность тока j в жидкости, т.е. заряд, переносимый за одну секунду через площадку единичной площади, перпендикулярную направлению движения ионов (рис. 7.17). Так как перенос зарядов осуществляется ионами обоих знаков, то

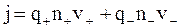, (7.52)

где q₊ и q_- – заряды положительных и отрицательных ионов;

n₊ и n_- – концентрации этих ионов;

v₊ и v_- – средние скорости упорядоченного движения этих ионов.

Учитывая, что раствор в целом нейтрален, можно записать

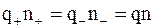, (7.53)

где q – заряд иона любого знака;

n – концентрация ионов этого же знака.

Величина заряда иона обусловлена потерей или сохранением валентных электронов при диссоциации молекулы. Обозначив валентность иона через z, для заряда иона будем иметь

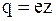, (7.54)

где e – абсолютное значение заряда электрона.

Учитывая формулы (7.53) и (7.54), получим

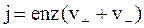. (7.55)

В электрическом поле на ионы действуют две силы: сила, действующая со стороны электрического поля, и сила внутреннего трения.

Сила со стороны электрического поля

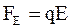, (7.56)

где E – величина напряженности электрического поля.

Сила внутреннего трения, если предположить, что ион имеет форму шара с радиусом r, то согласно закону Стокса

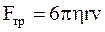, (7.57)

где h – коэффициент вязкости жидкости.

При установившемся движении (которое наступает практически одновременно с появлением электрического поля) F_E = F_тр, следовательно имеем

,

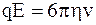откуда

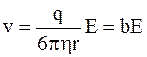, (7.58)

где 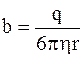– подвижность иона.

Таким образом, подвижность иона b равна отношению скорости движения иона к напряженности электрического поля:

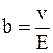. (7.59)

Как видно из формулы (7.58), подвижность ионов возрастает с повышением температуры (за счет уменьшения вязкости жидкости). Скорость движения ионов пропорциональна напряженности электрического поля.

Учитывая соотношение (7.58) для плотности электрического тока, получим

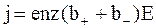(7.60)

или

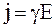, (7.61)

где 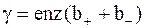- удельная проводимость электролита.

Выражения (7.60) и (7.61) представляют собой закон Ома в дифференциальной форме для электролитов.

Из формулы (7.60) для удельного сопротивления электролита имеем

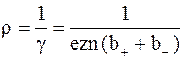. 7.62)

Так как с повышением температуры подвижность и концентрация ионов возрастают, то, согласно формуле (7.62), с повышением температуры сопротивление электролитов уменьшается.

Концентрация ионов зависит от степени диссоциации, характеризующейся коэффициентом диссоциации a. Коэффициент диссоциации определяется отношением концентрации n ионов к концентрации n_o молекул растворенного вещества:

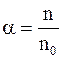. (7.63)

Откуда

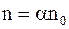. (7.64)

Концентрация недиссоциированных молекул

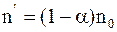. (7.65)

В растворе одновременно и непрерывно происходит как диссоциация молекул, так и молизация ионов, т.е. соединение ионов в нейтральные молекулы. В условиях равновесия интенсивности процессов диссоциации молекул и молезации ионов, изменяющих состав раствора в противоположных направлениях, равны. В процессе диссоциации молекул скорость изменения концентрации ионов каждого знака 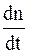пропорциональна концентрации n^' недиссоциированных молекул:

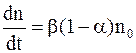, (7.66)

где b – коэффициент пропорциональности.

Скорость изменения концентрации недиссоциированных молекул 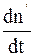в результате ионизации ионов пропорциональна произведению концентраций положительных и отрицательных ионов:

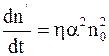, (7.67)

где h - коэффициент пропорциональности.

При равновесии 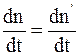, поэтому с учетом (7.66) и (7.67) можно получить формулу, связывающую коэффициент диссоциации с концентрацией растворенного вещества:

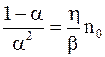. (7.68)

Очевидно, что коэффициент диссоциации зависит от концентрации растворенного вещества. При очень слабой концентрации (n_o » 0) равенство (7.68) дает

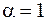. (7.69)

Если a<<1, то из (7.68) получаем

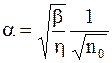. (7.70)

Таким образом, коэффициент диссоциации уменьшается при увеличении концентрации растворенного вещества.

С учетом 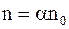уравнение для плотности тока в электролитах можно записать так:

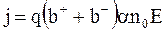. (7.71)

Подвижность ионов и коэффициент диссоциации в широких пределах изменения напряженности электрического поля не зависят от напряженности электрического поля E.

При небольшой концентрации раствора коэффициент диссоциации и сумма подвижностей ионов (b⁺ + b^-) приблизительно постоянны. Следовательно, при малой концентрации раствора электропроводимость пропорциональна концентрации. При увеличении концентрации зависимость электропроводности от концентрации значительно усложняется.

Надо отметить, что величина тока через столб электролита в любом его сечении одна и та же, хотя на первый взгляд она должна быть разной.

Представим, что имеется три сечения столба электролита 1, 2, 3 (рис. 7.18).

Через сечение 1 проходят только отрицательные ионы, через сечение 3 – только положительные ионы, а через сечение 2 – и те и другие. Поэтому создается впечатление, что ток через сечение 2 больше, чем через сечения 1 и 3. Это неверно, ток через любое сечение должен быть одним и тем же, иначе между сечениями будет накапливаться заряд. Выполнение закона сохранения заряда в электролитах обусловлено тем, что скорость упорядоченного движения и концентрация ионов разных знаков непостоянны вдоль выбранной оси ОХ.

В центральной области столба электролита концентрации положительных и отрицательных ионов примерно равны, следовательно, объемная плотность заряда близка к нулю. У положительного электрода (анода) скапливаются отрицательные ионы. Объемная плотность заряда отрицательна. У отрицательного электрода (катода) имеется положительный объемный заряд.

На рис. 7.19 показано изменение потенциала между электродами (при заданной разности потенциалов между ними), вызванное объемными зарядами. Сплошная линия соответствует изменению потенциала в вакууме, пунктирная – в том же пространстве, заполненном электролитом. На рис. 7.20 для сравнения показано изменение потенциала в межэлектродном промежутке, в который введены две сетки. Левая сетка заряжена отрицательно по отношению к аноду и имитирует отрицательный объемный заряд. Правая сетка заряжена положительно по отношению к катоду и имитирует положительный объемный заряд. Сравнение кривых изменения потенциала в межэлектродном пространстве показывает, что изменение потенциала в первом и втором случаях почти одинаково.

Постоянство величины электрического тока в электролитах обусловлено тем, что напряженность электрического тока, а следовательно, и скорость упорядоченного движения ионов в разных точках объема диэлектрика разные. В центральной области они меньше, чем в других областях.