Принцип суперпозиции электрических полей. Электрическое поле диполя

Если электрическое поле создано системой точечных зарядов: q₁, q₂, q₃,........., то в произвольной точке пространства "А" каждый из них порождает свое собственное поле с соответствующей напряженностью: E₁, E₂, E₃,......... . Результирующее поле в этом случае будет характеризоваться результирующим вектором напряженности электрического поля:

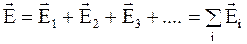. (1.6)

Величину и направление результирующего вектора напряженности E можно определить правилами геометрического сложения. Таким образом, для электрических полей оказывается справедливым принцип суперпозиции.

Воспользовавшись принципом суперпозиции электрических полей, можно определить напряженность электрического поля диполя, системы двух равных по величине, но противоположных по знаку зарядов (q₊ и q_-), расположенных на некотором расстоянии l друг от друга. В этом случае возможно решение двух задач:

Задача 1. Определить напряженность электрического поля в точке "А", лежащей на продолжении оси диполя, на расстоянии r>>l.

Задача 2. Определить напряженность электрического поля в точке "В", лежащей на перпендикуляре, восстановленном из центра диполя. Расстояние соответствующих точек до центра диполя r>>l.

Основной характеристикой диполя является его электрический дипольный момент p. Вектор pнаправлен от отрицательного заряда к положительному заряду. Он численно равен произведению заряда одного знака на плечо диполя (расстояние между центрами зарядов l<<r):

p = ql. (1.7)

Для решения задачи 1 необходимо сделать чертеж, подобный рис. 1.4.

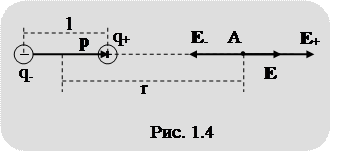На основании принципа суперпозиции электрических полей в точке "А" будет существовать электрическое поле с напряженностью

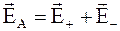. (1.8)

В численном виде

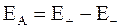. (1.9)

Так как

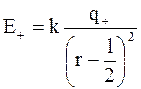, а ,

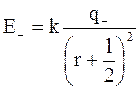то

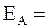
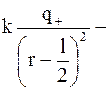
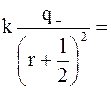
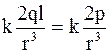, (1.10)

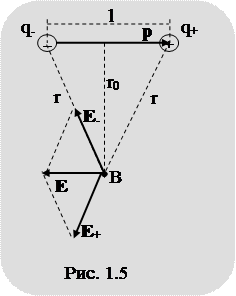где k = 1/(4p×e₀);

q₊ = q_-= q;

r – расстояние от центра диполя до рассматриваемой точки поля;

p = ql – электрический дипольный момент.

Для решения задачи 2 необходимо сделать чертеж, подобный рис. 1.5.

Имеем

,

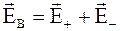где

,

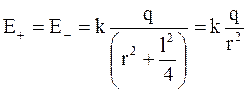так как r²>>l²/4.

Из подобия треугольников q_+, q_-,B и E_B, E₊,B

,

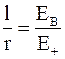откуда

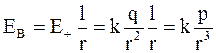. (1.11)

Можно показать, что в любой точке пространства напряженность электрического поля диполя

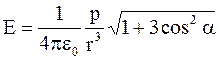, (1.12)

где a – угол между направлением вектора p и направлением на рассматриваемую точку поля.

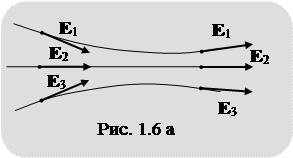Иногда электрические поля изображают графически с помощью силовых линий. Силовой линией электрического поля, линией вектора напряженности электрического поля, называют линию, проведенную в пространстве, касательная к которой в любой точке совпадает с направлением вектора E в данной точке. По густоте силовых линий можно судить о величине напряженности электрического поля в данном месте пространства, так как число силовых линий пропорционально напряженности электрического поля (рис. 1.6а).

Различают неоднородное электрическое поле и однородное электрическое поле.

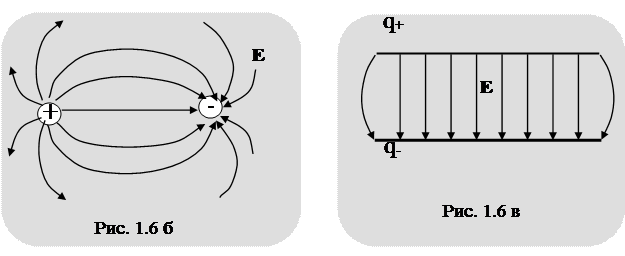
Характер распределения линий вектора напряженности неоднородного электрического поля, порождаемого двумя точечными зарядами, можно представить так, как показано на рис. 1.6б.

Характер распределения линий вектора напряженности однородного электрического поля, порождаемого двумя параллельными заряженными плоскостями, можно представить так, как показано на рисунке 1.6в.

В связи с тем, что в каждой точке поля вектор E имеет определенные направление и величину, силовые линии электрического поля не пересекаются.