Теплоемкость идеальных газов и их смесей
Под теплоемкостью рабочего тела в некотором процессе понимают количество тепла, которое необходимо подвести или отвести для того, чтобы изменить его температуру на 1 К:
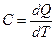 ,
, 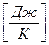
Теплоемкость единицы количества вещества называют удельной теплоемкостью. Различают удельные массовую 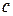 и мольную теплоемкости
и мольную теплоемкости 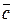 :
:
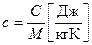 ;
; 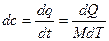 ;
; 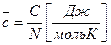
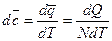
Между ними существует однозначная связь
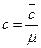
Теплоемкость газа зависит от характера процесса подвода теплоты и параметров. В зависимости от процесса теплоемкость любого газа может изменяться от 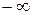 до
до 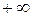 . В термодинамике широко используется понятия изобарной и изохорной теплоемкостей – это теплоемкости газа в соответствующих процессах (
. В термодинамике широко используется понятия изобарной и изохорной теплоемкостей – это теплоемкости газа в соответствующих процессах ( 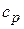 ,
, 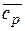 и
и 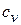 ,
, 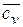 ) и их отношение
) и их отношение 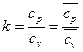 – показатель адиабаты.
– показатель адиабаты.
Теплоемкость идеальных газов зависит (в общем случае) от параметров 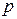 и
и 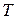 .
.
Согласно молекулярно-кинетической теории газа изобарные и изохорные теплоемкости идеального газа не зависят от параметров, а зависят только от числа степеней свободы молекул, иначе говоря – от природы газа, от его атомности.
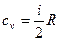
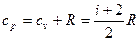
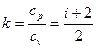
При частых расчетах показателя адиабаты чтобы не запоминать уравнения, можно пользоваться таблицей 3 (т.к. ряд простых чисел для запоминания удобнее).
Таблица 3. Расчет показателя адиабаты
| атомность (i) | 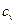
| 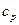
| 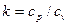
|
| одноатомный | 5/3=1,67 | ||
| двухатомный | 7/5=1,4 | ||
| трех и многоатомный | 9 (8) | 9/7=1,28 (8/7=1,14) |
Между изохорной, изобарной теплоемкостями и показателем адиабаты существует однозначная связь через уравнение Майера:
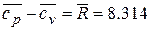 , или
, или 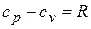
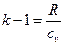 ,
, 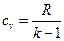 ,
, 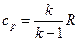
Для реальных газов теплоемкость зависит ещё и от физической природы и параметров, прежде всего от температуры. С ростом температуры теплоемкость реальных газов чаще всего увеличивается, показатель адиабаты уменьшается.
Найдем, чему равны теплоемкость и показатель адиабаты смеси газов.
Пусть имеем смесь, состоящую из n компонент: 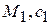 ;
; 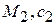 …
… 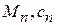 . Вся смесь нагревается в некотором диапазоне температур ΔТ. Тогда для каждой компоненты можно записать:
. Вся смесь нагревается в некотором диапазоне температур ΔТ. Тогда для каждой компоненты можно записать:
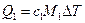
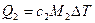
…
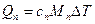
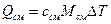
Теплота, переданная смеси, равна сумме теплот, переданных компонентам этой смеси, при этом каждая компонента нагревается на одну и ту же температуру ΔТ:
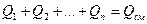
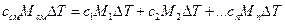
Поделив правую и левую части этого выражения на произведение МсмΔТ получаем:
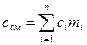
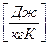
Аналогично для удельных мольных теплоемкостей
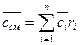
Таким образом, показатель адиабаты для смеси газов определяется следующим образом:
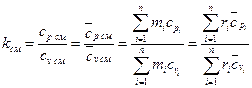
Дата добавления: 2020-03-21; просмотров: 924;











