СВЕРХПРОВОДНИКИ В ПРИБОРАХ ГРАВИМЕТРИИ И НАВИГАЦИИ
Значительная часть работ этого направления проводится в рамках Международного геодезического и геофизического союза. Они велись и ведутся в СССР, России [2.1], США [2.2], Канаде [2.3], Японии [2.4], Австралии [2.5], а также Норвегии, Венгрии и некоторых других странах.
Данные о гравитационном поле Земли получают с помощью ряда способов и систем:
- лазерного слежения за движением спутников Земли,
- астрофизического нивелирования,
- гравиметрии,
- градиентометрии,
- инерциальных навигационных систем и др.
В ряде стран разрабатываются навигационные системы и в области вооружений, например, в США [6]. В них основой навигационного обеспечения чаще всего ракетных атомных подводных лодок являются инерциальные навигационные системы.
Известно, что поле тяготения обладает основным свойством: все тела независимо от их массы движутся в этом поле при заданных начальных условиях одинаковым образом, и, следовательно, определив закон пробной массы, можно найти значение производных потенциала. Именно это свойство гравитационного поля позволяет строить баллистические приборы, измеряющие первую и вторую производные гравипотенциала. Первую производную принято называть ускорением свободного падения (УСП) (притяжением, силой притяжения, напряженностью), и ее измеряют с помощью гравиметров, а вторую производную называют градиентом УСП и измеряют с помощью градиентометров.
Методы измерения УСП делятся на динамические, в которых ведут наблюдение за движением пробного тела в поле тяготения, и статические, когда наблюдают положение равновесия пробного тела, на которое действуют две силы: сила тяжести и точно измеренная компенсирующая сила. По принципу статического измерения УСП построено большое число разнообразных приборов, различие которых заключается в выборе природы силового воздействия, компенсирующего силу тяжести.
В последние годы наибольшее внимание уделяется баллистическим методам. Перспективность их объясняется высокой точностью 1010, высокой надежностью получаемых результатов.
Существуют гравиметры на неподвижном основании: стационарные и переносные, а также на подвижном основании, например, на борту судна их называют набортными.
Еще есть градиентометры – это устройства, с помощью которых измеряют градиенты силы тяжести. Чтобы измерить градиенты всех составляющих силы тяжести, на стабилизированную платформу необходимо установить три градиентометра.
Таким образом, основу этих гравиинерциальных и инерциальных навигационных систем составляют гравиметры, акселерометры, градиентометры и гироскопы, к рассмотрению которых мы переходим. В данной главе представлены приборы, включающие такие сверхпроводящие элементы, как подвижное тело, экраны и др.
2.1. Гравиметры
Слово гравиметр происходит от латинского qravis –тяжелый и греческого metreo – измеряю, т.е. это прибор для измерения ускорения свободного падения под действием силы тяжести. Различают абсолютные и относительные измерения силы тяжести. Для абсолютных измерений ускорения силы тяжести g применяются баллистические гравиметры , точность которых составляет 0,01 мГал.
Относительные измерения силы тяжести производятся на суше:
а) маятниковыми гравиметрами (точность 0,03 – 0,05 мГал);
б) пружинными гравиметрами (точность 0,01 – 0,03 мГал).
Развитие гравиметрии [2.7] связано с исследованиями, например, геодинамических процессов, происходящих на нашей планете – в атмосфере, земной коре, мантии и ядре. С этими процессами связаны такие проблемы, как изучение движения континентов, перемещений земных полюсов, вертикальных и горизонтальных движений земной коры, разведки полезных ископаемых и т.д. Рассмотрим принцип действия основных гравиметров.
Любой гравиметр в своем составе имеет подвижный элемент (пробное тело, инерционное тело), который воспринимает полезный сигнал и под его действием изменяет свое пространственное положение вдоль оси чувствительности.
Изменения положения подвижного элемента осуществляются относительно неподвижного корпуса. При этом само пробное тело может быть закреплено на корпусе (приборы с контактным подвесом), а может быть вывешено с помощью сил различной физической природы относительно корпуса без контакта (приборы с неконтактным подвесом).
2.1.1. Гравиметры с контактным подвесом
Гравиметры могут быть механические, применяемые для сплошных гравиметрических съемок. К ним относятся маятниковые и пружинные.
2.1.1.1. Маятниковые гравиметры
Первым методом измерения ускорения силы тяжести был метод свободных колебаний маятника. Связь периода (Т) таких колебаний с ускорением свободного падения (g) математического маятника записывается в виде бесконечного ряда:
Т = 2π 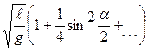 , (2.1)
, (2.1)
где ℓ - длина нити, α – амплитуда.
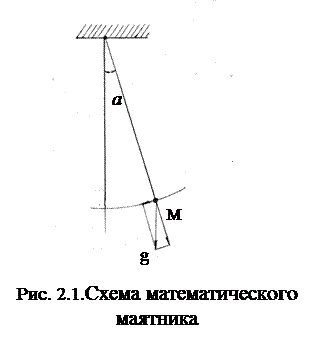 Вспомним, что под математическим маятником подразумевается идеальный маятник, состоящий из точечной массы, подвешенной на невесомой и нерастяжимой нити в абсолютном вакууме. Маятник, включающий физическое тело, качающийся около вертикальной оси, называется физическим маятником. Такой маятник совершает колебания по тому же закону, только роль длины ℓ в формуле (2.1) выполняет некоторая функция формы массы и расположения точки подвеса. Эта функция называется приведенной длиной маятника и имеет вид (рис.2.1)
Вспомним, что под математическим маятником подразумевается идеальный маятник, состоящий из точечной массы, подвешенной на невесомой и нерастяжимой нити в абсолютном вакууме. Маятник, включающий физическое тело, качающийся около вертикальной оси, называется физическим маятником. Такой маятник совершает колебания по тому же закону, только роль длины ℓ в формуле (2.1) выполняет некоторая функция формы массы и расположения точки подвеса. Эта функция называется приведенной длиной маятника и имеет вид (рис.2.1)
ℓ = 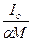 , (2.2)
, (2.2)
где Iо = 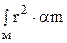 - момент инерции относительно оси качания,
- момент инерции относительно оси качания,
ℓ– расстояние от оси качания до центра тяжести, М – масса маятника.
Второй член в формуле (2.1) равен 7∙10-7 при практически применяемых амплитудах α ≤ 0,5о. Его можно рассматривать как поправку на неизохронность, остальные члены ряда пренебрежимо малы. Тогда формула (2.1) принимает вид
Т = 2π 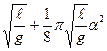 . (2.3)
. (2.3)
В формуле (2.3) второй ее член вводится как поправка за амплитуду, а колебания маятника могут рассматриваться как независящие от амплитуды. Обычно производят с маятниками относительные измерения, при которых исключается необходимость измерения длины маятника, она считается постоянной.
В качестве примера рассмотрим измерения для двух точек с gо и g при одинаковых остальных условиях:
для первой точки То = 2 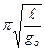 ;
;
для второй Т = 2 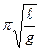 .
.
Возведя обе части уравнения в квадрат и разделив их, получим
g = go 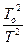 . (2.4)
. (2.4)
Искомое g представляют как разность периодов Т – То = ∆Т,
тогда запишем
g = go 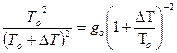 . (2.5)
. (2.5)
Разложив правую часть (2.5) в ряд, получим
g ~ go – 2go 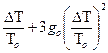 .
.
Последнее слагаемое мало, поэтому получаем
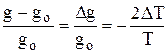 . (2.5*)
. (2.5*)
Допустим, что go= 980 Гал*, То = 0,496 с, ∆g = 0,001 Гал.
Тогда из (2.5*) получим
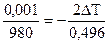 .
.
Откуда ∆Т = - 2,53 ∙10-7с, т.е. при увеличении g на 1 мГал период колебаний маятника уменьшается на 2,53 ∙10-7с.
2.1.1.2. Пружинные гравиметры
Схема, поясняющая принцип работы, показана на рис. 2.2.
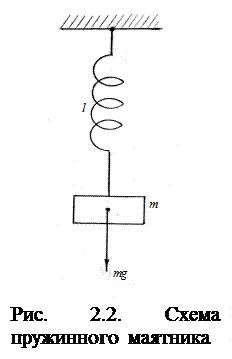 На пружине длиной ℓ подвешена масса m в гравитационном поле напряженности g, на нее действует сила F1 = mg. Противодействующей силой служит сила упругости пружины, которая по закону Гука записывается как
На пружине длиной ℓ подвешена масса m в гравитационном поле напряженности g, на нее действует сила F1 = mg. Противодействующей силой служит сила упругости пружины, которая по закону Гука записывается как
F2 = σ ∆ℓ,
где σ – коэффициент упругости, ∆ℓ - удлинение пружины.
В условиях равновесия обе силы равны, т.е.
σℓ = mg . (2.6)
____________________________________________________________
* Галл (Гал) – внесистемная единица измерения ускорения свободного падения. 1Гал = 1 см/с2 = 0,981 ~ 10-3g
Пусть в исходной точке g = go, длина пружины ℓо, при переходе в другую точку гравитационного поля g = g1, пружина будет иметь длину ℓ1. Изменение длины пружины допустим ℓ1-ℓо= ∆ℓ связано с изменением g на g1 –go = ∆g. Тогда в соответствии с условием (2.6) запишем
σ∆ℓ = m ∆g.
Откуда ∆g = 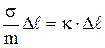 . (2.7)
. (2.7)
Удлинение пружины весов (∆ℓ) пропорционально (к )приращению силы тяжести и шкала прибора, естественно, линейна.
В структурных схемах такой простейший гравиметр можно представить, как показано на рис.2.3.
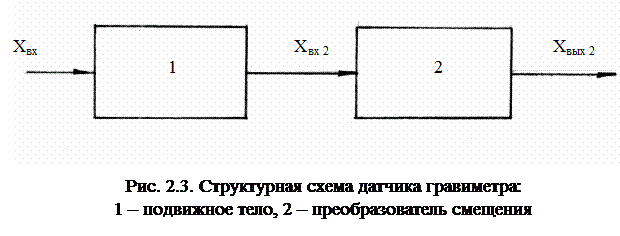 |
В соответствии с преобразованиями Лапласа для элементов систем автоматического управления (САУ) запишем
Хвых = WLXвх,
для данного ЧЭ передаточная функция (пропорциональное звено) имеет вид
WL = 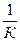 ,
,
подставив значение WL, получим
Хвых = 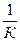 Хвх.
Хвх.
Если ввести обозначения в происходящие изменения длины пружины как ∆Z и причину изменения результирующей силы как ∆F, тогда запишем основные параметры пружинного гравиметра (ЧЭ-пружина):
жесткость
С =  , (2.8)
, (2.8)
чувствительность
r = 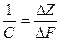 . (2.9)
. (2.9)
Любые гравиметры, выполненные из нормальных металлов, имеют недостатки, главный из них дрейф нуль – пункта, который ограничивает точность измерений и область применения этих приборов. Смещение нуль - пункта -следствие необратимых изменений, происходящих в материале подвеса, из которого изготовлена упругая система гравиметра, и полностью устранить его в системе не удается. Дрейф нуль -пункта зависит от изменений температуры окружающей среды, усталости материала упругого элемента, в данном случае - пружины. Нуль-пункт смещается в различных системах от 10-7 до 10-5 g в сутки. Это нежелательное явление уменьшают различными способами, однако полностью его устранить можно лишь с помощью бездиссипативной упругой системы, которую осуществляют, используя сверхпроводники.
2.1.2. Гравиметры с неконтактным подвесом
Впервые подобный подвес, состоящий из постоянного магнита и диска из свинца, охлажденного до температур жидкого гелия, был изучен в 1945г. В.К. Аркадьевым. В 1961г. появилась работа Бухгольда, где предлагалось использовать сверхпроводники для магнитных подвесов, и он не только создал первый вариант акселерометра (см. рис. 2.23 [2.15]), но и применил его. В своей работе он использовал упрощенное выражение для силы, действующей на единицу поверхности сверхпроводника со стороны магнитного поля. В системе СГС оно имеет вид (как и в работе Бухгольда)
F = 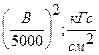 , (2.10)
, (2.10)
[B] –Гаусс (Гc),
в системе СИ
F = 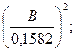
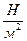 .
.
Например, сила, развиваемая катушкой шириной ℓо и средним радиусом r, равна
F1 = S ∙ F = 2πr ∙ ℓо ∙ F = 2πr ∙ ℓо ∙ 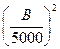 . (2.10, а)
. (2.10, а)
В однокатушечном подвесе, содержащем сверхпроводящий диск 1, короткозамкнутую сверхпроводящую обмотку 2 в виде тора (рис. 2.4, а) и охлажденном до температуры жидкого гелия, наводится ток I. В катушке индуктивностью L возникает магнитный поток Ф = L∙I. Этот поток Ф связан с катушкой, как показано на рисунке: его тангенциальная составляющая в зазоре величиной δ характеризуется магнитной индукцией В = Фо/Sδ, где Sδ – площадь, образуемая боковой поверхностью цилиндра высотой δ и длиной его окружности радиуса r1, т.е. Sδ = 2πr1∙ δ. При снижении диска в вертикальном направлении уменьшается индуктивность катушки и увеличивается ток (магнитный поток остается неизменным). Увеличение тока приводит к увеличению магнитной индукции, а следовательно, увеличению выталкивающей силы F1 (2.10), стремящейся восстановить прежнее его положение. При равновесии сумма сил, действующих на диск, равна нулю. Подвес такой конструкции не имеет боковой устойчивости и поэтому практически не используется.
В настоящее время созданы подвесы различных конструкций, некоторые из них мы рассмотрим в этой главе. Ранее мы отметили, что кроме выталкивающей силы подвес характеризуется жесткостью, для обозначения которой воспользуемся записью (2.8). С = 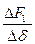 , где ∆δ –изменение зазора.Отметим еще одну важную особенность сверхпроводников – проводить электрический ток без сопротивления, которая используется и в подвесах. Если выводы сверхпроводящего провода катушки, идущие к источнику питания, зашунтировать также сверхпроводником и во время запитки катушки разрушить сверхпроводимость шунта источником тепла, а после запитки убрать этот источник тепла, тогда ток в катушке будет течь по шунту, минуя источник тока, и его можно выключить. Такой вариант, как мы помним, называется режимом «замороженного потока». Один из вариантов такого шунта показан на рис. 2.4,б. Он представляет собой проволочку из сверхпроводника, навитую на резистор и приваренную точечной сваркой к токовым выводам катушки. Через резистор пропу-
, где ∆δ –изменение зазора.Отметим еще одну важную особенность сверхпроводников – проводить электрический ток без сопротивления, которая используется и в подвесах. Если выводы сверхпроводящего провода катушки, идущие к источнику питания, зашунтировать также сверхпроводником и во время запитки катушки разрушить сверхпроводимость шунта источником тепла, а после запитки убрать этот источник тепла, тогда ток в катушке будет течь по шунту, минуя источник тока, и его можно выключить. Такой вариант, как мы помним, называется режимом «замороженного потока». Один из вариантов такого шунта показан на рис. 2.4,б. Он представляет собой проволочку из сверхпроводника, навитую на резистор и приваренную точечной сваркой к токовым выводам катушки. Через резистор пропу-
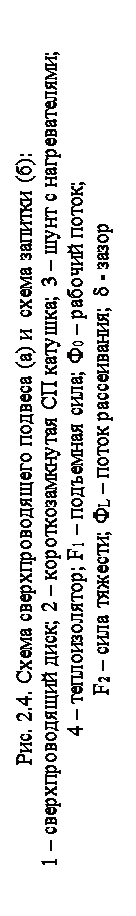        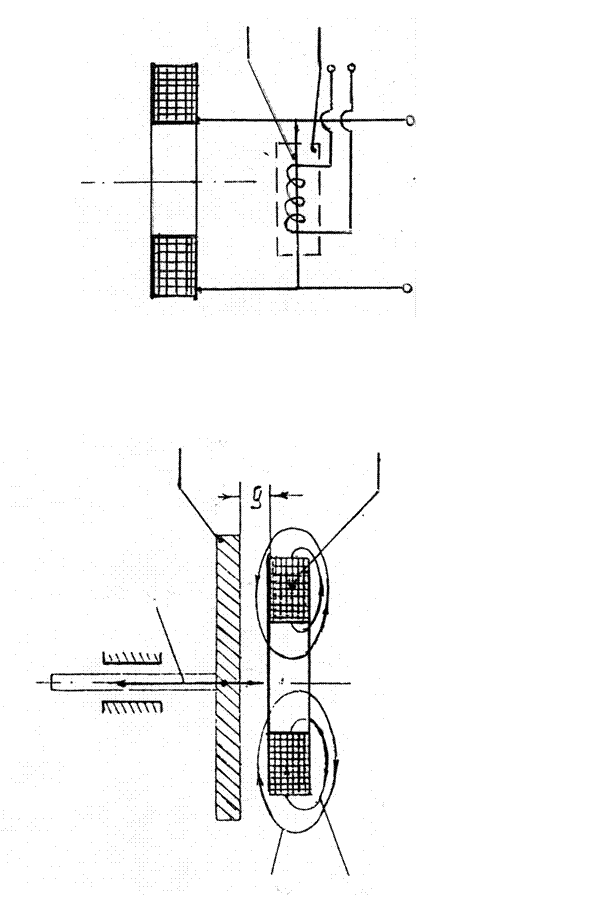 |
скают некоторой величины ток для того, чтобы повысить температуру шунта выше критической. Это устройство необходимо теплоизолировать, например пенопластом, т.к. оно погружено в жидкий гелий.
Кроме того, отметим, что обычно в левитирующем роторе возникают колебания, демпфировать которые можно, например, с помощью тонкого медного кольца, установленного под катушками подвеса.
Известен ряд конструкций сверхпроводящих гравиметров. Из них рассмотрим гравиметр Протеро и Гудкаинда [2.8], гравиметр Тумана [2.9], гравиметр Менде [2.10].
2.1.2.1. Гравиметр Протеро и Гудкаинда
На рис. 2.5 представлена схема сверхпроводящего гравиметра Протеро и Гудкаинда. В качестве чувствительного элемента (ЧЭ) в нем использована полая сфера диаметром 25,4 мм из алюминия, который при 4,2 К не является сверхпроводником (нормальное состояние), сверху сфера покрыта пленкой свинца толщиной 25 мкм (Тк = 7,2К). Суммарная ее масса ~ 5 гр. Для удержания сферы в бесконтактном состоянии использовались две короткозамкнутые сверхпроводящие катушки, расположенные вне корпуса ЧЭ. Каждая катушка имела диаметр 57 мм, наматывалась проводом из ниобия и содержала 400 витков. При эксплуатации через катушки пропускается постоянный ток такой величины, что индукция магнитного поля на поверхности сферы равнялась 218 Гc. Нижняя катушка 1 является удерживающей - она создает в подвесе силу, несколько превышающую 5г, а верхняя катушка 1 формирует градиент магнитного поля для ее центровки в аксиальном направлении. Напомним, что ось чувствительности гравиметра проходит вертикально через центр тяжести сферы. Такая система бесконтактной подвески ЧЭ является саморегулируемой: положение сферы в пространстве вдоль оси чувствительности определяется только ее весом, током запитки катушек, а также рабочей температурой, которая должна быть стабильной. После подъема сферы в рабочее положение катушку переводят в режим "замороженного потока". Это осуществляется при помощи сверхпроводящего шунта с нагревателем, после запитки катушек нагреватель выключают и тем самым шунтируют источник тока. Такие короткозамкнутые катушки бездиссипативны, в них транспортный ток не затухает сколь
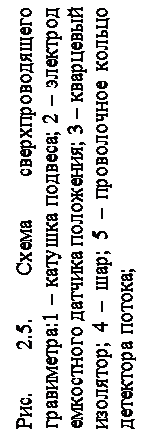
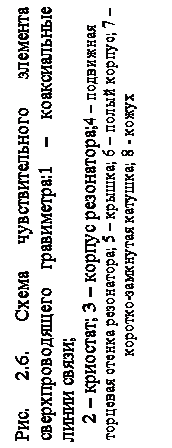
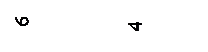
угодно долго, т.е. величина магнитного потока также не изменяется, поэтому любые изменения внешнего сигнала – силы тяжести (например увеличение) вызывают пропорциональные изменения положения ЧЭ (проседание), а, следовательно, увеличение индукции в зазоре и рост противодействующей (выталкивающей) силы. Произошедшие изменения пространственного положения ЧЭ измеряются шестью емкостными датчиками положения 2 (мостовая схема), а также изменением магнитного потока через кольцо 5 СКВИДа. Кольцо изготовлено из ниобия диаметром 15,7 мм и расположено под сферой.
Отметим некоторые конструктивные особенности гравиметра: катушки наматывались на массивный медный корпус 7, выточенный из одной заготовки, что исключает наличие сопротивлений потоку тепла и позволяет стабилизировать температуру по объему, где ее градиент в разных точках ничтожно мал, а точность поддержания 10-3К. В корпусе создан глубокий вакуум, что снижает теплообмен с окружающей средой и позволяет длительно работать при температуре жидкого гелия.
В процессе работы испытывалась катушка, намотанная проволокой из ниобия чистоты 99,98%. Однако в ней из - за плохой электроизоляции существовало межвитковое замыкание и это увеличивало температурный коэффициент электропроводности. Проволоки же из сплавов ниобия, включая многожильный кабель, не использовались из-за возникающего пиннинга вихрей. Измерения показали, что нестабильность величины тока не более 2 ∙10-7 в год.
Сложной оказалась регулировка тока в короткозамкнутых катушках с высокой точностью из-за температурных изменений при постоянно включенных тепловых ключах. В работе использовалась приближенная регулировка тока при открытых ключах (включен нагреватель ключа), затем при закрытом ключе слегка изменяли ток источника и подавали короткий импульс на нагреватель теплового ключа (шунта). Кроме того, нижняя катушка подключалась к своему источнику через трансформатор тока с отношением 106. Окончательная, тонкая регулировка проводилась изменением температуры до балансировки емкостного моста. Чувствительность этого гравиметра составляла 3 ∙10-8 м/с2, дрейф нуль -пункта не превышал 10-8 м/с2 в сутки. Даже эти параметры первого сверхпроводящего гравиметра соответствовали лучшим результатам обычных гравиметров.
2.1.2.2. Гравиметр Тумана
Автор в своей конструкции [2.9]. использует в качестве ЧЭ полную сферу с толщиной стенок 0,25 мм, изготовленную из ниобия. С целью вывешивания ротора используется сверхпроводящий магнитный подвес, который представляет собой короткозамкнутую катушку, намотанную ниобий - циркониевым проводом, и две градиентные катушки, расположенные параллельно. Они создают противоположно направленные магнитные поля с градиентом 1,45 эрс/см, предназначенные для устранения боковых биений ротора. Величина поля и его градиент регулируются током запитки обмоток катушек и поддерживаются постоянными. Экраны в виде цилиндров, выполненные из железо-никелевого сплава и сверхпроводящего из ниобия, защищают прибор от внешних магнитных полей и уменьшают эти поля до 10-9 Тл. Положение сферы в пространстве контролируется и измеряется сверхпроводящим квантовым магнитометром. Для этого над ЧЭ размещается катушка из сверхпроводника, между которой и сферой существует магнитный поток. При смещении ЧЭ, допустим вниз, зазор увеличивается и, следовательно, индукция поля в зазоре уменьшается. Магнитометр реагирует на эти изменения, возникает соответствующий сигнал, определяемый величиной смещения.
Теоретическая чувствительность предлагаемого прибора составляет 1,5 ∙ 10-13 м/с2 или ~1,5∙ 10-14g. Им можно измерять смещения гравитационной массы менее 10-10м или 1 Å. 


 .
.
2.1.2.3. Гравиметр Менде [2.10]
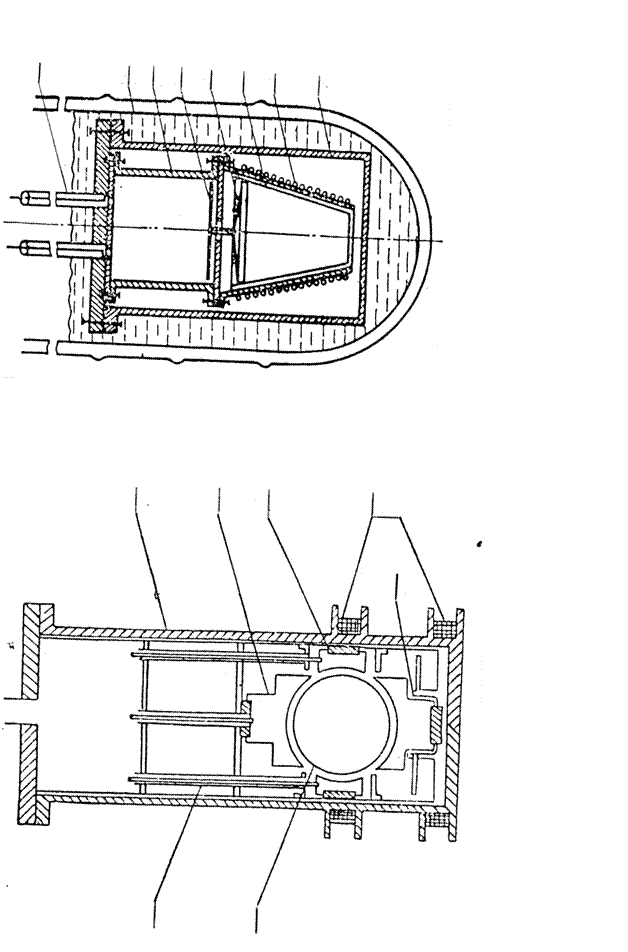
На рис. 2.6 представлена схема чувствительного элемента этого гравиметра. В качестве ЧЭ используется полый усеченный конус 6, который жестко соединен с крышкой 5 и подвижной торцевой стенкой резонатора 4. Эти элементы подвижной системы изготовлены из алюминия и покрыты пленкой свинца, что создает условия для левитации, т.к. при рабочей температуре гравиметра они переходят в сверхпроводящее состояние, т.е. обладают диамагнетизмом. Магнитное поле создается короткозамкнутым соленоидом 7, изготовленным из ниобий- титановой проволоки. Шунтирующий ключ, предназначенный для «захвата» магнитного потока в соленоиде, неразъемно соединен точечной сваркой.
В данном гравиметре в качестве детектора перемещений гравитационной массы (подвижной системы) используется сверхпроводящий, объемный резонатор СВЧ диапазона. В данной конструкции применен медный резонатор 3-см диапазона, внутренняя полость которого электролитически покрыта слоем свинца. Точность измерений величины смещения ЧЭ, а значит, и частоты колебаний зависит от добротности резонансной системы. В гравиметре добротность резонатора при температуре 4,2 К составляла 5 ∙106. Смещение стенки резонатора от положения равновесия, вызванное изменением силы тяжести, приводит к изменению длины резонатора, а, следовательно, его частоты, величина изменения которой и служит мерой измеряемой вариации силы тяжести. Вся конструкция - гравитационная масса и резонатор помещается в герметизированный кожух 8, в котором создается вакуум, и погружается в ванну с жидким гелием криостата 2.
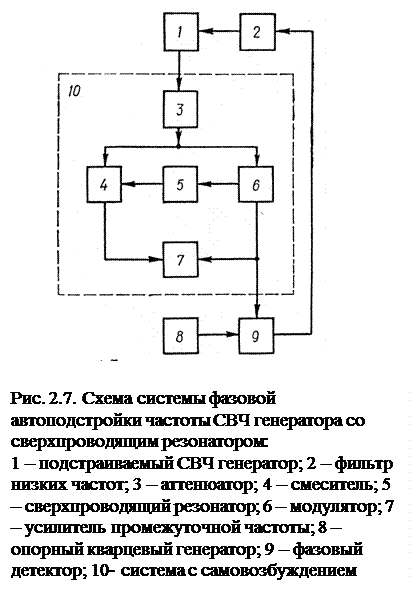 После охлаждения чувствительного элемента в целом производят запитку соленоида. Вследствие того, что подвижный элемент в виде усеченного конуса и его соленоид осесимметричны, это не только существенно упрощает центровку ЧЭ относительно оси чувствительности, но и не требует, как в предыдущих конструкциях, дополнительных управляющих катушек. Полый конус при некотором значении транспортного тока в соленоиде начинает левитировать при условии равенства выталкивающей силы и веса всей подвижной системы. При увеличении тока запитки последняя перемещается вверх – увеличивается зазор между конусом и соленоидом до тех пор, пока автоматически не восстановится равенство сил. Так устанавливается начальное положение ЧЭ гравиметра. После этого соленоид с помощью теплового ключа переводится в режим "замороженного потока".
После охлаждения чувствительного элемента в целом производят запитку соленоида. Вследствие того, что подвижный элемент в виде усеченного конуса и его соленоид осесимметричны, это не только существенно упрощает центровку ЧЭ относительно оси чувствительности, но и не требует, как в предыдущих конструкциях, дополнительных управляющих катушек. Полый конус при некотором значении транспортного тока в соленоиде начинает левитировать при условии равенства выталкивающей силы и веса всей подвижной системы. При увеличении тока запитки последняя перемещается вверх – увеличивается зазор между конусом и соленоидом до тех пор, пока автоматически не восстановится равенство сил. Так устанавливается начальное положение ЧЭ гравиметра. После этого соленоид с помощью теплового ключа переводится в режим "замороженного потока".
Резонансная частота и ее изменения измеряются с помощью устройства, структурная схема которого представлена на рис. 2.7. Сигнал с частотой Ω (ωr) подается на фазовый детектор 9, куда поступает также сигнал от радиочастотного кварцевого генератора 8 с частотой Ωо. С выхода фазового детектора сигнал ошибки через фильтр низких частот 2 подается на СВЧ генератор 1. Далее он через аттенюатр 3 подается на смеситель 4, на вход которого включен сигнал со сверхпроводящего резонатора 5. Относительная нестабильность частоты СВЧ генератора, обусловленная нестабильностью Ωо, будет в 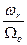 раз меньше относительной нестабильности частоты кварцевого генератора. Это отношение составляет 103-104.
раз меньше относительной нестабильности частоты кварцевого генератора. Это отношение составляет 103-104.
Такой гравиметр при бездрейфовом подвесе имеет чувствительность порядка 10-10g при усреднении частоты выходного сигнала за 1 сутки 10-9 g. Чувствительность измерений гравиметра может быть повышена примерно на два порядка за счет уменьшения градиента магнитного потока.
Перспективность предлагаемого метода измерения линейных перемещений подтверждается имеющимися разработками, например в дилатометрии, где удалось добиться чувствительности 10-14м или 10-4 Å, а также то, что выходной сигнал несет информацию об измеряемой величине в виде частоты электромагнитных колебаний, а обработка такого сигнала не представляет трудностей.
2.1.2.4. Равножесткий гравиметр
Рассмотрим еще один вариант гравиметра, в котором чувствительный элемент в виде пустотелой сферы бесконтактно вывешен в пространстве [2.18]. В отличие от уже рассмотренного [2.8] и других существующих конструкций в этом гравиметре используется шесть сверхпроводящих электромагнитных полюсов, которые имеют одинаковую жесткость по трем осям координат. Конструктивно корпус гравиметра (рис. 2.9) представляет собой куб размерами 70 х 70 мм, выполненный из слитка ниобия высокой чистоты. На каждой грани в ее геометрическом центре высверлены сквозные отверстия
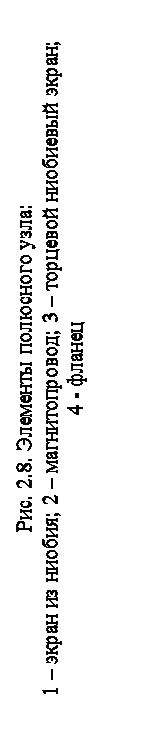   |


 а a
а a
B2 r q2 C
q1
r1 0¢
r0
B1 r2 1
h
Фк 3
Ф3 4
2r3
2r1
б
Фк
Ф3
Фn
Rmn
Em Rn
R3
|
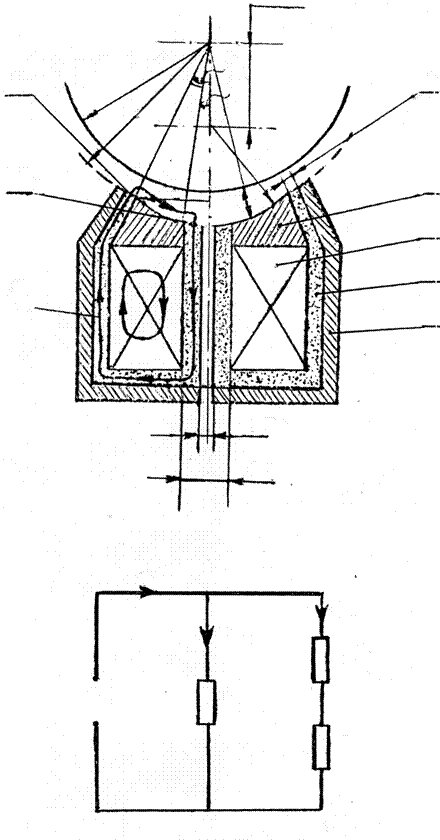
диаметром 40 мм строго по осям симметрии. Наиболее ответственными элементами являются шесть однотипных узлов подвеса – полюсов (рис.2.8), схема конструкции которых показана на рис. 2.10, а. Катушка 2 намотана бифилярно сверхпроводящим проводом диаметром 0,3 мм и содержит 500 витков. Каждая из них размещается под полюсным наконечником 1 из ниобия в промежуточной гильзе 3 из магнитомягкого материала, по которому замыкается магнитный поток. Полученный блок плотно вставляется в экран 4 из ниобия. В этой конструкции в качестве инерционного тела используется пустотелая сфера из титана, на которую нанесен слой ниобия толщиной 5 мкм. Этот слой должен обладать сплошностью, равномерной толщиной так, чтобы после его нанесения геометрический центр симметрии также совпадал с центром масс сферы.
Для того чтобы обеспечить (при запуске) подъемную силу, близкую к расчетной, необходимо иметь вкладываемые поверхности подвижного тела и полюсных наконечников разнопрофильными. Из проведенного анализа [2.19] и расчета аналитически был получен довольно сложный профиль сечения полюса: он должен иметь форму, близкую к поверхности эллипсоида вращения. Для того чтобы изготовить необходимый профиль поверхности полюса, требовалось сложное технологическое оборудование, поэтому в разработке несколько упростили конструкцию: изготовили вогнутую поверхность в виде сферы радиусом, несколько меньшим, чем радиус шара rц< r1 (рис. 2.10, а), и его геометрический центр сдвинут от точки 0 до 01 на величину а. Это позволило в некоторой степени достичь постоянства модуля напряженности магнитного поля на поверхности инерционного тела и тем самым создать необходимую начальную подъемную силу. Из рисунка видно, что после запитки катушек транспортным током созданный магнитный поток имеет составляющую Фк и основной поток Ф3, который проходит по магнитопроводу 3 в рабочем зазоре между сферой (телом подвеса) и полюсными наконечниками. Индукция в нем изменяется от В1 до В2 в различных точках рабочей поверхности, создается выталкивающая сила, превышающая вес инерционного тела. Реальная конструкция сборного узла электромагнитного полюса поэлементно показана на фотографии (рис. 2.9).
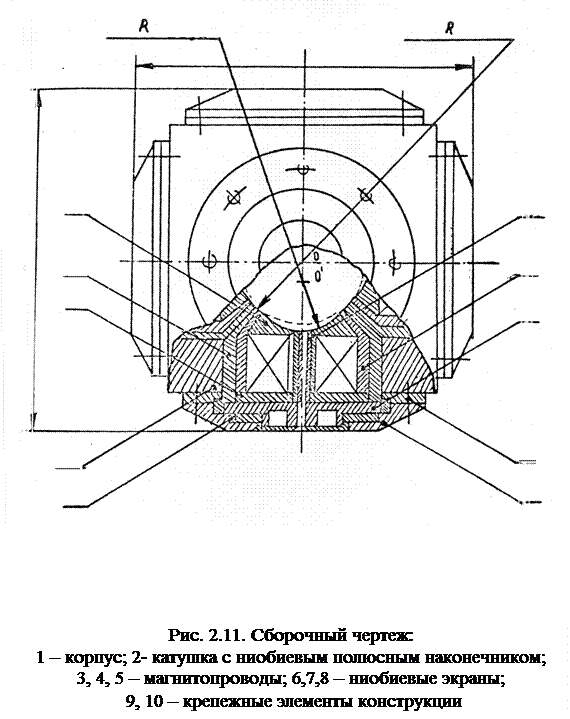
В целом конструкция датчика гравиметра с равножестким подвесом показана на рис. 2.11. Все шесть электромагнитных полюсов установлены в корпусе 1 и по очереди юстированы в необходимом положении. В качестве преобразователей положения инерционной
15,1
76*
2 5
| 76* |
8 3
4 6
1 9
10
2 5
массы в процессе предварительных исследований использовали индуктивности. Они вклеивались в осевые отверстия полюсов и представляли катушки, намотанные медным проводом на цилиндрический каркас диаметром 20 мм. Обмотка катушек содержала 300 витков провода марки ПЭВ диаметром 0,08 мм. Собственная их индуктивность составляла 100 мкГн. Необходимо отметить, что полюсные катушки запитывались от внешнего источника после того, как в криостат, где находился ЧЭ гравиметра, заливался жидкий гелий и температура достигала 4,2 К. В рабочем объеме, где располагался ЧЭ, создавалось разрежение на уровне 10-3 Тор с помощью адсорбционных насосов. После откачки перекрывали вентиль, и в процессе испытаний вакуум не ухудшался. Когда инерционное тело занимало рабочее положение, т.е. бесконтактно вывешивалось в центре объема прибора, катушки полюсов переводились в режим "замороженного потока" с помощью тепловых ключей. Сами тепловые ключи устанавливались снаружи на крепежных элементах полюсов и имели конструкцию, описанную в разделе 2.2.1.4.
Для данной конструкции рассчитаны параметры подвеса. Они оказались следующими:
1) геометрические параметры Sin θ2 = 0,6; Sin θ1= 0,16; в = r – ro = 1,7 мм ; а ≤ 2,3 (рис. 2.10, а);
2) жесткость подвеса С = 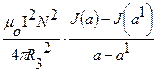 , при Rк = 0, Rmn= 0, I = 0,64 А, N = 500 витков, а = 2,3 , а1= 2,25 имеем С = 17690 Н/м;
, при Rк = 0, Rmn= 0, I = 0,64 А, N = 500 витков, а = 2,3 , а1= 2,25 имеем С = 17690 Н/м;
3) собственная частота подвеса f = 250 Гц и С = 17690 Н/м подтверждается массой подвижного тела m ≤ 7,2 10-3кг из неравенства m< 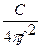 ;
;
4) подъемная сила F= 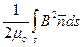 , где
, где 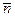 – единичный вектор в направлении силы тяжести, ds – элемент поверхности инерциального тела, F = 0,29Н при I = 0,64 А; число витков N = 500; Rмn= 0, а = 2,3 (рис. 2.10, б);Чувствительность гравиметра составляет 8,69 ∙ 10-12g при Т = 4,2 К, ∆f = 50 Гц, r = 15мм, m = 7,2 ∙10-3кг.
– единичный вектор в направлении силы тяжести, ds – элемент поверхности инерциального тела, F = 0,29Н при I = 0,64 А; число витков N = 500; Rмn= 0, а = 2,3 (рис. 2.10, б);Чувствительность гравиметра составляет 8,69 ∙ 10-12g при Т = 4,2 К, ∆f = 50 Гц, r = 15мм, m = 7,2 ∙10-3кг.
2.2. Акселерометры
Слово акселерометр происходит от латинского Ассеlero – ускоряю и греческого metreo - измеряю, т.е. это прибор для измерения ус-
 1 2 3 4 5
1 2 3 4 5
 |
 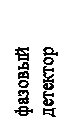 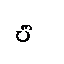 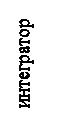 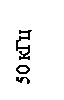     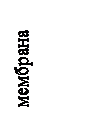    |
корений (перегрузок) или торможений в транспортных машинах, летательных аппаратах и т.п.
Отметим, что если в гравиметрах ось чувствительности направлена перпендикулярно горизонтальной поверхности, в акселерометрах она в основном направлена параллельно ей, т.е. лежит в горизонтальной плоскости.
В существующих сверхпроводящих акселерометрах, как и в гравиметрах, имеющих перемещающиеся и вращающиеся узлы, повышение чувствительности и точности связано, прежде всего, с применением опор, приближающихся по своим свойствам к идеальным. Наиболее полно свойствам идеальной опоры отвечают подвешивающие системы, в которых подвижные тела остаются без контакта с корпусом. Этого можно достичь в земных условиях за счет магнитных и электростатических сил, а также потока газа, которые компенсируют силы гравитации. Это состояние левитации получают при использовании электромагнитных, электростатических и некоторых других подвесов. Однако в некоторых криогенных приборах используются слабосвязанные, упругие подвесы, но их приближение к идеальным подвесам определяется добротностью подвеса, а значит, материалом упругого подвеса, соотношением массы подвижного элемента и массы корпуса и параметрами окружающей среды, чему будет уделяться особое внимание.
Сверхпроводящие акселерометры, подвижные элементы (ПЭ) которых по способу установки в корпусе делятся на:
- контактные, в которых ПЭ связан с корпусом;
- неконтактные, где ПЭ левитирует.
В данной работе рассмотрим сверхпроводящие акселерометры, ПЭ которых выполнены в виде мембраны [2.11], консоли (язычка) [2.12,2.16,2.17] или закреплены на пружинах [2.13], а также шпули висящей в пространстве [2.14] и сверхпроводящей сферы [2.15] с бесконтактным подвесом.
2.2.1. Акселерометры с контактным типом подвеса ЧЭ
2.2.1.1. Акселерометр Пэйка [2.11]
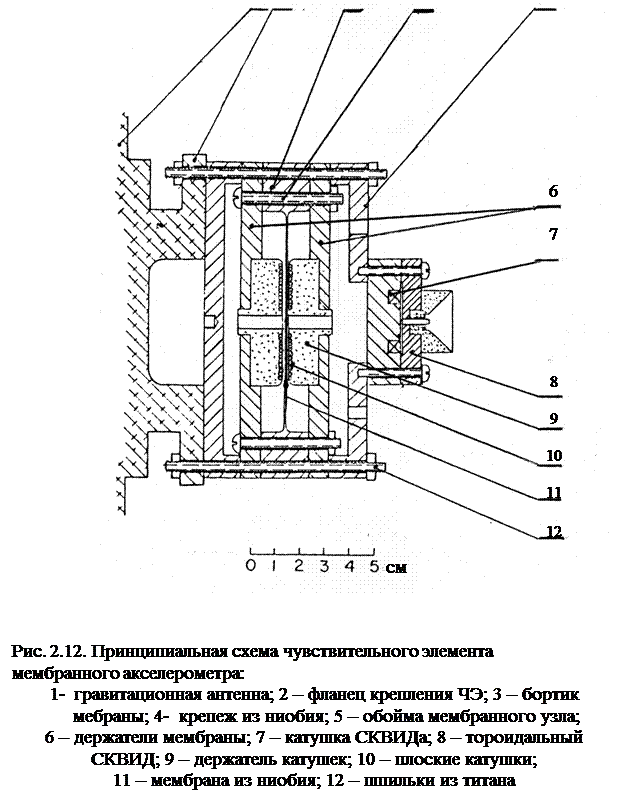
Схема ЧЭ показана на рис. 2.12. В этой конструкции подвижным элементом, воспринимающим полезный сигнал, служит мембрана 11 из ниобия чистоты 99,9%, которая изготовлена из диска путем механической его обработки с обеих боковых плоскостей и последующего электрохимического травления до толщины мембраны 0,1 – 1 мм. Она имеет форму окружности, и ее окружает утолщенный бортик 3 (как видно из рисунка), масса которого существенно больше массы самой мембраны, для того чтобы не было перекачки энергии колеблющейся подвижной массы в корпус. Мембрана плотно зажимается держателями 6 с помощью винтов из ниобия.
Мембрана с держателями и корпусом называемые обойма или мембранный узел, устанавливается на объекте – гравитационной антенне, воспринимает полезный сигнал и испытывает ускорение под его воздействием. В данной работе для определения ускорения гравитационной антенны (алюминиевая балка) преобразователем смещения служат две плоские сверхпроводящие катушки 10, расположенные по обе стороны мембраны. Катушки выполнены из провода сплава ниобий-титан диаметром 50 мкм в виде спирали Архимеда. Такие катушки крепятся в держателях 9. Они состоят из двух частей: стекло - эпоксидной с выточкой под катушку и пластинки, которые между собой после установки катушки соединяются низкотемпературной эпоксидной смолой и тремя винтами из ниобия (на рисунке не показаны). Через эти диэлектрические держатели проникает магнитное поле, а там, где используется ниобий, поле экранируется. Так обойма 6 выполнена из ниобия и защищает внутреннюю полость ЧЭ от внешних магнитных полей. В этой связи контакты тепловых ключей, необходимые для преобразования постоянных токов катушек, вынесены на внешние поверхности держателей.
Для измерения изменений магнитного потока в зазоре между мембраной и катушками, а значит, величины смещения мембраны используется тороидальный СКВИД 8, закрепленный на обойме мембранного узла. СКВИД изготовлен из ниобия и имеет слабую связь (точечный контакт). В виде тора выполнена спираль 7 из проволоки ниобия, имеющая до 80 витков, и она уложена в проточку корпуса СКВИДа.
Две плоские катушки L1 и L2 (см. рис. 2.13) образуют сверхпроводящий контур, по которому циркулирует постоянный ток Iо параллельно включенный катушке L3 в ней так<
| <== предыдущая лекция | | | следующая лекция ==> |
| НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ЭФФЕКТЫ В СВЕРХПРОВОДНИКАХ | | |
Дата добавления: 2020-03-21; просмотров: 911;











