НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ЭФФЕКТЫ В СВЕРХПРОВОДНИКАХ

Ранее нами были рассмотрены физические основы сверхпроводимости: отсутствие сопротивления протеканию тока и идеальный диамагнетизм, проникновение магнитного потока в сверхпроводники и барьер Бина - Ливингстона, пиннинг и движение вихрей, квантование магнитного потока и эффекты Джозефсона, которые имеют место в рассматриваемых ниже низкотемпературных приборах и устройствах.

Однако существуют и другие менее известные физические явления в сверхпроводниках, но которые оказывают существенное влияние: одни на чувствительность, надежность и долговременную стабильность приборов, другие на работоспособность и силовые характеристики устройств и механизмов. Здесь мы рассмотрим поглощение низкочастотного звука в сверхпроводящем состоянии; потери, определяемые наведенным переменным магнитным полем; роль упругого барьера, проникновению магнитного поля в объем сверхпроводника; влияние движения магнитного потока, вызванное вращением сверхпроводника, и процессы его релаксации.

Прежде чем переходить к рассмотрению каждого из этих физических процессов, изученных экспериментально на классических сверхпроводниках и теоретически обоснованных, проведем анализ существующих ситуаций на примере ряда низкотемпературных устройств, которые нами будут рассмотрены в последующих главах. Начнем с акселерометров, гравиметров и градиентометров с контактным типом подвеса пробного тела [2.11; 2.12; 2.16; 2.17] (разделы 2.2.1, 2.2.1.2, 2.2.1.3, 2.2.1.4) и с неконтактным типом подвеса [2.8 – 2.10; 2.14; 2.15 и 2.18] (разделы 2.1.2.1.-2.1.2.4., а также 2.2.2.1 и 2.2.2.2).

В приборах первого типа чувствительный элемент в виде мембраны, консоли или струны (он же подвижное тело), как правило, изготавливается из ниобия, охлаждается до температуры 2 – 4,2 К и под действием полезного сигнала изменяет свое положение в пространстве на пропорциональную величину, может совершать колебания на собственной частоте 10² ÷ 10⁴ Гц обычно в вакууме. Для того чтобы исключить влияние внешнего магнитного поля его, например, экранируют. Добротность ЧЭ (Q) этих приборов составляет 10⁵ ~ 10⁶, т.е. величина внутреннего трения Q^-1 материала ЧЭ составляет 10^-5 ÷10^-6. В таких приборах не следует допускать появления дополнительных потерь энергии в диапазоне температур 2 ÷ 10 К.

В приборах другого типа ЧЭ в виде сферы обычно полой, усеченного конуса, шпули или другой формы, выполняются также из ниобия, вывешиваются в пространстве во внешнем магнитном поле за счет их диамагнетизма; они охлаждаются до температуры жидкого гелия, имеют собственную частоту колебаний ~ 800 Гц (например [2.14]), добротность ~ 10⁶, внешние магнитные поля ~ 200 ÷ 300 Гс (например [2.8]). Таким образом, в этих условиях возможно возникновение переменного магнитного поля на поверхности сверхпроводника, совершающего периодические движения, как будет показано в этой главе, а также проявление упругого поверхностного барьера проникновению магнитного поля в объем сверхпроводящего ЧЭ (с чем будем также знакомиться). Величина упругого поверхностного барьера препятствующего входу и выходу вихрей внешнего магнитного поля при изменении последнего в объеме сверхпроводника, как показали экспериментальные исследования, является управляемым параметром. Она определяется реальной кристаллической структурой приповерхностного слоя, которую можно изменять механическим и термическим воздействием, химической или электрохимической обработкой, а также другими технологическими приемами (например, напылением слоя покрытия).

Далее в различных по конструкции охлаждаемых электромагнитных опорах (подвесах, подшипниках, левитирующих устройствах), которые составляют основные элементы конструкции охлаждаемых микро-, малой и средней мощности электромашин (рассматриваются в главе 3) и ряде навигационных приборов (глава 2), магнитный поток формируется в пространстве между катушкой, создающей это поле, и левитируемым телом, которое изготовлено из сверхпроводника и выполняет роль электромагнитного экрана. В этом пространстве возникает магнитное поле с индукцией Ве ≤ Вк₁. В зависимости от величины упругого барьера сверхпроводящего экрана [1.14] величина индукции, при прочих равных условиях, может изменяться: при малом по величине барьере она уменьшается, а следовательно, уменьшается и выталкивающая (противодействующая) сила, удерживающая в неконтактном положении это левитирующее тело, или наоборот. В ряде экспериментальных исследований было обнаружено выталкивание вихрей из объема тела при его вращении, что существенно увеличивает величину индукции поля в зазоре, а значит, и противодействующую силу, т.е. при этом улучшаются силовые характеристики опор [1.16]. Изменяя силу пиннинга вихрей, можно, таким образом, управлять эффективностью работы опор этих устройств и приборов.

На основании проведенного анализа установим основные параметры и пределы их изменения, характеризующие работу низкотемпературных устройств и приборов, в которых используются сверхпроводящие элементы, а также основной конструкционный материал чувствительного элемента:

- температура 2 ÷ 10 К;

- рабочая частота 10² ÷ 10³ Гц;

- магнитные поля ~ 0 ÷ 10³ Гс;

- добротность 10⁵ ÷ 10⁶;

- вакуум 10^-1 ÷ 1^-5 Тор;

- конструкционные материалы – ниобий и его сплавы.

1.1. Основной метод исследования

Мы отмечали, что в реальных условиях эксплуатации рассматриваемых устройств на сверхпроводник действует ряд факторов. К ним относятся температура, магнитное поле (постоянное и переменное), гравитационное поле, колебания звуковой частоты с малой амплитудой. Изменения этих параметров сопровождаются флуктуационными процессами. В этой связи выбор основного метода исследований имеет решающее значение. Был выбран метод внутреннего трения [1.1], который позволяет проводить исследования в звуковом диапазоне частот (10 ÷ 10⁴ Гц) [1.2-1.4; 1,9; 1.7 и др.] температурах жидкого гелия (2 -10 К), присутствии магнитного поля (до 1 кГс) на образцах в виде пластинки, стержня, мембраны, т.е. требуемых внешних условиях и объектах, близких по форме к элементам конструкций приборов. Последующая модификация метода, как будет показано ниже, расширила [1.12 -1.14; 1.16] область исследования и позволила изучать магнитомеханические эффекты в сверхпроводниках в тех же условиях, обнаружить упругий барьер проникновению магнитного поля. Прежде чем переходить к обсуждению результатов исследований, отметим, что методом внутреннего трения обычно измеряют величину затухания колебаний образца (ВТ, Q^-1) на собственной частоте (как правило, в амплитудо - независимой области) в зависимости от температуры. При этом управляемыми параметрами являются такие, как частота колебаний, реальная кристаллическая структура объекта и некоторые другие. Далее в главе будут встречаться зависимости Q^-1(Н), но это будет уже не внутреннее трение, а некоторый параметр, обозначающий затухание от внешнего магнитного поля, и этот выбранный параметр обозначен как δ (мог быть Г, ΔW и т.д.), но не Q^-1 и не логарифмический декремент затухания [1.1].

Известно, что наиболее употребляемой характеристикой внутреннего трения является величина

Ψ = 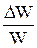, (1.1)

где ΔW – энергия, рассеянная за период по всему объему образца, W – энергия колебаний всего образца.

Величину Ψ называют коэффициентом поглощения. Есть еще одна величина – добротность Q, которая связана с коэффициентом поглощения соотношением

Q = 2 π/ Ψ. (1.2)

Внутренним трением считается величина, обратная добротности, т.е. Q^-1. Для определения величины внутреннего трения можно использовать

Q^-1 = 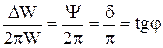, (1.3)

где φ – угол сдвига фазы между напряжением и деформацией, tg φ – тангенс угла потерь, δ – логарифмический декремент затухания колебаний, Ψ = 2 δ.

В случае слабого затухания колебаний образца (высокая добротность) для определения величины внутреннего трения использует следующее выражение:

Q^-1 = 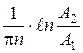, (1.4)

где n – число колебаний образца между выбранными значениями их амплитуд А₁ и А₂.

По измеренной величине внутреннего трения (1.4) и частоте колебаний f можно оценить ряд параметров материала: модуль Юнга, энергию активации, амплитуду колебаний. Для образца в виде пластинки модуль Юнга можно определить по выражениям

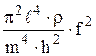Е = или Е = 48 , (1.5)

где ρ – плотность материала образца, его длина - ℓ, толщина – h, коэффициент Пуассона ν, частота колебаний f, масса - m .

Энергию активации

Н = 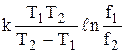, (1.6)

где k – постоянная Больцмана, Т₁ и Т₂ – температуры максимумов Q^-1, соответствующие частотам f₁ и f₂.

Амплитуду колебаний (стрелка прогиба)

Δх_m= 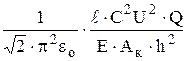, (1.7)

где С – емкость конденсатора раскачки образца, А_к – площадь обкладки конденсатора, U – напряжение на конденсаторе, ε_о = 8,854 ·10^-12 .

1.2. Потери энергии в сверхпроводящем состоянии

В 60 – 70^х годах прошлого столетия было обнаружено аномальное по характеру поглощение низкочастотного звука в области температур 2 ÷ 5 К на частотах 80 кГц [1.2] и ~ 2 кГц [1.3] в ниобии. На рис. 1.1 и 1.2 это показано в соответствии с экспериментальными исследованиями в виде зависимостей Q^-1(T).

Физическую ситуацию рассмотрим на примере экспериментальных исследований [1.3,1.4]. Образец совершает колебания на собственной частоте, и добротность такой колебательной системы (образец, зажим (держатель) образца) определяется только внутренними источниками потерь, если остальные источники такие как внешняя среда, перекачка энергии и другие устранены [1.5, 1.6], то при

наличии таких источников добротность системы уменьшается, т.е. растет ВТ, и это в экспериментальных исследованиях проявляется в виде пика на кривой Q^-1(T) некоторой «протяженности» по температуре, пока действует источник потерь. Как правило, простые пики имеют малую протяженность, т.е. на графиках они узки, и, как в рассматриваемом случае, составляют у основания 0,2 К (рис. 1.2). Таким образом, этот пик ВТ соответствует сверхпроводящему состоянию ниобия.

В экспериментальных исследованиях показано, что максимум на температурной зависимости затухания колебаний сверхпроводника существует независимо от их частоты, а величина температуры его проявления определяется только частотой при прочих равных условиях: чем выше частота, тем ниже температура, при которой наблюдаются эти дополнительные потери (рис.1.3). Известно, что вклад во внутреннее трение вносят разные факторы: тепловая релаксация Зинера, фононы, электроны проводимости, дефекты кристаллической решетки. Расчеты осуществляют по формулам [1.1] для электронной составляющей вклада

Q_эл = 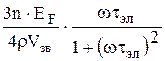(1.8)

и фононной

Q_ф = 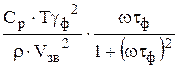, (1.9)

где n – число электронов в металле, n ~ 10²⁹ м^-3, Е_F - энергия Ферми, Е_F~ 5 ·10^-19Дж; ρ_Nb – плотность ниобия, ρ_Nb = 10 Т· м^-3; V_зв – скорость звука, V_зв ~ 10³ м/с; С_р - удельная теплоемкость С_р ~ 2 ·10^-3 Дж· Г^-1· К^-1; γ_ф ~ 2; τ_эл – время релаксации электронной составляющей, τ_эл ~ 10^-12 ÷ 10 ^-14 с; τ_ф ~ 10^-10с; ω – частота колебаний, ω~10³.

Подставив эти значения в выражения (1.8) и (1.9), получим численные значения вкладов Q_эл^-1 ~ 10^-9 и Q_ф^-1 ~ 10^-12. Они по своей величине экспериментально не определимы также как и тепловая релаксация Зинера. Таким образом, ясно, что только дефекты кристаллической решетки могли быть ответственны за наблюдаемые особенности ВТ. Основное влияние на величину потерь оказывали плотность дислокаций и примеси. Из исследований [1.2 и 1.4] следует, что у недеформированного монокристалла (плотность дислокаций которого составляла 10⁶см^-2) потери небольшие (кривая 2 рис.1.2 и 1.1). Если же эти монокристаллы деформировать, например двухсторонним обжатием, на 15 % [1.4], плотность дислокаций возрастает до N ~ 10⁹см^-2 и это вызывает рост потерь, как видно на рис. 1.2 (кривая 1), пик Q^-1 на частоте 1370 Гц заметно возрастает также, как и в серии экспериментов [1.2] (рис.1.1), где частота составляла 80 кГц.

В другой серии экспериментальных исследований [1.4] использовались образцы из ниобия, отличающиеся числом примесей, которые составляли 9·10^-5, 2 ·10^-4 и 2 ·10^-3 при равной плотности дислокаций и частоте колебаний ~ 1700 Гц. Оказалось, что, чем чище сверхпроводник, т.е. меньше примесей, тем больше затухание, т.е. больше пик, а значит, и величина потерь (кривая 1, рис.1.4). Если например, число примесей возросло почти на 2 порядка, то потери снизились в 5 раз (сравните по величине пики на кривых 3 и 1).

Таким образом, из этих экспериментов следовало, что в ниобии в области температур 2 – 5 К на зависимости ВТ от частоты звуковой волны (1 ÷ 80 кГц) наблюдается дополнительное рассеяние энергии, аномальное по характеру, которое связывается с реальной кристаллической структурой сверхпроводника.

Наибольший статический вес среди дефектов имеют дислокации, которые вносят вклад во внутреннее трение из-за двух основных диссипативных процессов: динамических потерь и релаксации. В диапазоне звуковых частот динамические потери очень малы и поэтому ВТ обусловлено только релаксационными процессами. Эти процессы связаны с образованием перегибов на дислокациях и преодоления ими центров закрепления. Движение перегибов осуществляется под действием внешних напряжений, термических и квантовых флуктуаций. При измерении ВТ в амплитудонезависимой области внешние напряжения столь малы, что основную роль в процессе открепления дислокаций играют квантовые флуктуации.

Для амплитудонезависимого ВТ, связанного с релаксационными процессами в модели Зинера, можно записать выражение [1.1].

Q^-1 = Δ_{м 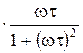,} (1.10)

где Δ_м – максимальное значение дефекта модуля, τ – время релаксации.

Из условия ωτ =1 найдем наибольшее значение ВТ

Q^-1_{макс =} 0,5 · Δ_м.

На основании модели амплитудонезависимого релаксационного внутреннего трения в линейном по напряжению приближении величина ВТ определяется выражением

Q^-1 = . (1.11)

Откуда следует, что амплитудонезависимая часть ВТ имеет максимум Q^-1_макс = 0,126 Δ_м при ωτ = 1,33. Форма пика Q^-1 (ωτ) ассиметрична относительно оси, проходящей через максимум. Эти выражения (1.10) и (1.11), как показано в работе [1.7], можно модифицировать в случае сверхпроводника, находящегося при температуре ниже критической, если для τ = ω^-1 (Т) использовать выражение

ω = v (Т) еxp 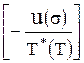, (1.12)

где v (Т) – эффективная частота, u (σ) – энергия активации, Т^*(Т) – эффективная температура.

При этом необходимо учитывать, что в области сверхпроводящего перехода происходит изменение v (Т) из-за уменьшения коэффициента торможения дислокаций электронами проводимости. Полученная температурная зависимость ω в графическом варианте показана на рис. 1.5, которая позволяет определить особенности ВТ в области Т < Т_к. Из [1.7] известно, что это изменение существенно для больших длин колеблющихся дислокационных сегментов (ℓ > ℓ_o ~ 10^-6м). Если же ℓ << ℓ_o, то при сверхпроводящем переходе v (Т) практически не меняется.

Отметим, что изменения v (Т) наиболее существенны в случае больших длин дислокационных сегментов (ℓ > ℓ_o = 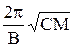), где С = 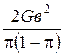- линейное натяжение дислокации, ℓ - длина дислокационного сегмента, В – коэффициент вязкого торможения дислокаций, М = πв²ρ - эффективная масса единицы длины дислокации.

Из рис. 1.5 (нижняя кривая) видно, что в этом случае в интервале частот от ω₁ до ω₂ должен существовать пик Р₂ с вершиной, соответствующей температуре Т₂, если образец колеблется с частотой ω₁ . При увеличении частоты до ω₂ пик должен сдвинуться в сторону меньших температур (до Т₃). Из этой модели следовало, что пик ВТ должен наблюдаться только на чистых сверхпроводниках с небольшой плотностью дислокаций.

Для сравнения предсказаний этой теоретической модели с экспериментальными результатами воспользуемся данными, приведенными на рис. 1.4. Увеличение концентрации примесей приводило к уменьшению высоты пика. Исходя из процентной концентрации примесей, оценим среднее расстояние между примесями, которое определяет среднюю длину дислокационного сегмента, приняв

ℓ~ 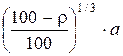, (1.13)

где ρ – процентная чистота материала, а – постоянная кристаллической решетки.

Из формулы (1.13) для ниобия чистоты 99,991 % и а = 3,3 ·10^-10м определим среднюю длину дислокационного сегмента ℓ≈ 7· 10^-8м, выясним величины параметров, которые определяют частоту попыток отрыва дислокации (уравнение (1.12)) для рассматриваемых экспериментальных данных [1.3, 1.4]. Полагая ℓ ~ 7· 10^-8м, а = в = 3,3 10^-10м, В ~ 10^-5 Н ·с · м², v = 0,375, G = 7,7· 10¹⁰ Н· м^-2 , получим значение собственной частоты дислокационного сегмента ω_е ~ 7,7 ·10¹⁰ рад· с^-1, коэффициент демпфирования γ = 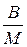= 3,7 ·10⁹ с^-1 и характеристическую температуру θ ~ 62 К. В рассматриваемом сверхпроводнике имеем ω_е > γ, поэтому влиянием демпфирования дислокации можно пренебречь и тогда v (Т) = ω_е.

Как и в работе [1.7], используем модель Коявы – Хасигути, согласно которой при условии << 1 из выражения (1.11) следует

Q^-1 = 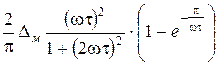. (1.14)

Кроме этого, выбор модели [1.7] обусловлен тем, что из экспериментальных данных видна их близость к условию Q^-1_макс = 0,126 Δ_м, чем к условию Q^-1_макс = 0,5 Δ_м. С увеличением частоты колебаний образца пики сдвигаются в область более низких температур (рис.1.3).

Таким образом, в рамках этой модели нашли объяснение основные результаты проведенных здесь экспериментальных исследований. Кроме того, на ее основе теперь можно определить ряд параметров сверхпроводников, например, энергию взаимодействия дислокации с примесью Е_n = 2·10³ К, изменение энергии электростатического их взаимодействия при сверхпроводящем переходе, которая оказалась равной ΔЕ_n-s(0) = -1 К и некоторые другие.

1.3. Потери энергии в области N – S перехода

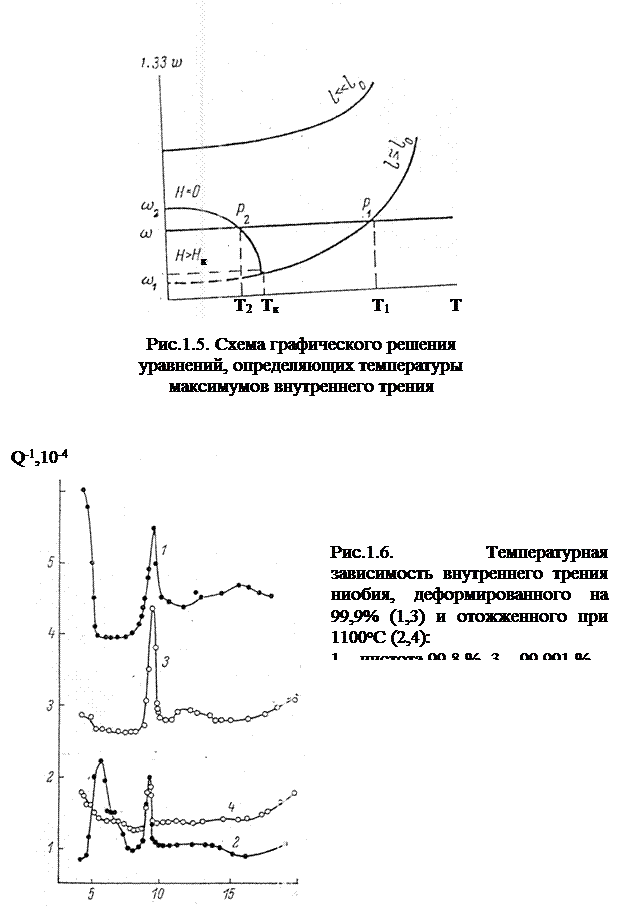
Исследования в области гелиевых температур на низких частотах, которые являются наиболее перспективными с точки зрения практического использования, проводилось методами составного вибратора (например [1.2]), изгибных [1.7] и крутильных [1.11, 1.12] колебаний. Были обнаружены особенности в затухании звука при сверхпроводящем переходе. Основные исследования проведены на ниобии и его сплавах, а также на модельных сверхпроводниках (свинец и сплавы на его основе). Выявлено (например, [1.2, 1.8, 1.12], что фон ВТ в сверхпроводящем состоянии ниже, чем в нормальном. Однако наибольший интерес представляют результаты исследований [1.8, 1.4 и 1.10], где в области сверхпроводящего перехода обнаружен четко выраженный пик Q^-1(Т) (см. рис.1.6). Этот пик всегда и на всех сверхпроводящих материалах приходится на Т_к, имеет ширину по оси температур в пределах 0,05 – 0,8 К, как видно из рис. 1.6, а по высоте он превышает фон внутреннего трения в 2 и более раз (иногда более чем на порядок). Разрушение сверхпроводимости магнитным полем в тех же температурных условиях вызывает исчезновение этого пика. Его проявление точно при температуре сверхпроводящего перехода подтверждено и резистивными измерениями.

В предыдущем разделе мы отмечали, что основной вклад в особенности ВТ в области гелиевых температур вносят дефекты кристаллической решетки и в частности дислокации. Как показано в [1.10], изменения в кристаллической структуре, вносимые путем пла-

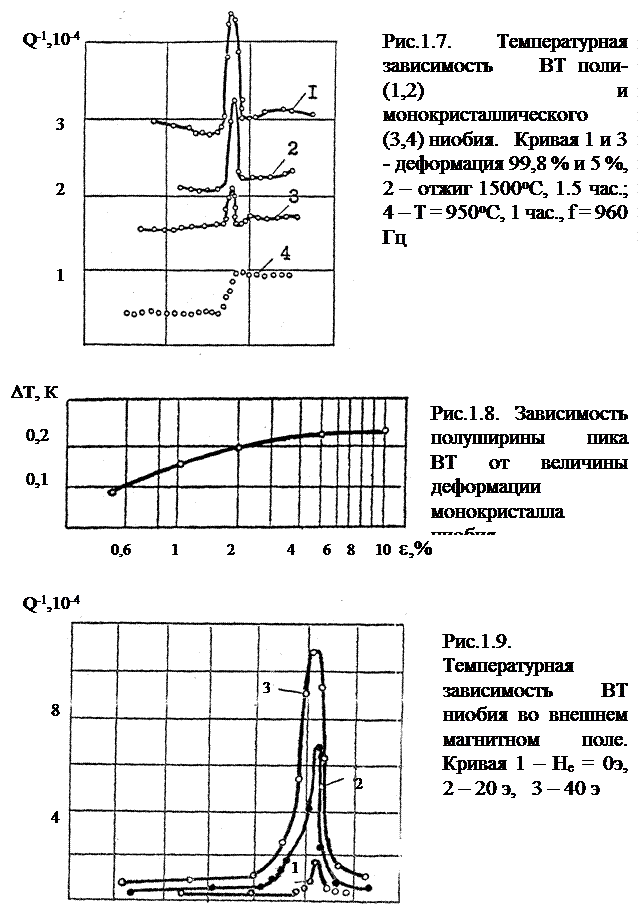
стической деформации, при которой растет плотность дислокаций, вызывают рост фона ВТ и рост пика в области фазового перехода. Конечно при больших пластических деформациях (до 99,8 %), кроме роста плотности дислокаций изменяется величина зерна и концентрация точечных дефектов. Поэтому для чистоты экспериментальных исследований далее были использованы монокристаллы, которые подвергались деформации на различную величину от 0,5 до 10 %. При этом на 3 порядка возрастала плотность дислокаций от 10⁶ до 10⁹ см^-2 и, как следствие, росла полуширина пика ВТ от 0,09 К при деформации на 0, 5% до 0,22 К при увеличении деформации до 10 % (рис. 1.8). Известно, что плотность дислокаций еще можно изменять за счет рекристаллизационного отжига. Так, на рис. 1.7 представлены результаты влияния отжига монокристаллического ниобия предварительно деформированного на 5 %, а также на 99,8 % (кривые 3 и 1). Применялся дополнительный отжиг при 950^оС со временем 1 час и 1500^о С, длительностью 1,5 часа (кривые 4 и 2 соответственно). Видно, что после такого отжига фон ВТ, как и следовало ожидать, снизился (кривые 2 и 4), пики Q^-1 уменьшились или стали экспериментально неразличимы (кривая 4).

Кроме того, проводилось исследование влияния примесей на поглощение низкочастотного звука. Объектом исследований служил монокристаллический ниобий исходной чистоты 99,998 %, который легировался ванадием. Концентрация его (от партии к партии) изменялась в пределах от 0,041 до 1,47 вес %. Оказалось, что в пределах исследуемых концентраций ванадия, при прочих равных условиях, величина пика ВТ не изменялась.

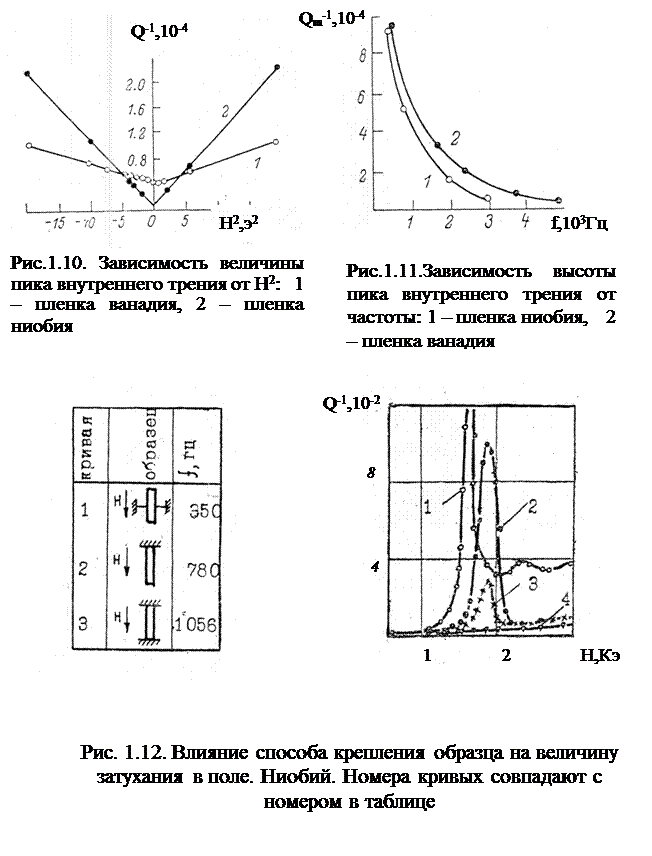
Существенным в вопросе выяснения природы этого пика является влияние частоты собственных колебаний образца. В работе [1.10] показано, что с изменением частоты в пределах 5· 10² – 5 ·10³ Гц положение пика по оси температур остается постоянным, а изменялась его высота (рис. 1.11). И, наконец, последнее – влияние внешнего магнитного поля, т.к. во всех экспериментальных исследованиях, как минимум, присутствовало магнитное поле Земли. В серии экспериментов в одном случае магнитное поле экранировалось, т.е. ослаблялось, в другом – усиливалось с помощью соленоида. Эти исследования методом внутреннего трения показали, как видно из рис. 1.9, что с ростом поля до 60 Э, пики заметно увеличиваются. На рис. 1.10 представлены результаты исследования пленок ниобия и для сравнения пленок ванадия. Зависимость величины пика ВТ прямо пропорциональна квадрату напряженности магнитного поля. Это свидетельствует о том, что за появление дополнительного затухания ответственны джоулевы потери. Однако само появление пика ВТ не связано с наличием магнитного поля: зависимости Q^-1(Н²) выходят не из нуля, т.е. и в отсутствии поля пик существует.

Оценки величин различных вкладов в затухание низкочастотного звука, которые приведены выше (по формулам 1.8 и 1.9) показывают, что при гелиевых температурах фононный и электронный вклады малы и заметно меньше экспериментально наблюдаемых величин.

Согласно [1.7] основной вклад в низкочастотное поглощение звука вносит термоактивируемое движение дислокаций. Однако в области сверхпроводящего перехода электронный вклад может аномально увеличиваться из-за флуктуаций параметра порядка, интенсивность которых возрастает вблизи Т_к [1.12]. В [1.13,1.10] было рассмотрено флуктуационное поглощение звука как ниже, так и выше критической температуры. Результаты, полученные в этих работах можно представить для величины внутреннего трения вблизи фазового N – S перехода в следующем виде:

а) Т ≤ Т_к

Q_(-)^-1 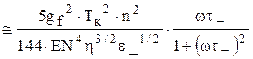, (1.15)

б) Т ≥ T_к

Q₍₊₎^-1 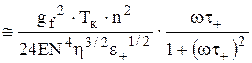, (1.16)

где τ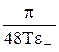_(-) = ; τ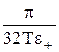₍₊₎ = ; ε_- = ; ^,

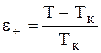g_f² = 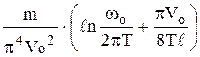; n = ;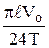

V_о – скорость Ферми; ℓ - длина свободного пробега электронов; m – масса электрона; N – плотность состояний на поверхности Ферми; Е – модуль Юнга; Т_к – температура, при которой возникает

сверхпроводимость. Из анализа выражений (1.15) и (1.16) следует, что при Т = Т_к1 (I + ωτ_о) существует пик внутреннего трения.

max Q^-1 _{f_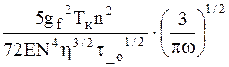}= , (1.17)

где τ_-о = 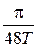и при Т = Т_к (I + ωτ_+о) существует второй пик внутреннего трения.

max Q^-1_f+ = , (1.18)

где τ_+о = .

При экспериментальных исследованиях внутреннего трения любых сверхпроводников в соответствии с рассмотренной моделью должен наблюдаться узкий пик ВТ при критической температуре, но из-за ограниченности разрешающей способности установки по стабилизации температуры эти пики сливаются в один, который и наблюдается. В рамках данной флуктуационной модели связывалось увеличение поглощения энергии звуковых колебаний с их частотой и плотностью дислокаций: пик пропорционален 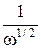, что видно из рис. 1.11, а также прямопропорционален плотности дислокаций (см., например, рис. 1.2, 1.8, 1.7). Здесь необходимо учитывать, что между шириной и высотой пика есть корреляция.

Оценки для сверхпроводника со следующими параметрами: Т_к ~ 10 К, V_o= 10⁵см · с^-1 , ℓ ~ 10^-9см, Е = 10¹²дин·см^-2, ω = 2π ·10³ рад с^-1, ρ = 10 г см ^-3 дают величину флуктуационных поправок из выражений (1.17) и (1.18) для пика Q^-1_f как выше, так и ниже Т_к. Полученные значения по порядку величины хорошо совпадает с экспериментальными данными (для ниобия max Q^-1_f = 3 ·10^-4). Кроме того, величина максимума по ту и другую сторону от Т_к, , как видно из (1.17) и (1.18), пропорциональна ω^-1/2, что по характеру, как мы отмечали, согласуется с результатами эксперимента.

1.4. Магнитоупругие и магнитомеханические эффекты в сверхпроводниках

Ранее мы отмечали, что сверхпроводник характеризуется внутренним параметром порядка. Внешнее магнитное поле вызывает пространственную неоднородность этого параметра порядка, которая приводит к появлению ряда специфических механизмов поглощения звука как в области ультразвука, так и низкочастотного звука и инфразвука. Выше отмечали, что в данной работе в целом и в главе в частности будем рассматривать область низкочастотного звука (или звука). Область ультразвука освещена в ряде работ (см., например, [1.14]), как и область инфразвука [1.15, 1.16]. В области звуковых частот, исследования проводятся на образцах в виде пластин, которые совершают упругие колебания [1.17] или укреплены на струне, и тогда деформацию воспринимает подвеска из парамагнитного металлического материала [1.18]. Эффекты, которые обнаружены в колеблющемся со звуковой частотой сверхпроводнике, в первом случае называются магнитоупругими и теоретически на основе магнито-гидродинамических представлений подробно рассмотрены в работе [1.19], а во втором – магнитомеханическими эффектами, которые изучены в [1.18] на основе представлений магнитной поляризуемости. Было показано [1.11] (см. рис. 1.12), что вне зависимости от способа крепления сверхпроводящей пластинки, при одинаковых прочих внешних условиях, в затухании колебаний (см. кривые 1,2,3) происходят сходные физические процессы: в области смешанного состояния наблюдается максимум потерь.

1.4.1. Магнитоупругие эффекты в звуковом диапазоне частот

В 70 – 80^х годах исследования сверхпроводников в магнитном поле выявили довольно непростой характер затухания их колебаний (см., например, [1.14, 1.17, 1.20]). В области смешанного состояния наблюдалось аномальное по характеру поглощение энергии колебаний образца (см. обзор [1.14]). Сами образцы в виде пластины, закрепленной консольно (четверть волновой вибратор) [1.14,1.20] или с обоих концов (полуволновой вибратор) [1.17], помещались в продольное постоянное магнитное поле, где наблюдалось наибольшее затухание и изменение модуля Юнга (можно квадрата частоты) по сравнению со случаем поля, перпендикулярного плоскости пластины, где эти величины намного меньше. В работе [1.20] высказывалась идея о вкладе в модуль упругости решетки вихрей, который, в свою очередь, определяется квазиупругим взаимодействием магнитного момента колеблющегося образца с магнитным полем. Подобные результаты получены в [1.21, 1.22], где проводились исследования частоты колебаний сверхпроводящих пластин ниобия [1.21] и проволочек [1.22] Nb – Ti в продольном магнитном поле и в поле транспортного тока. Показано, что частота также возрастает при росте поля, но уменьшается с увеличением тока. Таким образом, в некоторых работах, например [1.20], связываются наблюдаемые эффекты аномального поглощения энергии в смешанном состоянии с увлечением кристаллической решеткой закрепленных вихрей, которые создают возвращающую силу, и тем самым появляется дополнительная жесткость.

Известна единственная попытка объяснения результатов работ [1.15 и др.]. Автор [1.23]рассмотрел в поперечном магнитном поле Н_е сверхпроводящий цилиндр со свободными и закрепленными вихрями, плотности которых равны (П_св и П_зак). Предполагается, что амплитуда колебаний цилиндра мала, угол поворота закрепленных вихрей совпадает с углом поворота цилиндра, а диссипация энергии вызвана вязким движением свободных вихрей. Если в процессе колебаний цилиндра дополнительные вихри не успевают проникать в образец из-за поверхностного барьера, то П_св –const. Тогда коэффициент затухания и частота колебаний имеют вид:

Г = Г_о + , (1.19)

, (1.20)

где V и R – объем и радиус цилиндра, I – момент инерции колебательной системы, η = 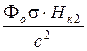- коэффициент вязкости вихрей, Г_о – затухание, обусловленное другими механизмами, ω_о – нулевая частота колебаний, связанная с упругими свойствами колебательной системы. В случае быстрой релаксации вихрей в больших полях (Н_е >>Н_к1) вычисления дают:

Г = Г_о + , (1.21)

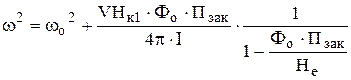. (1.22)

В выражениях (1.19) и (1.21) при Н_е → Н_к2 затухание, связанное с вихрями, переходит в затухание на токах Фуко Г_ф = 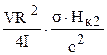. Из этих выражений видно, что в общем случае на монотонный рост Г ~ Н_е накладывается пик, обусловленный знаменателем , т.е. 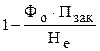. С физической точки зрения это дополнительное поглощение возникает в следствии отталкивания свободных вихрей от закрепленных, которое приводит к возрастанию амплитуды колебаний свободных вихрей относительно сверхпроводника и, следовательно, к возрастанию потерь, связанных с вязким движением вихрей.

Однако существует и другая модель, в рамках которой нашли объяснение все наблюдаемые особенности в изменении параметров колеблющейся пластины сверхпроводника [1.17].

В этой работе исследовалось затухание колебаний и изменение их частоты в зависимости от магнитного поля при постоянной температуре также на пластинках, колеблющихся с частотой 1 ÷ 6 кГц. В качестве образцов исследовались поли- и монокристаллический алюминий (чистоты 99,951 %), свинец (99,9996 %), ванадий и ниобий. Отметим, что характерным для всех исследованных металлов является квадратичная по магнитному полю зависимость фона Q^-1(Н_е) и Δf/f_н = 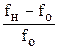, если они находятся в нормальном состоянии (Аℓ при Т > Т_к) (Рb при Н_е > Н_к), как показано на рис. 1.13 и 1.14. Крутизна этих кривых Q^-1(Н_е) = Н_е (рис. 1.13) определяется проводимостью металла в нормальном состоянии: чем она меньше, тем слабее влияние магнитного поля. В сверхпроводящем состоянии характер кривых Q^-1(Н) зависит от рода сверхпроводника и частоты колебаний. У сверхпроводника 1 рода (свинец с Т_к = 7,2 К, а рабочая температура 4,2 К) в области N- S перехода наблюдается резкий скачек (рис.1.14). Сверхпроводник 2 рода (ванадий) ведет себя иначе: в смешанном состоянии имеется пик Q^-1 (рис. 1.15), величина которого зависит от частоты, и модуль в этой же области магнитных полей также проходит через максимум, хотя и смещается в сторону меньших значений. Из экспериментальных данных следует, что с ростом частоты высота пиков обратно пропорциональна квадрату частоты (рис. 1.11).

Обсуждение проводится в рамках теории магнитоупругого взаимодействия через комплексную проводимость σ и магнитную проницаемость μ и представлениях общей теорией магнитоупругости тонких оболочек и пластин [1.19]. При этом учитывается комплексный характер проводимости и ее зависимость от частоты. Решение проводится для пластин с бесконечными размерами (рис. 1.16) в параллельном оси Х магнитном поле с учетом того, что формой колебаний является цилиндрическая поверхность с образующей параллельной оси у. Решением являются плоские волны, распространяющиеся вдоль оси Х [1.17].

h_Z = h_o· exp i (ωt - kX);

e_y = e_o · exp i (ωt - kX); (1.23)

δ = δ_o · exp i (ωt - kX),

где h_Z, e_y – компоненты индуцируемых движением пластины переменных магнитных и электрических полей, δ – смещение пластины.

Далее характеристическое уравнение для определения частоты колебаний записывается в виде

, (1.24)

где 2d – толщина пластины, ρ – плотность материала, k = 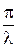, λ – длина полуволны, ω – циклическая частота колебаний, ω_о- частота собствен-

ных колебаний пластины в отсутствии магнитного поля. В уравнении (1.24) введены обозначения

;

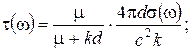
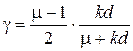ω_о² = (D/2ρd) k⁴, D = 2d³E/3 (1-v²) - цилиндрическая жесткость, Е – модуль Юнга, v – коэффициент Пуассона, с – скорость света.

Для того чтобы проанализировать выражение (1.24), необходимо знать величину комплексной проводимости сверхпроводника в смешанном состоянии, что сложно, поэтому рассмотрим область полей, близких к Н_к2 (или Н_к), где выполняются условия

μ ≤ 1 ; σ ~ σ_n f (Н), (1.25)

здесь σ_n – проводимость сверхпроводника в нормальном сост