Исследование неразветвленной цепи переменного тока
Приступая к работе, обратить внимание на соотношения между напряжением сети и напряжениями на отдельных участках цепи в режиме резонанса, на конструкцию индуктивности и емкости и
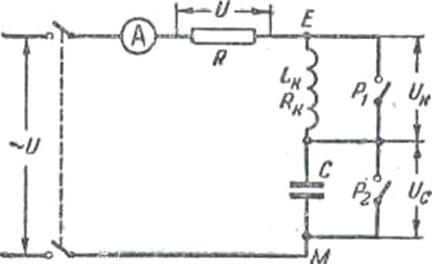
Рис. 9. к практической работе 6.
выяснить, каким путем можно изменять их величину. Так как в режиме резонанса напряжений ток достигает наибольшей величины, то амперметр нужно выбирать исходя из этого режима; Оценив величину активного сопротивления, подсчитать приближенно значение тока в режиме резонанса напряжений.
При выполнении работы провести три цикла измерений:
1) цепь содержит одно активное сопротивление;
2) цепь содержит активное сопротивление и индуктивность;
3) в цепь включены все три сопротивления.
С помощью моста для измерения сопротивлений или иным способом определить активное сопротивление RK индуктивности. Замкнув рубильники Р1 и Р2 получить цепь с активным сопротивлением. Измерив ток и напряжение, вычислить величину этого сопротивления .
Разомкнув рубильник Р1, получить цепь с активным сопротивлением и индуктивностью. Измерив, ток и напряжение всей цепи, подсчитать полное сопротивление катушки, причем под активным сопротивлением цепи следует подразумевать сумму активного сопротивления R и активного сопротивления катушки RK. Кроме того, вычислить активную мощность Р2 и коэффициент мощности cos φ2. Результаты измерений и вычислений записать в таблицу .
| № измерения | Измеряются | Вычисляются | ||||
| I2 | U2 | z2 | ХL | соs φ2 | Р2 | |
| а | в | ом | ом | - | вт | |
Разомкнув и второй рубильник, получить последовательную цепь с активным сопротивлением, индуктивностью и емкостью.
Обратить внимание на ток в цепи. Как он изменился после введения в цепь еще одного сопротивления? Записав новые значения тока и напряжения, определить полное сопротивление цепи в этом случае z3, результирующее реактивное сопротивление, величину емкостного сопротивления, cos φз и величину активной мощности Р3. Результаты измерений и вычислений записать в таблицу .
| № измерения | Измеряются | Вычисляются | ||||||||||
| Iрез | I3 | U3 | Uк | UС | UЕМ | z3 | Х | ХС | соsφ3 | Р3 | ХL | |
| а | а | в | в | в | в | ом | ом | ом | - | вт | ом | |
Подсчитанное значение Хс окажется либо больше, либо меньше XL. В зависимости от этого решить вопрос, что нужно сделать для получения в цепи режима резонанса напряжений? Добиться его.
Записать значение тока цепи в этом случае, напряжение UEM, напряжения на индуктивном и емкостном сопротивлениях. Вычислить величины, указанные в таблице 11, и занести их туда. Сравнить ток I2 с током I3. Почему I2<I3, хотя в последнем случае в цепь добавлено еще одно сопротивление? Чем объяснить, что cos φ3 >cos φ2? Почему Р3>Р2. Почему в режиме резонанса напряжение UEM≈0, a XL≈XC?
Чем объяснить, что в режиме резонанса напряжений ток Iрез больше токов в иных режимах, a cos φрез≈1?
Можно ли компенсировать сдвиг фаз, созданный индуктивной нагрузкой, включением последовательно с ней емкости соответствующей величины?
Последовательная цепь с активным, индуктивным и емкостным сопротивлениями. Векторная диаграмма и сдвиг фаз. Для того чтобы выяснить явления, происходящие в такой цепи (рис, 10,а), необходимо построить ее векторную диаграмму.
Допустим, что XL>XC. Задавшись масштабом тока и отложив вектор последнего, построим вектор общего напряжения U путем геометрического сложения напряжений на отдельных участках цепи (рис. 10,6). Напряжение на активном сопротивлении всегда совпадает по фазе с током, текущим через него, поэтому, задавшись масштабом напряжений, откладываем вектор Ua в направлении вектора тока. Напряжение на индуктивном сопротивлении опережает ток в нем па 90°, поэтому вектор UL пристраиваем к концу вектора активного напряжения, направив его вверх перпендикулярно вектору тока. Вектор напряжения Uc пристраиваем к концу вектора UL, направив его вниз перпендикулярно вектору тока, так как напряжение на зажимах емкости отстает от тока в ней на 90°. Замыкающая, проведенная из начала первого вектора до конца последнего (ОВ), представляет собой сумму этих трех векторов, то есть напряжение на зажимах цепи.
Из векторной диаграммы видно, что напряжение опережает ток на угол φ, причем угол φ получился меньше того, который был бы в цепи при отсутствии в ней емкости (пунктир ОА).
Треугольник ОВС - является треугольником напряжений этой цепи. При рассмотрении его видно, что напряжения находятся в таких же соотношениях, как и в предыдущих случаях, но реактивная составляющая Uр, в свою очередь, состоит из двух составляющих UL и UС.
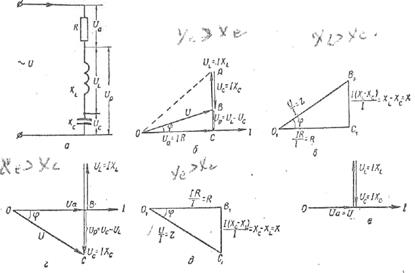
Рис. 10. Общий случай последовательной цепи:
а — схема цепи: б, г и е — векторные диаграммы; в и д—треугольники сопротивлений.
Из векторной диаграммы UP=UL- UC = IXL—IXС = I(XL—ХС).
Разделив все стороны треугольника напряжений на величину силы тока, получим треугольник сопротивлений О1 В1 С1 (рис. 10, в).
Из треугольника сопротивлений следует, что результирующее реактивное сопротивление цепи X равно разности индуктивного и емкостного сопротивлений. Емкостное сопротивление как бы частично уничтожает индуктивное, а полное сопротивление цепи
z = 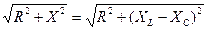
Математическое выражение закона Ома для этого случая остается таким же, как и для предыдущего случая,
I = 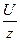
Таким образом, анализируя векторную диаграмму и отдельно треугольники напряжений и сопротивлений, мы можем заключить, что когда в последовательной цепи преобладает индуктивное сопротивление, то есть XL>XC, то она ведет себя в целом, как цепь индуктивная. Например, если активное сопротивление цепи 20 ом, индуктивное 80 ом и емкостное 30 ом, то цепь можно считать состоящей из активного сопротивления 20 ом и индуктивного 50 ом.
Вычисления активной, реактивной и полной мощностей, активного и реактивного токов, активной и реактивной проводимостей можно проводить так же, как для любой индуктивной цепи,
Если в цепи преобладает емкостное сопротивление (XC>XL_), то на векторной диаграмме вектор UC больше вектора UL; а результирующее реактивное напряжение Up равно разности емкостного и индуктивного напряжений (рис.10,г). В этом случае ток опережает напряжение на некоторый угол φ, и цепь ведет себя как цепь емкостная.
Треугольник сопротивлений можно получить как обычно, разделив все стороны треугольника напряжений на величину силы тока I (рис. 10. д).
Пример. Последовательно с катушкой, обладающей активным сопротивлением 24 ом и индуктивностью 0,07 гн, включен конденсатор емкостью 79,6 мкф. Определить характер нагрузки, напряжение на ее зажимах, активную мощность и сдвиг фаз, создаваемый этой нагрузкой, если сила тока в катушке 7 а.
Решение. XL=2πfL=2 · 3,14 · 50,0 · 0,07=22 ом;
Хс= 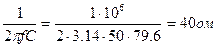
Так как XC>XL, то нагрузка имеет емкостный характер и ток в ней опережает напряжение на некоторый угол φ.
z = 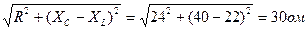
Напряжение на зажимах цепи U =Iz= 7 · 30 =210в
Коэффициент мощности
cos φ = 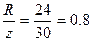 ; <φ = 36045
; <φ = 36045
Активная мощность цепи
Р = UI cos φ = 210·7·0,8= 1176 вт.
Резонанс напряжений. Особый интерес представляют явления, которые наблюдаются в последовательной цепи при равенстве индуктивного и емкостного сопротивлений (рис.10,е). Из векторной диаграммы видно, что при равенстве индуктивного сопротивлений напряжение на зажимах всей цепи (U) равно напряжению на ее активном сопротивлении (Uа) и цепь ведет себя как чисто активная. Это объясняется тем, что при ХL = ХС влияние на цепь индуктивного сопротивления скомпенсировано влиянием емкостного, то есть они как бы полностью взаимно уничтожают друг друга. В результате этого ток в цепи становится максимальным, но так как отсутствует лишь влияние индуктивного и емкостного сопротивлений, а сами они в цепи имеются, то этот максимальный ток проходит и через них, вызывая как в одном, так и в другом падение напряжения (UL и UС).
Явление совпадения по величине падения напряжений на индуктивном и емкостном сопротивлениях в последовательной цепи переменного тока называется резонансом напряжений. В режиме резонанса напряжений
z = 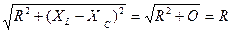
Ток в цепи 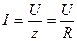 максимален, так как знаменатель в этом случае минимален. При этом < φ = 0, а соs φ=1.
максимален, так как знаменатель в этом случае минимален. При этом < φ = 0, а соs φ=1.
Таким образом, в режиме резонанса напряжений явления в цепи протекают так, как будто в ней осталось лишь одно активное сопротивление.
То обстоятельство, что при последовательном подключении емкости угол сдвига фаз, созданный индуктивностью, уменьшается (пунктир ОА на рисунке 10,6),, а при XC = XL становится равным нулю, не удается использовать в потребительских установках для уменьшения сдвига фаз, созданного индуктивными токоприемниками, так как подключение конденсатора последовательно с токоприемником сопровождается увеличением тока. Если считать, что до подключения конденсатора ток был номинальным, то после подключения он станет больше номинального, что для токоприемника недопустимо, хотя он и будет работать с большим cos φ. Более того, в силовых цепях резонанс напряжений — явление опасное. Так при малом активном сопротивлении цепи ток может достигнуть очень большой величины, на которую установка не рассчитана и кроме того, если индуктивное и емкостное сопротивления велики, этот ток вызовет на их зажимах очень большие напряжения (перенапряжения), в десятки и сотни раз превышающие нормальное рабочее, что может привести к пробою диэлектрика емкости и изоляции индуктивности.
Пример. В цепь последовательно включены катушка с активным сопротивлением 10 ом и индуктивностью 300 мгн и конденсатор емкостью 33,8 мкф. Определить ток в цепи и напряжение на каждом сопротивлении (рис. 10, а). Решение. Индуктивное сопротивление катушки
ХL=2πfL=314·0,3=94,2 ом
Емкостное сопротивление конденсатора
ХС = 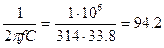 ом
ом
ХL = ХС , следовательно, в цепи имеется резонанс напряжений и
z = 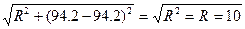 ом
ом
Ток в цепи
I = 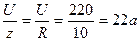
Напряжение на реактивных сопротивлениях
UL =UС= IXL = 22·94,2=2070в; Uа= IR = 22·10=220в
Напряжение на реактивных сопротивлениях больше напряжения сети почти в 10 раз.
Ток до подключения емкости
I= 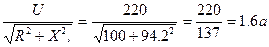
Следовательно, после подключения емкости он возрос почти в 14 раз.
В радиотехнике это явление используется весьма широко, позволяя вследствие образования на зажимах индуктивности и емкости значительных напряжений получить усиление очень слабых радиосигналов.
Для того чтобы специально создать равенство индуктивного и емкостного сопротивлений, необходимо либо ХС подогнать под XL (подобрав конденсатор соответствующей емкости), либо ХL подогнать под ХС (подобрав катушку соответствующей индуктивности).
Так как индуктивное сопротивление катушки и емкостное сопротивление конденсатора зависят от частоты, причем при изменении последней они изменяются взаимообратно (если с увеличением частоты ХL увеличивается, то ХС — уменьшается, и наоборот), то даже при любой катушке и любом конденсаторе в цепи можно добиться резонанса напряжений, подобрав частоту, при которой XL этой катушки окажется равным ХС конденсатора.
Эту частоту обычно называют резонансной и обозначают fрез. Ее можно определить, имея в виду, что при этой частоте XL = XC или 2πfpeзL = 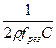 , откуда 4π2f2резLС=1, или f2рез =
, откуда 4π2f2резLС=1, или f2рез = 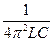
Окончательно
fрез = 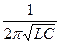
В этой формуле L измеряется в генри, С – в фарадах, fрез – в герцах.
Пример Определить резонансную частоту для цепи, изображенной на рисунке 10а, если индуктивность катушки 4 гн, а емкость конденсатора 1 мкф. Решение.
fрез = 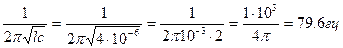
Это значит, что, если к цепи подвести переменное напряжение с частотой 79,6 гц, емкостное сопротивление конденсатора окажется равным индуктивному сопротивлению катушки.
Дата добавления: 2020-03-17; просмотров: 1507;











