Какое напряжение U надо приложить к горизонтально расположенным пластинам, чтобы электрон не смог вылететь за их пределы?

Решение:

Прежде чем начать решать задачу, несколько уточним ее условие. Если бы не было напряжения между горизонтальными пластинами, то электрон, продолжал бы двигаться прямолинейно и беспрепятственно покинул их пределы.

Но если на пластины подается какое-то напряжение, траектория движения электрона искривляется.

Пусть нижняя пластина заряжена положительно, а верхняя отрицательно. Создается электрическое поле, вектор напряженности которого направлен снизу вверх. Электрон начинает приближаться к нижней пластине. Чем больше напряжение между пластинами, тем сильнее искривляется траектория электрона. При каком-то напряжении электрон попадет на край нижней пластины. Ясно, что при большем напряжении электрон будет попадать на саму пластину.

Если найти напряжение, при котором электрон ударяется о край пластины, то при любом напряжении, большем найденного, электрон не покинет их пределы.

Данную задачу можно разбить на две, относительно независимые задачи: о движение электрона в поле вертикально расположенного конденсатора и на движение в поле горизонтально расположенного конденсатора.

Подзадача 1

Поле вертикально расположенных пластин.

Применим к описанию движения электрона энергетический подход.

e v v0 = 0     - + U0

В электрическом поле электрон разгоняется и к моменту вылета из отверстия в пластине приобретает некоторую скорость и кинетическую энергию Ек. Эта энергия приобретается за счет совершения работы электрическим полем. Работа равна изменению кинетической энергии электрона. Начальная кинетическая энергия электрона равна нулю, значит работа равна кинетической энергии, которую электрон приобрел к моменту вылета из конденсатора: А = Ек.

Работа поля по перемещению заряженной частицы из одной точки в другую равна произведению заряда электрона на напряжение:

А= ;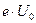

Приравняем правые части уравнений: .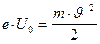

Полученное равенство позволяет найти скорость электрона к моменту его вылета за пределы вертикально расположенных пластин:

.

Подзадача 2

Электрон, летящий горизонтально со скоростью 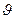, влетает в электрическое поле, вектор напряженности которого направлен вертикально.

Двигаясь в этом поле, электрон проходит путь L и попадет в край пластины. При этом он снижается на расстояние x/2.

Движение электрона в электрическом поле конденсатора аналогично движению тела в поле тяжести, если тело брошено горизонтально.

Тело, брошенное горизонтально, в поле тяжести движется по ветке параболы. Вероятно, электрон тоже движется по ветке параболы.

X x/2 - U + F a

Если на тело действует сила, то она сообщает телу ускорение. В данном случае – это какое-то ускорение.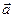

Сложное движение по параболе можно рассматривать как сумму двух независимых движений по горизонтали и по вертикали.

По горизонтали тело движется с постоянной, а по вертикали с переменной по величине скоростью.

Выбираем инерциальную систему отсчета. Точку отсчета совмещаем с положением электрона, когда он попадает в электрическое поле. В этот же момент начинаем отсчитывать время. Совмещаем с данной точкой систему координат. Одну ось направляем горизонтально, другую вертикально.

Учитывая, что время движения электрона по горизонтали равно времени падения его на нижнюю пластину, записываем: .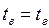

Время движения по вертикали может быть найдено из кинематического уравнения, связывающего ускорение и перемещение электрона в вертикальном направлении: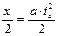

Время движения по горизонтали: 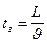, где L – пройденный путь, 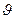– скорость электрона (она найдена в первой подзадаче).

Ускорение сообщается силой: .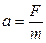

Сила выражается через заряд электрона и напряженность электрического поля: .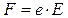

Напряженность электрического поля между пластинами связано с напряжением, приложенным к ним: 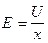, где x – расстояние между пластинами.

Производя последовательные подстановки, найдем неизвестное напряжение U: ;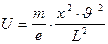

Задача № 3