Некоторые методы построения блочных корректирующих кодов
1. Коды, построенные на основе увеличения кодового расстояния
Идея обнаружения и исправления ошибок в таких кодах заключается в следующем. Для передачи символов сообщения используют не все N возможных комбинаций элементов символов кода длиной n, а только часть из них N0, которые называются разрешенными символами кода. Оставшиеся ΔN комбинаций (ΔN = N – N0)называют запрещенными. Ошибка обнаруживается тогда, когда приемник получает запрещенную комбинацию элементов символов кода. Всякий код, у которого ΔN > 0, способен обнаруживать ошибки в ΔN случаях из N. Доля обнаруживаемых ошибок (s) определяется выражением:
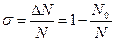 .
.
По формуле (2.9) легко определить избыточность такого корректирующего кода (Rk ):
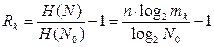 ,
,
где H(N0 )—энтропия кода с объемом алфавита N0 ;
H(N)—энтропия кода с объемом алфавита N;
n— число элементов в кодовом символе;
mk— основание кода.
Исправление ошибок в корректирующих кодах заключается в том, что, обнаружив ошибку, определяют кодовое состояние от полученной запрещенной комбинации ki до всех разрешенных символов кода kj (j=1, 2, ..., N0) и в качестве переданного символа кода считается тот из разрешенных символов кода, до которого расстояние минимально. Таким образом, исправление ошибок корректирующими кодами производится с помощью трех последовательных операций:
- определения кодового расстояния между принятой кодовой комбинацией и разрешенными кодовыми символами;
- отыскания минимального кодового расстояния;
- присвоение принятой кодовой комбинации значения ближайшего к ней (по кодовому расстоянию) разрешенного кодового символа.
Например, в трехзначном равномерном двоичном коде число возможных кодовых комбинаций 8:
000, 001, 010, 011, 100, 101, 010, 111,
кодовое расстояние между которыми (dij) равно 1. Ошибка в любом одном элементе символа кода превращает передаваемый разрешенный кодовый символ в другой, но так же разрешенный.
Если увеличить кодовое расстояние (dij=2), т.е. сделать разрешенными кодовые символы отличающимися в двух элементах (001, 111, 010, 100), то помехозащищенность кода увеличивается. Действительно, если в процессе передачи возникает ошибка только в одном элементе любого разрешенного символа, то эта комбинация превращается в запрещенную, что свидетельствует о появлении одиночной ошибки в символе кода, хотя и неизвестно какой именно. Такой код не позволяет выяснить какой конкретно из передаваемых элементов искажен, а значит и не позволяет исправить ошибку.
Если еще больше увеличить кодовое расстояние (dij=3), т. е. сделать разрешенными кодовые символы отличными друг от друга в трех элементах (например, 111, 000), то помехозащищенность кода еще более возрастает.
Действительно, если в процессе передачи произойдет ошибка в одном или двух элементах любого из двух разрешенных символов кода, то возникнет запрещенная комбинация элементов. Таким образом, применение этого кода дает возможность обнаружить две или, если произойдет только одна ошибка, что более вероятно, то можно восстановить переданный символ кода.
Из приведенного примера видно, что для обнаружения единичной ошибки в символе кода требуется один избыточный элемент в символах кода, чтобы обеспечить минимальное кодовое расстояние (расстояние между разрешенными символами (dij)) равное 2, а для исправления в символах кода одной ошибки необходимо увеличить минимальное кодовое расстояние между символами кода (dij) до 3, т. е. ввести в символы кода два избыточных элемента. В общем случае для избыточных кодов справедливо соотношение:
dij = 1 + p + q ,
где p ≥ q ;
p— количество обнаруживаемых ошибок в символах;
q— количество исправляемых ошибок в символах кода.
Свойства корректирующих кодов по обнаружению и исправлению ошибок, в зависимости от величины минимального кодового расстояния между разрешенными символами, приведены в таблице 2.7.
Таблица 2.7
| Характеристика кодов. | Свойства кодов. | ||
| d | p | q | |
| Отличает одну кодовую комбинацию от другой. | |||
| Обнаруживает одну ошибку. | |||
| Обнаруживает и исправляет одну ошибку. | |||
| Обнаруживает две ошибки. | |||
| Обнаруживает две ошибки и исправляет одну. | |||
| Обнаруживает три ошибки. | |||
| Обнаруживает и исправляет две ошибки. | |||
| Обнаруживает три ошибки и исправляет одну. | |||
| Обнаруживает четыре ошибки. | |||
| и т. д. |
2. Коды, построенные на основе проверки на четность.
Этот метод построения помехозащищенных кодов заключается в том, что в каждый кодовый символ двоичного кода добавляется для проверки один избыточный элемент (0 или 1) так, чтобы общее количество единиц в каждом символе кода было четным. Построение такого кода на примере двухэлементного двоичного кода представлено в Таблице 2.8.
Таблица 2.8.
| Неизбьггочные кодовые символы. | Kонтрольный избыточный элемент. | Полные кодовые символы, обнаруживающие единочную ошибку. |
При получении символов, таким образом построенных избыточных кодов, перед их раскодированием производится проверка их на четность. При одиночной ошибке количество единичных элементов в кодовом символе станет нечетным, что дает возможность обнаружить ошибку и осуществить повторную передачу.
Близким к рассмотренному способу построения корректирующих кодов является способ добавления контрольных избыточных элементов, на основе суммирования по основанию «2» элементов символов двоичного кода и на основе простейших логических операций над элементами символов кода.
3. На основе защиты сдвоенными элементами.
В этом коде количество элементов в символах двоичного кода удваивается, причем к каждому элементу «0» приписывается «1», а к каждому элементу «1» приписывается элемент «0». Например, исходный кодовый символ 11010 по этому методу кодируется следующим образом:

Рис. 2.7. Метод построения корректирующего кода на основе защиты сдвоенными элементами.
Полученный корректирующий код позволяет обнаружить одиночную ошибку в каждом разряде путем сложения по модулю 2 каждой пары элементов символа корректирующего кода. Если вследствие единичного сбоя в какой-либо паре сумма будет равна 0, то это является сигналом ошибки в данном разряде.
Дата добавления: 2018-11-26; просмотров: 1030;











