Теоретические основы помехоустойчивого кодирования

Теоретические основы помехозащищенного кодирования сообщений базируются на основной теореме Шеннона о кодировании для канала с помехами. Эта теорема гласит:

1. При любой производительности источника сообщений, меньшей чем пропускная, способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки.

2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.

Анализируя теорему, важно отметить, что она устанавливает теоретический предел процесса передачи информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки и показывает, что помехи в канале не накладывают ограничений на точность и достоверность передачи сообщений, а ограничения накладываются лишь на скорость передачи, при которой может быть достигнута сколь угодно высокая достоверность передачи.

Теорема, к сожалению, не указывает конкретных путей построения кодов, обеспечивающих надежность передачи, однако она доказывает, что такие пути существуют.

Для определения конкретных направлений, обеспечивающих повышение надёжности и достоверности передачи сообщений, обратимся к общей информационной модели системы передачи сообщений, представленной на рис. 2.4.

Рис. 2.4. Общая информационная модель системы передачи сообщений.

Пусть 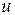– исходное сообщение, генерируемое источником сообщения, датчик сообщения преобразует его в сигнал, 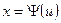затем этот сигнал проходит по каналу и поступает на приёмник, в котором преобразовывается в сообщение : .

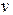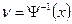Таким образом, процесс передачи сообщений описывается в следующем образом (Рис.2.5.):

— на передающем конце канала пространство сообщений 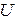преобразуется в пространство сигналов ;

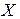— на приёмном конце канала из пространства сигналов 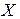восстанавливается пространство сообщений .

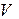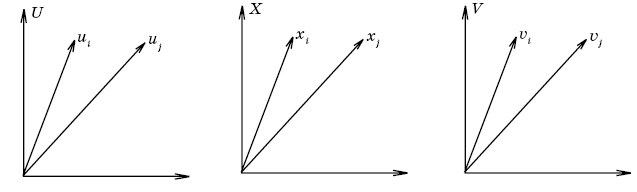
Рис. 2.5. Иллюстрация процесса передачи сообщений по каналу.

При отсутствии помех выполняется однозначное соответствие между исходным символом сообщения (u_i) и принятым символом (v_i). Действительно,

,

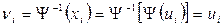При наличии помех сигнал Xпри прохождении через канал будет искажаться и, в общем случае, 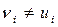, что приводит к искажению исходного сообщения и вызывает трудности в разделении и опознании исходных символов сообщений. Для безошибочного приёма необходимо идентифицировать принятое сообщение v, то есть определить, какому исходному сообще­нию оно соответствует.

Выполнить эту идентификацию можно следующим образом. Если собственные шумы в приёмнике отсутствуют, то можно однозначно определить принятый сигнал x, соответствующий полученному сообщению v:

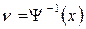
и определить положение сигнала xв пространстве сигналов X(Рис. 2.6.).

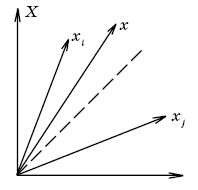
Рис. 2.6. Положение сигнала xв пространстве сигналов X.

Вектору xможно присвоить значение ближайшего к нему известного вектора из пространства сигналов X, то есть 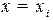, если

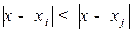
для любого .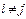

Приемник, работающий по выше рассмотренному принципу идентификации, называют идеальным приемником.

Ошибка приема идеального приемника (прием сообщения 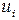вместо переданного 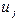) происходит лишь тогда, когда сигнал xпод действием помех переходит границу раздела областей этих сообщений, то есть тогда, когда

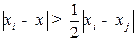
Вероятность появления такой ошибки может служить мерой помехоустойчивости или надежности системы связи (П):

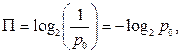
(2.9.)

где 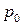– вероятность появления ошибки на выходе приемника.

Очевидно, что с увеличением расстояния между векторами x_i и x_j помехоустойчивость повышается.

Если величина помехи ξ определяется как ξ = x_i - x, то для безошибочного приема сообщения x необходимо выполнение условия:

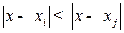
или

,

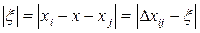где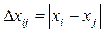

И тогда условие безошибочного приема запишется в виде:

.

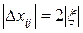В случае, если помеха (ξ) имеет плотность распределения вероятностей f(ξ), то вероятность появления ошибки 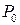можно определить из выражения:

В общем случае пространство сообщений Uимеет размерность n (например, каждый символ этого сообщения состоит из n элементов). Тогда условие безошибочного приема получим из следующих соображений.

Так как

,

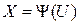то

,

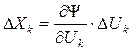а

,

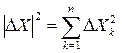где 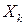– k-я координата пространства X.

Следовательно,

.

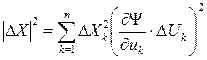Есл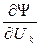и и 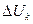– независимы, то минимальное расстояние между сигналами 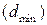должно удовлетворять условию:

,

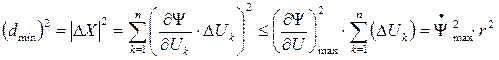где ;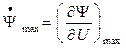

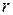– расстояние между двумя ближайшими сообщениями.

Корректирующее кодирование применяют в тех случаях, когда возможности других более простых способов повышения помехозащищенности (таких как многократное повторение или фильтрация) исчерпаны. Это обус­ловлено усложнением систем передачи информации при введении кодирующих устройств.

Как следует из выше приведённых выводов теории помехоустойчивости, основной практический принцип построения корректирующих (помехозащищенных) кодов основывается на допущении, что принятый кодовый символ после воздействия на него помехи всегда остается в некоторой близости от кодового символа, однозначно соответствующего передаваемому символу исходного сообщения. Это позволяет в дальнейшем отождествить принятый символ с ближайшим к нему символом кодового алфавита путём нахождения минимального расстояния из всех расстояний между принятым символом и всеми символами кодового алфавита.

Создание специальных помехоустойчивых цифровых кодов, позволяющих не только обнаружить, но и при определенных условиях исправить возникающие ошибки, основано на увеличении минимального расстояния между символами кодового алфавита (d_min) путём. увеличения избыточности кодов.

Это достигается введением при кодировании дополнительных (избыточных) элементов символов кода, которые удовлетворяют некоторым дополнительным условиям и проверка которых дает возможность обнаружить и исправить ошибки.

Принципы практического построения корректирующих кодов удобно продемонстрировать на примере блочных систематических кодов (в частности алгебраических кодов), как наиболее наглядных и широко применяемых.

Для алгебраических (n, k) корректирующих кодов избыточность кода (R_n, R_k) определяется выражениями:

, ;

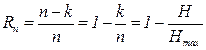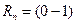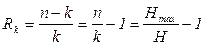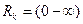, , (2.9)

где n — число элементов в кодовом символе;

k — число информационных элементов в кодовом символе (или минимально возможное число элементов в кодовом символе.

Величина R_k, с областью изменения от 0 до ∞ предпочтительнее, так как лучше отвечает смыслу понятия избыточности.

Коды, обеспечивающие заданную помехоустойчивость при минимально возможной избыточности, называют оптимальными.

Очевидно, что при оптимальном кодировании, когда лишние элементы в кодах отсутствуют, т.е. когда n = k, избыточность равна 0.

Для оценки кодов с точки зрения возможности обнаружения и исправле­ния ошибок используют понятие кодового расстояния (число кодовых переходов для двоичных кодов) d_ij.

Кодовым расстоянием (d_ij) между кодовыми символами k_i и k_j называют суммарный результат сложения по модулю m_k одноименных разрядов кодовых символов k_i и k_j:

,

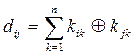где ;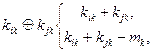

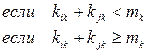k_ik и k_jk — k разряд кодовых символов k_i и k_j;

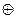— символ сложения по модулю m_k;

m_k — основание кода (основание системы счисления цифрового кода).

Например, если даны символы двоичного числового кода k_i = 10111 и k_j = 01010, то кодовое расстояние между этими символами равно 4 (d_ij= 4).

Кодовое расстояние может быть посчитано и для числовых кодов с иными основаниями, отличными от 2.

Кодовое расстояние иногда называют расстоянием Хемминга.