Информация в непрерывных сообщениях.

Под непрерывным сообщением подразумеваются сообщения, состоящие из символов бесконечного алфавита, т.е. символы такого сообщения представляют собой непрерывное множество из некоторого конечного интервала. Поэтому непрерывное сообщение можно рассматривать как некую непрерывную функцию.

Подходы, приведенные для оценки количества информации, содержащейся в дискретных сообщениях, непосредственно применить к непрерывным сообщениям не удаётся, так как это приводит к результату, противоречащему здравому смыслу.

Действительно, поскольку алфавит источника непрерывных сообщений (L) бесконечен и число символов в сообщении (n) также бесконечно, то и количество информации 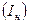, содержащееся в непрерывном сообщении даже конечной длины, равно бесконечности, т.е.

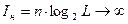
Однако для реальных источников сообщений это противоречие устранимо, т.к. любые реальные источники сообщений обладают следующими особенностями.

Во-первых, реальные источники сообщений обладают инерционностью (т.е. для перехода их из одного состояния в другое требуется конечное время). Это выражается в ограниченности частотного спектра непрерывных сообщений, и, следовательно, к ним применима теорема Котельникова («теорема отсчетов»). Из этой теоремы следует, что любое непрерывное сообщение x(t) длительностью Т иверхнейграничной частотой в спектре 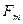может быть представлено последовательностью равноотстоящих мгновенных значений этого сообщения взятых с интервалом Δt = 1/2 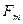.При этом общее число равноотстоящих мгновенных значений не будет превышать значения N:

.

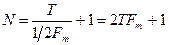Во-вторых, в любых реальных системах всегда присутствуют помехи (шумы), вызванные различными причинами, вплоть до молекулярныи и квантовых. Эти шумы ограничивают число различимых символов сообщения. Действительно, для надежного распознавания соседних символов необходимо, чтобы разность между ними была больше, чем уровень помехи (шума).

При заданной средней мощности помехи (Р_n) и мощности сообщения 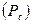число различимых символов (L) непрерывного сообщения x(t) приближенно можно определить из соотношения:

.

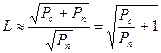Таким образом, любое реальное непрерывное сообщение длительностью Т и с частотным спектром, ограниченным частотой 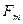, может быть представлено дискретным сообщением из N символов с алфавитом объемом L. В соответствии с формулой определения количества информации по Хартли (1.5), можно получить формулу для оценки максимального количества информации в таком сообщении (I_н):

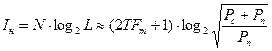(бит) (1.13)

Можно так же подсчитать предельную информационную емкость реального непрерывного сообщения (R):

,

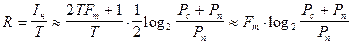при условии, что 2TF_m>>1.

Эта формула устанавливает предельную информационную емкость непрерывного сообщения. Из нее следует, что важнейшими характеристиками любого источника непрерывных сообщений (и канала передачи информации) являются ширина частотного спектра и отношение мощности сообщения (сигнала) к мощности помех.

Следует подчеркнуть, что приведенные выше соотношения справедливы только при условии взаимной независимости и равновероятности появления символов непрерывного сообщения т.к. их вывод основан на использовании формулы Хартли.