Статистическое определение количества информации (по Шеннону).

Этот подход к определению количества информации в сообщениях, учитывающий не равновероятное появление символов сообщения и их статистическую связь, был предложен К.Шенноном в 1946 г.

Рассмотрение этого метода удобно начать с определения количества информации в дискретных сообщениях, символы которых появляются не равновероятно, однако статистическая связь между символами отсутствует.

Пусть, как и ранее, дан источник дискретных сообщений 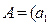, 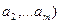с объемом алфавита равным m, который генерирует сообщение, состоящее из n символов. Допустим, что в этом сообщении символ 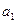встречается раз, символ раз и так далее вплоть до символа 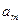, который встречается 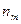раз, причем очевидно, что

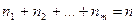
При приеме одного символа 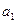, как следует из (1.4), получаем количество информации :

,

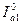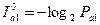где 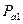- априорная вероятность появления символа .

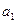А количество информации 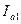, содержащееся в взаимно независимых символах 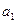, будет равно:

.

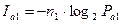Аналогично, в 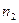символах 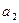содержится количество информации :

,

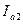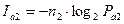и так далее вплоть до

.

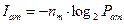Очевидно, что полное количество информации (I_n), содержащееся в сообщении из n символов, равно сумме количеств информации содержащихся во всех m символах алфавита.

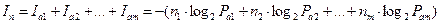
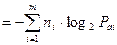(бит).

Разделив и умножив это выражение на n (n ≠ 0),приведем это выражение к виду:

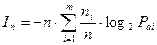(бит)

Ясно, что отношение 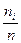– это априорная вероятность появления i-го символа. Таким образом, при достаточно большом n, имеем: 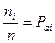, причем 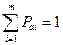, как сумма вероятностей полной группы событий.

Окончательно получим:

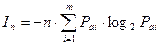(бит) (1.7)

При этом среднее количество информации, приходящееся на один символ (Н), будет равно:

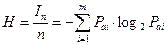
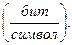(1.8)

Определенная таким образом величина Н называется энтропией, а формула (17) известна как формула Шеннона для энтропии источника дискретных сообщений. Энтропия определяет среднее количество информации, приходящееся на один символ дискретного сообщения.

В общем случае, символы, входящие в сообщения, могут появляться не только с различной вероятностью, но и быть статистически зависимыми. Статистическая зависимость может быть выражена условной вероятностью появления одного символа после другого.

Чтобы учесть статистические связи между символами, входящими в сообщение, вводят понятие условной энтропии.

Условная энтропия ( 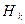) определяется выражением

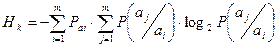
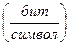, (1.9)

где 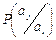– условная вероятность появления символа 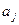после символа . Количество информации 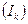, содержащееся в такого рода сообщении длиной n символов, равно:

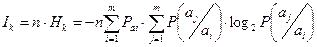(бит) (1.10)