Оценка доверительных границ при однократном наблюдении
Однократное наблюдение наиболее часто используется при проведении измерений; при этом результат однократного наблюдения Х принимают за результат измерений (здесь, конечно, необходимо ввести все поправки на условия проведения измерений, если они имеются).
Будем обозначать q(Р) – доверительные границы, обусловленные неисключенными систематическими погрешностями, а s(Х) – среднеквадратичное отклонение для величины Х, обусловленное случайными погрешностями.
Доверительные границы q(Р) определяют по формуле
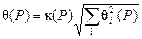 , ,
| (9.7) |
где qi – границы интервала, внутри которого находится i-я составляющая неисключенной систематической погрешности; k(Р) – коэффициент, зависящий от принятой вероятности Р. При Р = 0.9 k(Р)=0.95, при Р = 0.95 k(Р) = 1.1, а при Р = 0.99 k(Р)=1.3.
Среднеквадратичное отклонение s(Х) результата измерений вычисляют одним из следующих способов.
1). Если в технической документации на средства измерений и в методиках выполнения измерений не указаны нормально распределенные составляющие случайной погрешности, то
 , ,
| (9.8) |
где si – значение среднеквадратичного отклонения i-й составляющей погрешности. Тогда доверительная граница В(Р) случайной составляющей погрешности при заданной вероятности Р будет равна
| В(Р) = Z(Р)·s(Х), | (9.9) |
где Z(Р)=1.65 при Р = 0.9, Z(Р) = 1.96 при Р = 0.95 и Z(Р) = 2.58 при Р = 0.99.
2). Если в тех же документах случайные составляющие представлены доверительными границами Bi(Р), то
 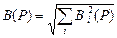 , s(Х) = B(Р)/Z(Р). , s(Х) = B(Р)/Z(Р).
| (9.10) |
3). Если случайные погрешности представлены в документах границами, соответствующими разным значениям доверительной вероятности Рi, то
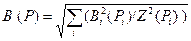 . .
| (9.11) |
Для суммирования систематической и случайной составляющих (обозначим D(Р) – границы доверительного интервала) рекомендуется следующее:
– если q(Р)/s(Х)< 0.8, то можно пренебречь систематической составляющей θ(Р) и окончательно принять D(Р) = B(Р);
– если q(Р)/s(Х) > 8, то можно пренебречь случайной составляющей и окончательно принять D(Р) = q(Р);
– если q(Р)/s(Х) в пределах от 0.8 до 8, то
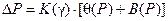 , ,
| (9.12) |
где  , , 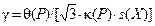 . .
| (9.13) |
Дата добавления: 2020-03-17; просмотров: 569;











