Оценка нелинейных искажений усилительных каскадов
Аналитический расчет НИ представляет собой довольно сложную задача и в полной мере может проводиться с помощью ЭВМ.
Для каскадов на БТ возможна аналитическая оценка НИ для случая малых нелинейностей ( 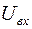 одного порядка с
одного порядка с 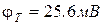 ) [15].
) [15].
Обычно уровень НИ характеризуется коэффициентом гармоник 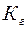 . Суммарный коэффициент гармоник равен
. Суммарный коэффициент гармоник равен
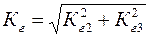 ,
,
где 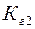 и
и 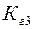 соответственно коэффициенты гармоник по второй и третьей гармоническим составляющим (составляющими более высокого порядка можно пренебречь ввиду их относительной малости).
соответственно коэффициенты гармоник по второй и третьей гармоническим составляющим (составляющими более высокого порядка можно пренебречь ввиду их относительной малости).
Коэффициенты гармоник 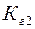 и
и 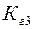 , независимо от способа включения БТ, определяются из следующих соотношений:
, независимо от способа включения БТ, определяются из следующих соотношений:
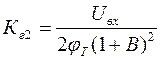 ,
,
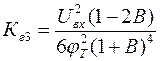 ,
,
где В - фактор связи (петлевое усиление).
Данные выражения учитывают только нелинейность эмиттерного перехода и получены на основе разложения в ряд Тейлора функции тока эмиттера 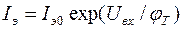
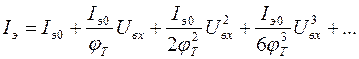 .
.
Фактор связи зависит от способа включения транзистора и вида обратной связи. Для каскада с ОЭ и ПООСТ имеем:
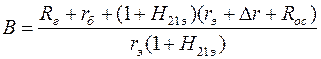 ,
,
где 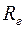 - сопротивление источника сигнала (или
- сопротивление источника сигнала (или 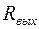 предыдущего каскада);
предыдущего каскада); 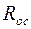 - сопротивление ПООСТ (см. подраздел 3.2, в случае отсутствия ПООСТ
- сопротивление ПООСТ (см. подраздел 3.2, в случае отсутствия ПООСТ 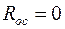 ).
).
Для каскада с ОЭ и ||ООСН
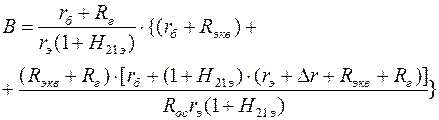 ,
,
где 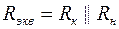 ,
, 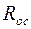 - сопротивление ||ООСН (см. подраздел 3.4).
- сопротивление ||ООСН (см. подраздел 3.4).
Для каскада с ОК
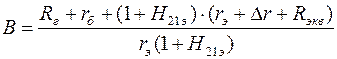 ,
,
где 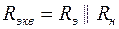 (см. подраздел 2.8).
(см. подраздел 2.8).
Для каскада с ОБ
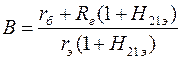 .
.
Коэффициенты гармоник 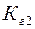 и
и 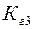 , независимо от способа включения ПТ, определяются из следующих соотношений:
, независимо от способа включения ПТ, определяются из следующих соотношений:
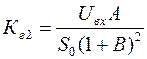 ,
,
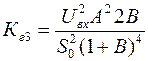 ,
,
где А - коэффициент, равный второму члену разложения выражения для нелинейной крутизны в ряд Тейлора, равный [15]
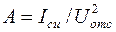 ,
,
где 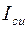 и
и 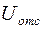 см. рисунок 2.33.
см. рисунок 2.33.
Фактор связи В зависит от способа включения транзистора и вида ООС. Для каскада с ОИ и ПООСТ имеем:
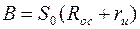 ,
,
где 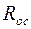 - сопротивление ПООСТ (см. подраздел 3.2, в случае отсутствия ПООСТ
- сопротивление ПООСТ (см. подраздел 3.2, в случае отсутствия ПООСТ 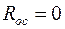 ).
).
Для каскада с ОИ и ||ООСН имеем:
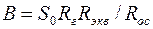 ,
,
где 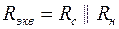 ,
, 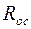 - сопротивление ||ООСН (см. подраздел 3.4).
- сопротивление ||ООСН (см. подраздел 3.4).
Для каскада с ОС
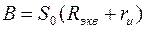 ,
,
где 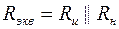 (см. подраздел 2.11).
(см. подраздел 2.11).
Для каскада с ОЗ
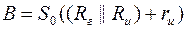 .
.
В приведенных выше выражениях 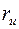 - сопротивление тела полупроводника в цепи истока,
- сопротивление тела полупроводника в цепи истока, 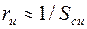 , где
, где 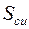 - см. подраздел 2.10, для маломощных ПТ
- см. подраздел 2.10, для маломощных ПТ 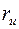 =(10…200)Ом;
=(10…200)Ом; 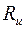 - см. рисунок 2.38.
- см. рисунок 2.38.
Приведенные соотношения для оценки 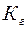 дают хороший результат в случае малых нелинейностей, в режиме больших нелинейностей следует воспользоваться известными машинными методами [4], или обратиться к графическим методам оценки НИ [6].
дают хороший результат в случае малых нелинейностей, в режиме больших нелинейностей следует воспользоваться известными машинными методами [4], или обратиться к графическим методам оценки НИ [6].
Дата добавления: 2016-06-18; просмотров: 2135;











